Bài 1 trang 118 SGK Hình học 10 nâng cao

Xét vị trí tương đối của các đường thẳng \({\Delta _1}\) và \({\Delta _2}\) trong mỗi trường hợp sau

a) \({\Delta _1}:3x - 2y + 1 = 0\) và \({\Delta _2}:2x + 3y - 5 = 0;\)

b)

\({\Delta _1}:\left\{ \matrix{
x = 4 + 2t \hfill \cr
y = - 1 + t \hfill \cr} \right.\)

 và 

\({\Delta _2}:\left\{ \matrix{
x = 7-{4t'} \hfill \cr
y = 5-{2 t'} \hfill \cr} \right.\)

c)

\({\Delta _1}:\left\{ \matrix{
x = 3 + 4t \hfill \cr
y = - 2 - 5t \hfill \cr} \right.\)

 và \({\Delta _2}:5x + 4y - 7 = 0.\)

Giải

a) Ta có \({3 \over 2} \ne \, - {2 \over 3}\) nên \({\Delta _1}\) và \({\Delta _2}\)  cắt nhau.

b) Phương trình tổng quát của \({\Delta _1}\) và \({\Delta _2}\) là

\(\eqalign{
& {\Delta _1}\,\,:\,\,x - 2y - 6 = 0 \cr
& {\Delta _2}\,\,:\,x - 2y + 3 = 0 \cr} \)

Ta có \({1 \over 1} = {{ - 2} \over { - 2}} \ne {{ - 6} \over 3}\) nên  \({\Delta _1}\) // \({\Delta _1}\)

c) Phương trình tổng quát của \({\Delta _1}\) là \(5x + 4y - 7 = 0\) . Do đó \({\Delta _1} \equiv {\Delta _2}\)

Bài 2 trang 118 SGK Hình học 10 nâng cao

Cho đường thẳng  \(\Delta :3x - 4y + 2 = 0.\)

a) Viết phương trình của Δ dưới dạng tham số.

b) Viết phương trình của Δ dưới dạng phương trình theo đoạn chắn.

c) Tính khoảng cách từ mỗi điểm \(M(3;5),N( - 4;0),P(2;1)\) tới Δ và xét xem đường thẳng  cắt cạnh nào của tam giác MNP.

d) Tính góc hợp bởi Δ và mỗi trục tọa độ.

Giải

a) Δ có vec tơ pháp tuyến là \(\overrightarrow n  = (3\,;\, - 4)\)nên có vec tơ chỉ phương là \(\overrightarrow u \left( {4;3} \right)\).

Δ đi qua điểm \(A\left( {0\,;\,{1 \over 2}} \right)\) . Vậy Δ có phương trình tham số là

\(\left\{ \matrix{
x = 4t \hfill \cr
y = {1 \over 2} + 3t \hfill \cr} \right.\)

b) Ta có  

\(3x - 4y + 2 = 0\,\,\, \Leftrightarrow \,\,\,3x - 4y =  - 2\)

\(\Leftrightarrow \,\,{x \over { - {2 \over 3}}} + {y \over {{1 \over 2}}} = 1\)

c) Ta có 

\(\eqalign{
& d(\,M\,;\,\Delta ) = {{|3.3 - 4.5 + 2|} \over {\sqrt {{3^2} + {4^2}} }} = {9 \over 5} \cr
& d(\,N\,;\,\Delta ) = {{| - 12 + 2|} \over {\sqrt {{3^2} + {4^2}} }} = {{10} \over 5} = 2 \cr
& d(\,P\,;\,\Delta ) = {{|6 - 4 + 2|} \over {\sqrt {{3^2} + {4^2}} }} = {4 \over 5} \cr} \)

M và N cùng phía đối với đường thẳng Δ còn P nằm khác  phía nên Δ không cắt MN, Δ cắt MP và NP.

d) Đường thẳng Ox có phương trình  y = 0, α là góc giữa α với Ox thì

\(\cos \alpha  = {{|3.0 - 4.1|} \over {\sqrt {{3^2} + {4^2}} .\sqrt {{0^2} + {1^2}} }} = {4 \over 5}\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Rightarrow \,\,\alpha  \approx {36^0}52'\)

Phương trình đường thẳng Oy là  x = 0, \(\beta  \) là góc giữa Δ  với Oy  ta có 

\(\cos \beta  = {{|3.1 - 4.0|} \over {\sqrt {{3^2} + {4^2}} .\sqrt {{1^2} + {0^2}} }} = {3 \over 5}\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Rightarrow \,\,\beta  \approx {53^0}7'\)

Bài 3 trang 118 SGK Hình học 10 nâng cao

Cho đường thẳng \(d:x - y + 2 = 0\) và điểm A(2, 0)

a) Với điều kiện nào của x và y thì điểm M(x, y) thuộc nửa mặt phẳng có bờ d và chứa gốc tọa độ O? Chứng minh điểm A nằm trong nửa mặt phẳng đó.

b) Tìm điểm đối xứng với điểm O qua đường thẳng d.

c) Tìm điểm M trên d sao cho chu vi tam giác OMA nhỏ nhất.

Giải

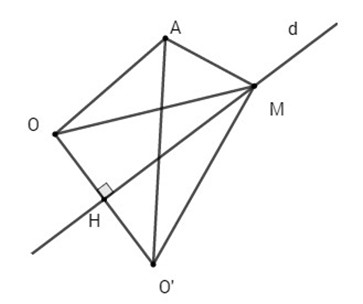
a) Điểm M và O nằm cùng phía đối với d khi và chỉ khi

\((x - y + 2).(0 - 0 + 2) > 0\,\,\, \Leftrightarrow \,\,\,x - y + 2 > 0\)

Ta có : \({x_A} - {y_A} + 2 = 2 - 0 + 2 = 4 > 0\) , do đó A nằm trong nửa mặt phẳng có bờ là d và chứa O.

b) Gọi d’ là đường thẳng qua O và vuông góc với d thì phương trình tổng quát của d’ là  \(d’: x+y=0\). Gọi H là hình chiếu của O lên d thì tọa độ H là nghiệm của hệ:

\(\left\{ \matrix{
x - y = - 2 \hfill \cr
x + y = 0 \hfill \cr} \right.\,\,\,\, \Leftrightarrow \,\,\,\left\{ \matrix{
x = - 1 \hfill \cr
y = 1 \hfill \cr} \right.\)

Vậy \(H(-1, 1)\)

Gọi O’ là điểm đối xứng của O qua d thì H là trung điểm của OO’ do đó

\(\left\{ \matrix{
{x_H} = {{{x_O} + {x_{O'}}} \over 2} \hfill \cr
{y_H} = {{{y_O} + {y_{O'}}} \over 2} \hfill \cr} \right.\,\,\,\, \Leftrightarrow \,\,\,\,\left\{ \matrix{
{x_{O'}} = 2{x_H} - {x_O} = - 2 \hfill \cr
{y_{O'}} = 2{y_H} - {y_O} = 2 \hfill \cr} \right.\) 

Vậy \(O'(-2, 2)\)

c) OA không đổi nên chu vi tam giác AMO nhỏ nhất  khi tổng MO+MA nhỏ nhất.

Ta có: \(MO = MO'\Rightarrow \,\,\,MO + MA = MO' + MA \ge \,AO'\)

\( \Rightarrow \,\,MO + MA\) nhỏ nhất khi A, M, O’ thẳng hàng , khi đó M là giao điểm của d với đường thẳng O’A.

Phương trình O’A :

\(\eqalign{
& {{x - {x_A}} \over {{x_{O'}} - {x_A}}} = {{y - {y_A}} \over {{y_{O'}} - {y_A}}} \cr
& {{x - 2} \over { - 2 - 2}} = {{y - 0} \over {2 - 0}}\,\,\,\,\, \Leftrightarrow \,\,\,x + 2y - 2 = 0 \cr} \)

Tọa độ M là nghiệm của hệ: 

\(\left\{ \matrix{
x - y = - 2 \hfill \cr
x + 2y = 2 \hfill \cr} \right.\,\,\, \Leftrightarrow \,\,\,\left\{ \matrix{
x = - {2 \over 3} \hfill \cr
y = {4 \over 3} \hfill \cr} \right.\,\,\)

Vậy \(M\left( { - {2 \over 3}\,;\,{4 \over 3}} \right)\)

Bài 4 trang 118 SGK Hình học 10 nâng cao

Cho đường thẳng \(\Delta :ax + by + c = 0\) và điểm \(I({x_0};{y_0}).\)Viết phương trình đường thẳng  đối xứng với đường thẳng Δ qua I.

Giải

Đường thẳng Δ' đối xứng với đường thẳng Δ qua  I thì Δ // Δ' do đó phương trình tổng quát của Δ' có dạng \(ax + by + c' = 0\,\,(c' \ne c)\).Ta có

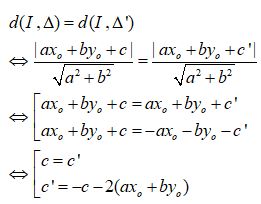
Loại trường hợp \(c=c’\).

Vậy \(\Delta '\,\,:ax + by - c - 2(a{x_o} + b{y_o} + c) = 0\)

Giaibaitap.me