Bài 12 trang 119 SGK Hình học 10 Nâng cao

Cho elip \((E):{{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1.\)

a) Xác định tọa độ hai tiêu điểm  và các đỉnh của (E).

b) Viết phương trình chính tắc của hypebol (H) nhận các tiêu điểm của (E) làm đỉnh và có hai tiêu điểm là hai đỉnh của elip (E).

c) Vẽ phác elip (E) và hypebol (H) nói ở câu b) trong cùng một hệ trục tọa độ.

d) Viết phương trình của đường tròn đi qua các giao điểm của hai đường cônic nói trên.

Giải

a) Ta có: \(a = 5\,,\,\,\,b = 3\,,\,\,c = \sqrt {{a^2} - {b^2}}  = 4\)

Tọa độ các tiêu điểm của (E) là \({F_1}\,( - 4\,;\,0)\,,\,\,{F_2}\,(4\,;\,0)\) .

Tọa độ các đỉnh của (E) là \({A_1}( - 5\,;\,0)\,,\,\,{A_2}(5\,;\,0)\,,\,\,{B_1}(0\,;\, - 3)\,,\,\,{B_2}(0\,;\,3)\) .

b) (H) nhận (-4, 0) và (4, 0) làm đỉnh thì \(a=4\).

 (H) nhận (-5, 0) và (5, 0) làm tiêu điểm  thì  có \(c=5\).

\( \Rightarrow \,\,{b^2} = {c^2} - {a^2} = 25 - 16 = 9\,\,\, \Rightarrow \,\,\,b = 3\)

Vậy phương trình chính tắc của hypebol (H) là : \({{{x^2}} \over {16}} - {{{y^2}} \over 9} = 1\)

c) Vẽ (E) và (H).

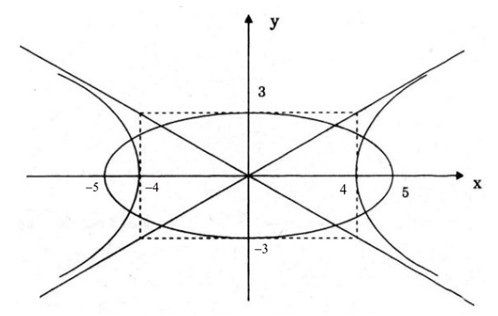
d) Tọa độ giao điểm của (E) và (H) là nghiệm của hệ phương trình

\(\left\{ \matrix{
{{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1 \hfill \cr
{{{x^2}} \over {16}} - {{{y^2}} \over 9} = 1 \hfill \cr} \right.\,\,\,\,\, \Leftrightarrow \,\,\,\left\{ \matrix{
{x^2} = {{800} \over {41}} \hfill \cr
{y^2} = {{81} \over {41}} \hfill \cr} \right.\) 

Vậy (E) và (H) cắt nhau tại 4 điểm có tọa độ thỏa phương trình \({x^2} + {y^2} = {{881} \over {41}}\)

Vậy đường tròn đi qua các giao điểm  của (E) và (H) có phương trình là \({x^2} + {y^2} = {{881} \over {41}}\)

Bài 13 trang 120 SGK Hình học 10 Nâng cao

Cho parabol \((P):{y^2} = 2px.\) Với mỗi điểm M trên (P) (M khác O), gọi M’ là hình chiếu của M trên  Oy  và  I  là trung điểm của đoạn OM’. Chứng minh rằng đường thẳng IM cắt parabol đã cho tại một điểm duy nhất.

Giải

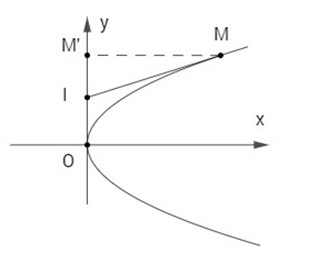
Giả sử \(M({x_o}\,;\,{y_o})\,\, \in \,\,\,(P)\)  ta có \(y_o^2 = 2p{x_o}\,({x_o} \ne 0)\) . M’ là hình chiếu của M trên Oy nên \(M'(0\,;\,{y_o})\) , khi đó \(I\left( {0\,;\,{{{y_o}} \over 2}} \right)\,\, \Rightarrow \,\,\overrightarrow {IM}  = \left( {{x_o}\,;\,{{{y_o}} \over 2}} \right)\) là vectơ chỉ phương của đường thẳng IM.

Phương trình tham số của IM là 

\(\left\{ \matrix{
x = {x_o}.t \hfill \cr
y = {{{y_o}} \over 2} + {{{y_o}} \over 2}.t \hfill \cr} \right.\)

Thay x, y trong phương trình tham số của IM vào phương trình của (P) ta được

\({{y_o^2} \over 4}(1 + {t^2}) = 2p{x_o}t\)

mà \(2p{x_o} = y_o^2\) nên \(y_o^2(1 + {t^2}) = 4y_o^2t\,\,\, \Leftrightarrow \,\,(1 + {t^2}) = 4t\,\,\) ( do \({y_o} \ne 0\)) 

\(\eqalign{
& \,\, \Leftrightarrow \,\,{(t - 1)^2} = 0\,\,\, \cr
& \,\, \Leftrightarrow \,t = 1 \cr} \)                                                       

Vậy IM cắt (P) tại điểm duy nhất \(M({x_o}\,;\,{y_o})\,\) .

Bài 14 trang 120 SGK Hình học 10 Nâng cao

Cho parabol \((P):{y^2} = {1 \over 2}x.\) Gọi M,N là hai điểm di động trên (P) sao cho \(OM \bot ON\) (M,N không trùng với O). Chứng minh rằng đường thẳng MN luôn đi qua một điểm cố định.

Giải

Giả sử \(M(2y_1^2\,;\,{y_1})\,\, \in \,\,(P)\,,\,\,N(2y_2^2\,;\,{y_2})\,\, \in \,\,(P)\) trong đó \({y_1},\,{y_2}\, \ne 0\) và \({y_1} \ne \,{y_2}\) vì \(\overrightarrow {OM} .\,\overrightarrow {ON}  = 0\) nên \(4y_1^2y_2^2 + {y_1}{y_2} = 0\)

 suy ra \(4{y_1}{y_2} + 1 = 0\,\,\, \Leftrightarrow \,\,{y_1}{y_2} =  - {1 \over 4}\)

Ta có \(\overrightarrow {MN}  = \left( {2y_2^2 - 2y_1^2\,;\,{y_2} - {y_1}} \right) \)

                    \(= \left( {{y_2} - {y_1}} \right).\left( {2{y_2} + 2{y_1}\,;\,1} \right)\)

Vì \({y_1} \ne \,{y_2}\) nên vec tơ chỉ phương của đường thẳng MN là \((2{y_1} + 2{y_2}\,;\,1)\) .

Do đó vec tơ pháp tuyến của MN là \(\overrightarrow n  = (1\,;\, - 2{y_1} - 2{y_2})\)

 Phương trình tổng quát của MN là

\(1.(x - 2y_1^2) - (2{y_1} + 2{y_2}).(y - {y_1}) = 0\)

Tìm giao điểm của MN với trục hoành bằng cách thay \(y=0\) vào (*) ta được

\(x - 2y_1^2 + 2y_1^2 + 2{y_1}{y_2} = 0\,\,\,\, \Leftrightarrow \,\,\,x = {1 \over 2}\)

Vậy MN đi qua điểm \(\left( {{1 \over 2}\,;\,0} \right)\) cố định.

Giaibaitap.me