Bài 1 trang 25 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo
Câu hỏi:
a) A = {đỏ; cam; vàng; lục; lam}, B = {lục; lam; chàm; tím}.
b) A là tập hợp các tam giác đều, B là tập hợp các tam giác cân.
a) A = {đỏ; cam; vàng; lục; lam}, B = {lục; lam; chàm; tím}.
\(A \cup B = \){đỏ; cam; vàng; lục; lam; chàm; tím}
\(A \cap B = \){lục; lam}
b) Vì mỗi tam giác đều cũng là một tam giác cân nên \(A \subset B.\)
\(A \cup B = B,\;A \cap B = A.\)
Chú ý
Nếu \(A \subset B\) thì \(A \cup B = B,\;A \cap B = A.\)
Bài 2 trang 25 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo
Câu hỏi:
Xác định các tập hợp \(A \cap B\) trong mỗi trường hợp sau:
a) \(A = \{ x \in \mathbb{R}|{x^2} - 2 = 0\} ,\)\(B = \{ x \in \mathbb{R}|2x - 1 < 0\} \)
b) \(A = \{ (x;y)|\;x,y \in \mathbb{R},y = 2x - 1\} ,\)\(B = \{ (x;y)|\;x,y \in \mathbb{R},y = - x + 5\} \)
c) A là tập hợp các hình thoi, B là tập hợp các hình chữ nhật.
a) \(A \cap B = \{ x|x \in A\) và \(x \in B\} \)
b) \(A \cap B = \{ (x;y)|\;x,y \in \mathbb{R},y = 2x - 1,y = - x + 5\} \)
a) Phương trình \({x^2} - 2 = 0\) có hai nghiệm là \(\sqrt 2 \) và \( - \sqrt 2 \), nên \(A = \{ \sqrt 2 ; - \sqrt 2 \} \)
Tập hợp \(B = \{ x \in \mathbb{R}|2x - 1 < 0\} \) là tập hợp các số thực \(x < \frac{1}{2}\)
Từ đó \(A \cap B = \{ - \sqrt 2 \} .\)
b) \(A \cap B = \{ (x;y)|\;x,y \in \mathbb{R},y = 2x - 1,y = - x + 5\} \)
Tức là \(A \cap B\)là tập hợp các cặp số (x; y) thỏa mãn hệ phương trình: \(\left\{ \begin{array}{l}y = 2x - 1\\y = - x + 5\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}2x - 1 = - x + 5\\y = 2x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x = 6\\y = 2x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3\end{array} \right.\)
Vậy \(A \cap B = \{ (2;3)\} .\)
c) A là tập hợp các hình thoi, B là tập hợp các hình chữ nhật.
\(A \cap B\) là tập hợp các hình vừa là hình chữ nhật vừa là hình thoi.
Một tứ giác bất kì thuộc \(A \cap B\) thì nó là hình chữ nhật và có 2 cạnh kề bằng nhau (hình vuông)
Do đó \(A \cap B\) là tập hợp các hình vuông.
Bài 3 trang 25 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo
Câu hỏi:
Cho \(E = \{ x \in \mathbb{N}|x < 10\} ,A = \{ x \in E|x\)là bội của 3\(\} ,\)\(B = \{ x \in E|x\) là ước của 6\(\} .\)
Xác định các tập hợp \(A\backslash B,{\rm{ }}B\backslash A,\;{C_E}A,\;{C_E}B,{C_E}(A \cup B),{C_E}(A \cap B).\)
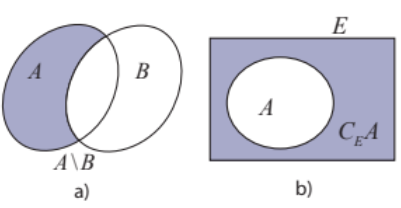
\(E = \{ x \in \mathbb{N}|x < 10\} = \{ 0;1;2;3;4;5;6;7;8;9\} \)
\(A = \{ x \in E|x\) là bội của 3\(\} \)\( = \{ 0;3;6;9\} \)
\(B = \{ x \in E|x\) là ước của 6\(\} \)\( = \{1;2;3;6\} \)
Ta có: \(A\backslash B = \left\{ {0;9} \right\}\), \(B\backslash A = \left\{ {1;2} \right\}\)
\({C_E}A = \{ 1;2;4;5;7;8\} ,\;{C_E}B = \{ 0;4;5;7;8;9\} \)
\(A \cap B = \{ 3;6\} \Rightarrow {C_E}(A \cap B) = {C_E}B = \{0;1;2;4;5;7;8;9\} \)
\(A \cup B = \{ 0;1;2;3;6;9\} \Rightarrow {C_E}(A \cup B) = {C_E}A = \{ 4;5;7;8\} \)
Bài 4 trang 25 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo
Câu hỏi:
Cho A và B là hai tập hợp bất kì. Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập hợp còn lại? Hãy
giải thích bằng cách sử dụng biểu đồ Ven.
a) A và \(A \cup B\)
b) A và \(A \cap B\)
Ta có sơ đồ ven sau:
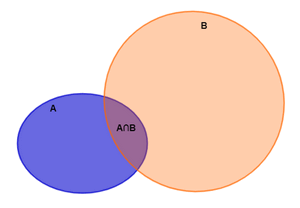
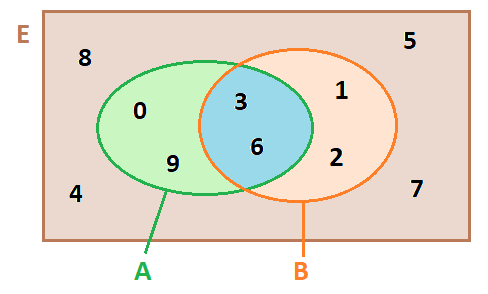
Ta thấy tập hợp A ∪ B bao gồm phần màu xanh, phần màu tím và phần màu cam.
Tập hợp A chứa phần màu xanh cộng màu tím nằm hoàn toàn trong tập hợp A ∪ B. Do đó tập A là tập con của
tập A ∪ B. Ta viết A ⊂ (A∪B).
Tập hợp A∩B là phần màu tím và nằm hoàn toàn trong tập hợp A nên tập A∩B là tập con của tập A. Ta viết (A∩B) ⊂ A.
Bài 5 trang 25 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo
Câu hỏi:
Trong số 35 học sinh của lớp 10H, có 20 học sinh thích học môn Toán, 16 học sinh thích môn Tiếng Anh và 12 học sinh thích cả hai môn này. Hỏi lớp 10H:
a) có bao nhiêu học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh?
b) có bao nhiêu học sinh không thích cả hai môn này?
Phương pháp:
Kí hiệu A, B lần lượt là tập hợp các học sinh thích môn Toán và Tiếng Anh.
Sử dụng biểu đồ Ven, minh họa tập hợp các thích ít nhất một trong hai môn Toán và Tiếng Anh (\(A \cup B\)) và các học sinh không thích cả hai môn này.
Ta có sơ đồ ven:
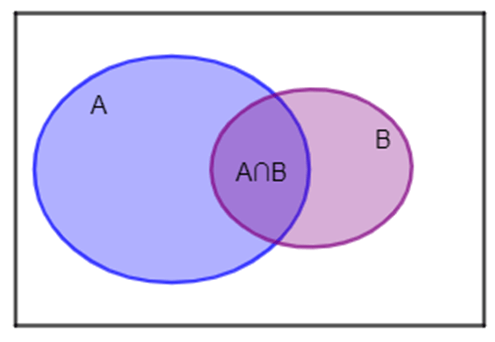
a) Gọi A là tập hợp học sinh của lớp 10H thích học môn Toán, B là tập hợp học sinh của lớp 10H thích học môn Tiếng Anh.
Theo giả thiết, n(A) = 20, n(B) = 16, n(A∩B) = 12.
Nhận thấy rằng, nếu tính tổng n(A) + n(B) thì ta được số học sinh lớp 10H thích môn Toán hoặc Tiếng Anh, nhưng số bạn thích cả hai môn được tính hai lần. Do đó, số bạn học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh là:
n(A∪B) = n(A) + n(B) – n(A∩B) = 20 + 16 – 12 = 24.
Vậy lớp 10H có 24 học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh.
b) Số học sinh của lớp 10H không thích cả hai môn Toán và Tiếng Anh là:
35 – 24 = 11 (học sinh).
Vậy có 11 học sinh của lớp 10H không thích cả hai môn Toán và Tiếng Anh.
Bài 6 trang 25 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo
Câu hỏi:
Xác định các tập hợp sau đây:
a) \(( - \infty ;0] \cup [ - \pi ;\pi ]\)
b) \([ - 3,5;2] \cap ( - 2;3,5)\)
c) \(( - \infty ;\sqrt 2 ] \cap [1; + \infty )\)
d) \(( - \infty ;\sqrt 2 ]{\rm{\backslash }}[1; + \infty )\)
Biểu diễn các tập hợp trên trục số
Trả lời:
a) Ta có: (– ∞; 0] = {x thuộc R| x ≤ 0} và [– π; π] = {x thuộc R| – π ≤ x ≤ π}
-> (– ∞; 0] ∪ [– π; π] = {x thuộc R| x ≤ 0 hoặc – π ≤ x ≤ π} = {x thuộc R| x ≤ π} = [– ∞; π] .
Vậy (– ∞; 0] ∪ [– π; π] = [– ∞; π] .
b) Ta có: [– 3,5; 2] = {x thuộc R| – 3,5 ≤ x ≤ 2} và (– 2; 3,5) ={x thuộc R| – 2 < x < 3,5}
-> [– 3,5; 2] ∩ (– 2; 3,5) = {x thuộc R| – 3,5 ≤ x ≤ 2, – 2 < x < 3,5} = {x thuộc R| – 2 < x ≤ 2} = (– 2; 2].
Vậy [– 3,5; 2] ∩ (– 2; 3,5) = (– 2; 2].
c) Ta có (– ∞; căn 2] = {x thuộc R| x ≤ căn 2} và [1; +∞) = {x thuộc R| x ≥ 1}.
-> (– ∞; căn 2] ∩ [1; +∞) = {x thuộc R| x ≤ căn 2, x ≥ 1} = {x thuộc R| 1 ≤ x ≤ căn 2 căn 2]
Vậy (– ∞; căn 2] ∩ [1; +∞) = [1; căn 2].
d) Ta có (– ∞; căn 2] = {x thuộc R| x ≤ căn 2} và [1; +∞) = {x thuộc R| x ≥ 1}
-> (– ∞; căn 2] \ [1; +∞) = {x thuộc R| x ≤ căn 2} nhưng không thỏa mãn x ≥ 1} = {x thuộc R| x < 1} = (– ∞; 1).
Vậy (– ∞; căn 2] \ [1; +∞) = (– ∞; 1).
Giaibaitap.me
Giải bài tập trang 27 Bài tập cuối chương 1 - SGK Toán 10 tập 1 Chân trời sáng tạo. Bài 1 : Xác định tính đúng sai của mỗi mệnh đề sau:
Giải bài tập trang 32 - SGK Toán 10 tập 1 Chân trời sáng tạo - Bài 1: Bất phương trình bậc nhất hai ẩn. Bài 1 : Cho bất phương trình bậc nhất hai ẩn x - 2y + 6 > 0. a) (0 ; 0) có phải là một nghiệm của bất phương trình đã cho không ?
Giải Toán 10 trang 37, 38 Chân trời sáng tạo tập 1 - Bài 2: Hệ bất phương trình bậc nhất hai ẩn. Bài 2 : Một nhà máy sản xuất hai loại thuốc trừ sâu nông nghiệp là A và B. Cứ sản xuất mỗi thùng loại A thì nhà máy thải ra 0,25 kg khí cacbon dioxide
Giải bài tập Toán 10 trang 39 Chân trời sáng tạo tập 1 - Bài tập cuối chương 2. Bài 1 : Biểu diễn miền nghiệm của mỗi bất phương trình sau trên mặt phẳng tọa độ Oxy.
