Bài 1 trang 86 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo

Câu hỏi:

a) Bạn hãy tìm sự khác biệt giữa hai đại lượng sau:

- Bác Ba có số tiền là 20 triệu đồng.

- Một cơn bão di chuyển với vận tốc 20 km/h theo hướng đông bắc.

b) Trong các đại lượng sau, đại lượng nào cần được biểu diễn bởi vectơ?

Giá tiền, lực, thể tích, tuổi, độ dịch chuyển, vận tốc.

Trả lời: 

a) Sự khác biệt giữa hai đại lượng đã cho là:

- Bác Ba có số tiền là 20 triệu đồng, đại lượng này là một đại lượng vô hướng vì nó chỉ số tiền nên nó chỉ có độ lớn.

- Một cơn bão di chuyển với vận tốc 20 km/h theo hướng đông bắc, đại lượng này là một đại lượng có hướng vì nó có đề cập đến độ lớn và hướng.

b) Trong các đại lượng đã cho, các đại lượng lực, độ dịch chuyển, vận tốc là các đại lượng có hướng, chúng bao gồm cả độ lớn và hướng nên các đại lượng đó cần được biểu diễn bởi vectơ.

Bài 2 trang 86 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo

Câu hỏi:

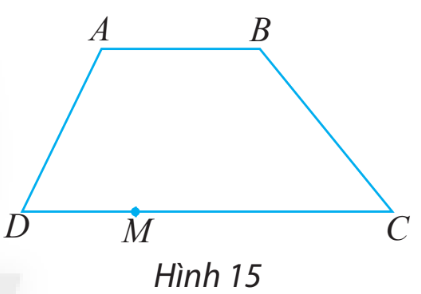
Cho hình thang ABCD có hai cạnh đáy là AB và DC (hình 15). Điểm M nằm trên đoạn DC.

a) Gọi tên các vectơ cùng hướng với vectơ \(\overrightarrow {AB} \)

b) Gọi tên các vectơ ngược hướng với vectơ \(\overrightarrow {DM} \)

Phương pháp: 

a) Bước 1: Từ h15 tìm các cạnh song song hoặc trùng với cạnh AB

Bước 2: Trong đó, chỉ ra các vectơ có hướng từ trái qua phải.

b) Bước 1: Từ h15 tìm các cạnh song song hoặc trùng với cạnh DM

Bước 2: Trong đó, chỉ ra các vectơ có hướng từ trái qua phải.

Trả lời: 

a) ABCD là hình thang nên AB//CD

Các vectơ cùng hướng với vectơ \(\overrightarrow {AB} \) là các vectơ có hướng từ trái qua phải nên đó là: \(\overrightarrow {DC} ,\overrightarrow {DM} ,\overrightarrow {MC} \)

b) \(\overrightarrow {DM} \)có hướng từ trái sang phải nên các vectơ ngược hướng với vectơ \(\overrightarrow {DM} \)là \(\overrightarrow {BA} ,\overrightarrow {MD} ,\overrightarrow {CM} ,\overrightarrow {CD} \)

Bài 3 trang 86 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo

Câu hỏi:

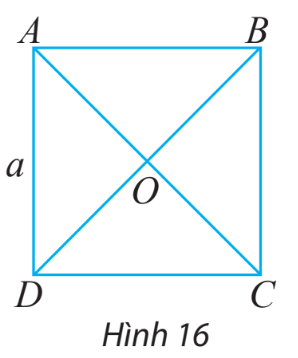
Cho hình vuông ABCD có tâm O và có các cạnh bằng a (hình 16)

a)  Tìm trong hình hai vectơ bằng nhau và có độ dài bằng \(\frac{{a\sqrt 2 }}{2}\)

b)  Tìm trong hình hai vectơ đối nhau và có độ dài bằng \(a\sqrt 2\)

Phương pháp: 

a) Bước 1: Tìm độ dài các cạnh \(AB,BC,CD,DA,AC,BD...\)

Bước 2: Xác định hướng của các vectơ có độ dài bằng \(\frac{{a\sqrt 2 }}{2}\)

Bước 3: Từ bước 2, chỉ ra hai vectơ cùng hướng

Trả lời: 

a)  \(AC = BD = \sqrt {A{D^2} + D{C^2}}  = \sqrt {{a^2} + {a^2}}  = a\sqrt 2 \)

\( \Rightarrow AO = OC = BO = OD = \frac{{a\sqrt 2 }}{2}\)

Suy ra các cặp vectơ bằng nhau và có độ dài bằng \(\frac{{a\sqrt 2 }}{2}\) là:

\(\overrightarrow {AO} \)và \(\overrightarrow {OC} \); \(\overrightarrow {CO} \) và \(\overrightarrow {OA} \); \(\overrightarrow {DO} \) và \(\overrightarrow {OB} \); \(\overrightarrow {OD} \) và \(\overrightarrow {BO} \)

b) Trong hình chỉ có 2 đoạn thẳng AC và BD có độ dài là \(a\sqrt 2\).

Do đó hai vectơ đối nhau và có độ dài bằng \(a\sqrt 2\) là: 

\(\overrightarrow {AC} \)và \(\overrightarrow {CA} \); \(\overrightarrow {BD} \) và \(\overrightarrow {DB} \).

Bài 4 trang 86 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo

Câu hỏi:

Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi \(\overrightarrow {AB}  = \overrightarrow {DC} \)

Phương pháp: 

\(\overrightarrow {AB}  = \overrightarrow {DC} \) nếu 

+ \(\overrightarrow {AB}  ,\, \overrightarrow {DC} \) cùng hướng

+ \(AB =CD\)

Trả lời: 

Tứ giác ABCD là hình bình hành 

\( \Leftrightarrow \left\{ \begin{array}{l}
AB // DC\\
AB = DC
\end{array} \right.\)

Mà \(AB // DC \Leftrightarrow \overrightarrow {AB}  ,\, \overrightarrow {DC} \) cùng phương, do đó cùng hướng.

\( \Leftrightarrow \left\{ \begin{array}{l}
\overrightarrow {AB} , \overrightarrow {DC} \,{\rm{ cùng hướng}}\\
AB = DC
\end{array} \right.\)

\(\Leftrightarrow \overrightarrow {AB}  = \overrightarrow {DC} \)

Vậy tứ giác ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {AB}  = \overrightarrow {DC} \).

Bài 5 trang 86 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo

Câu hỏi:

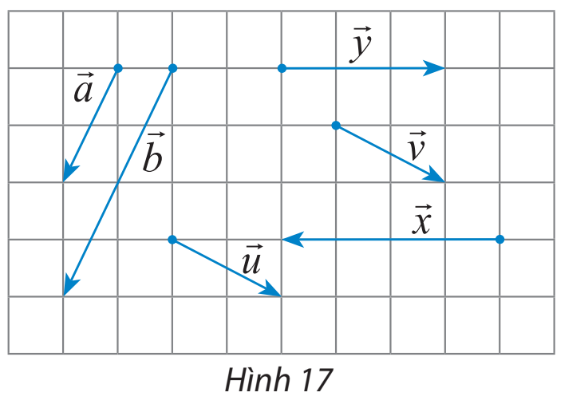
Hãy chỉ ra các cặp vectơ cùng hướng, ngược hướng, bằng nhau trong hình 17.

Phương pháp: 

Bước 1: Xác định các vecto có giá song song hoặc trùng nhau

Bước 2: Xác định hướng của các vectơ => Kết luận các cặp vecto cùng hướng, ngược hướng.

Bước 3: So sánh độ dài của các cặp vecto cùng hướng => Kết luận các cặp vecto bằng nhau

Trả lời: 

+ Các cặp vectơ cùng hướng là: \(\overrightarrow a \) và \(\overrightarrow b \); \(\overrightarrow u \) và \(\overrightarrow v \)

+ Các cặp vectơ ngược hướng là: \(\overrightarrow x \) và \(\overrightarrow y \)

+ Các cặp vectơ bằng nhau là: \(\overrightarrow u \) và \(\overrightarrow v \)

Bài 6 trang 87 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo

Câu hỏi:

Gọi O là tâm hình lục giác đều ABCDEF.

a) Tìm các vectơ khác vectơ \(\overrightarrow 0 \) và cùng hướng với vectơ \(\overrightarrow {OA} \).

b) Tìm các vectơ bằng vectơ \(\overrightarrow {AB} \).

Phương pháp: 

a)

Bước 1: Xác định các cạnh song song hoặc trùng với cạnh OA

Bước 2: Chỉ ra các vectơ cùng hướng với vectơ \(\overrightarrow {OA} \)

b) 

Bước 1: Xác định các cạnh song song hoặc trùng cạnh AB

Bước 2: Chỉ ra các vectơ có cùng hướng với vectơ \(\overrightarrow {AB} \)

Bước 3: Trong đó, kết luận các vectơ có độ dài bằng cạnh AB

Trả lời: 

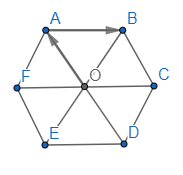
a) Ta có: AO // BC // EF

Suy ra các vectơ khác vectơ khác vectơ \(\overrightarrow 0 \) và cùng hướng với vectơ \(\overrightarrow {OA} \) là : \(\overrightarrow {DO} ,\overrightarrow {DA} ,\overrightarrow {CB} ,\overrightarrow {EF} \)

b) Ta có: \(OA = OB = OC = OD = OE = FO\) và AB // FC // ED

Suy ra các vectơ bằng vectơ \(\overrightarrow {AB} \) là \(\overrightarrow {FO} ,\overrightarrow {OC} ,\overrightarrow {ED} \)

Bài 7 trang 87 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo

Câu hỏi:

Tìm các lực cùng hướng và ngược hướng trong số các lực đẩy được biểu diễn bằng các vectơ trong hình 18

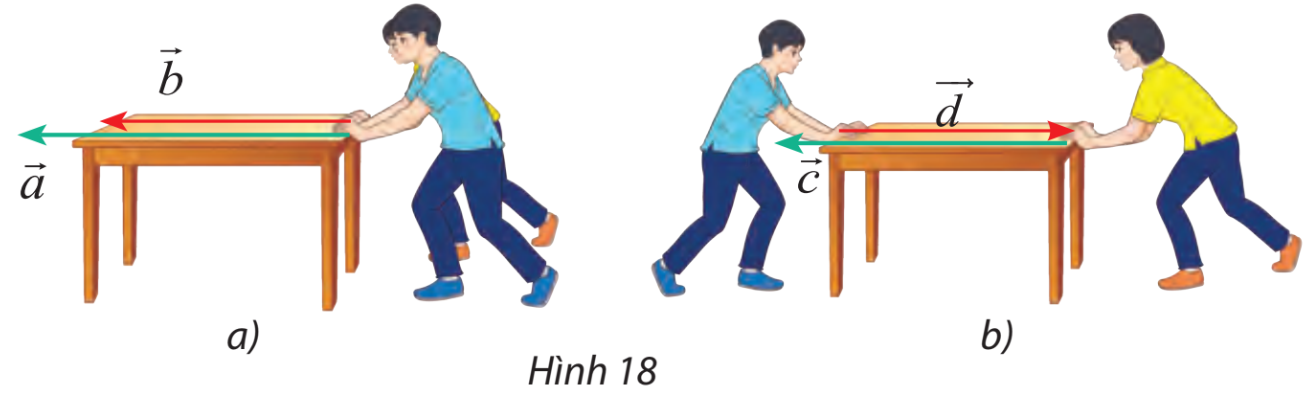
Trả lời: 

Nhận xét: giá của 4 lực đều song song hoặc trùng nhau, do đó 4 vecto là cùng phương.

Vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) có chiều từ phải sang trái còn vectơ \(\overrightarrow d \) có chiều từ trái sang phải

Vậy các vectơ (hay lực) cùng hướng với nhau là vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \).

Các vectơ (lực)  \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) ngược hướng với vectơ \(\overrightarrow d \).

Giaibaitap.me