Vì hàng lớn nhất của độ chính xác d = 100 là hàng trăm, nên ta quy tròn đến hàng nghìn. Do đó số quy tròn của số gần đúng a = 6547 là số 7000.

Sai số tương đối là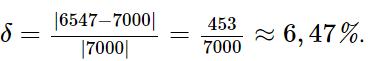 

Bài 3 trang 109 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo

Câu hỏi:

Cho biết \(\sqrt 3  = 1,7320508...\)

a) Hãy quy tròn \(\sqrt 3 \) đến hàng phần trăm và ước lượng sai số tương đối

b) Hãy tìm số gần đúng của \(\sqrt 3 \) với độ chính xác 0,003.

c) Hãy tìm số gần đúng của \(\sqrt 3 \) với độ chính xác đến hàng phần chục nghìn.

Phương pháp: 

a) Bước 1: Quy tròn số, tìm sai số tuyệt đối

Bước 2: Ước lượng sai số tương đối

b) Bước 1: Tìm hàng của chữ số khác 0 đầu tiên bên trái của d=0,003

Bước 2: Quy tròn \(\overline a  = \sqrt 3  = 1,7320508...\) đến hàng tìm được ở trên

Trả lời: 

a) Quy tròn số \(\overline a  = \sqrt 3 \) đến hàng phần trăm, ta được số gần đúng là \(a = 1,73\)

Do \(a < \overline a  < 1,735\) nên sai số tuyệt đối là

\({\Delta _a} = \left| {\overline a  - a} \right| < 0,005.\)

Sai số tương đối là \({\delta _a} \le \frac{{0,005}}{{1,73}} \approx 0,3\% \)

b) Hàng của chữ số khác 0 đầu tiên bên trái của d=0,003 là hàng phần nghìn.

Quy tròn \(\overline a \) đến hàng phần nghìn ta được số gần đúng của \(\overline a \) là \(a = 1,732\).

c) Độ chính xác đến hàng phần chục nghìn

Quy tròn \(\overline a \) đến hàng phần chục nghìn ta được số gần đúng của \(\overline a \) là \(a = 1,7321\).

Bài 4 trang 109 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo

Câu hỏi:

Hãy viết số quy trong gần đúng trong những trường hợp sau:

a) \(4536002 \pm 1000\)

b) \(10,05043 \pm 0,002\)

Phương pháp: 

Bước 1: Xác định a và d trong số đúng \(a \pm d\)

Bước 2: Tìm hàng của chữ số khác 0 đầu tiên bên trái của d

Bước 3: Quy tròn số a ở hàng gấp 10 lần hàng tìm được.

Trả lời: 

a) 4536002 ± 1000

Hàng lớn nhất của độ chính xác d = 1000 là hàng nghìn, nên ta quy tròn đến hàng phần chục nghìn.

Vậy số quy tròn trong trường hợp này là 4540000.

b) 10,05043 ± 0,002

Hàng lớn nhất của độ chính xác d = 0,002 là hàng phần nghìn, nên ta quy tròn đến hàng phần trăm.

Vậy số quy tròn cần tìm là 10,05.

Bài 5 trang 109 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo

Câu hỏi:

Một tam giác có ba cạnh đo được như sau: \(a = 5,4\;cm \pm 0,2\;cm;\;b = 7,2\;cm \pm 0,2\;cm\) và \(c = 9,7\;cm \pm 0,1\;cm\). Tính chu vi của tam giác đó.

Trả lời: 

Chu vi của tam giác là:

P = a + b + c = (5,4 ± 0,2) + (7,2 ± 0,2) + (9,7 ± 0,1)

= (5,4 + 7,2 + 9,7) ± (0,2 + 0,2 + 0,1)

= 22,3 ± 0,5  (cm).

Vậy chu vi của tam giác đã cho là P = 22,3 cm ± 0,5 cm.

Bài 6 trang 109 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo

Câu hỏi:

Chiếc kim màu đỏ chỉ cân nặng của bác Phúc (Hình 5). Hãy viết cân nặng của bác Phúc dưới dạng số gần đúng với độ chính xác 0,5 kg.

Trả lời: 

Quan sát Hình 5 ta thấy chiếc kim màu đỏ nằm giữa hai vạch 63 và 64, nghĩa là cân nặng của bác Phúc khoảng 63,5 kg.

Vậy cân nặng của bác Phúc là 63,5 ± 0,5 kg.

Giaibaitap.me