Bài 8.14 trang 75 SGK Toán 8 Kết nối tri thức tập 2

Gieo một con xúc xắc cân đối. Tính xác xuất của biến cố sau:

a) A: "Số chấm xuất hiện trên con xúc xắc khác 6"

b) B: "Số chấm xuất hiện trên con xúc xắc bé hơn 3"

c) C: "Số chấm xuất hiện trên con xúc xắc lớn hơn 2"

d) D: "Số chấm xuất hiện trên con xúc xắc là số nguyên tố"

Lời giải:

Có 6 kết quả có thể, đó là 1; 2; 3; 4; 5; 6. Các kết quả có thể này là đồng khả năng

a) Có 5 kết quả thuận lợi cho biến cố A là: 1; 2; 3; 4; 5. 

Vậy \(P(A) = \frac{5}{6}\)

b) Có 2 kết quả thuận lợi cho biến cố B là: 1; 2

Vậy \(P(B) = \frac{2}{6} = \frac{1}{3}\)

c) Có 4 kết quả thuận lợi cho biến cố C là: 3; 4; 5; 6

Vậy \(P(C) = \frac{4}{6} = \frac{2}{3}\)

d) Có 3 kết quả thuận lợi cho biến cố D là: 2; 3; 5

Vậy \(P(D) = \frac{3}{6} = \frac{1}{2}\)

Bài 8.15 trang 75 SGK Toán 8 Kết nối tri thức tập 2

Một túi đựng các quả bóng giống hệt nhau, chỉ khác màu, trong đó có 15 quả bóng màu xanh, 13 quả bóng màu đỏ và 17 quả bóng màu trắng. Lẫy ngẫu nhiên một quả bóng từ trong túi. Tính xác suất của các biến cố sau:

a) C: "Lấy được quả bóng màu xanh"

b) D: "Lấy được quả bóng màu đỏ"

c) E: "Không lấy được quả bóng màu trắng" 

Lời giải:

Có 15 quả bóng màu xanh, 13 quả bóng màu đỏ và 17 quả bóng màu trắng nên có tất cả 15 + 13 + 17 = 45 quả bóng, vậy có 45 kết quả có thể. Các kết quả có thể này là đồng khả năng do lấy ngẫu nhiên một quả bóng từ trong túi.

a) Có 15 quả bóng màu xanh nên có 15 kết quả thuận lợi cho biến cố C.

Vậy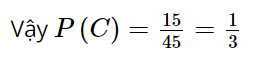 

b) Có 13 quả bóng màu đỏ nên có 13 kết quả thuận lợi cho biến cố D.
Vậy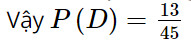 

c) Không lấy được quả bóng màu trắng, tức là lấy được bóng màu xanh hoặc màu đỏ. Tổng số quả bóng màu xanh và màu đỏ là 15 + 13 = 28 quả bóng. Do đó, có 28 kết quả thuận lợi cho biến cố E.

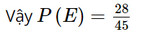
Bài 8.16 trang 75 SGK Toán 8 Kết nối tri thức tập 2

Trong trò chơi "Xúc xắc may mắn" ở mỗi ván chơi, người chơi gieo đồng thời hai con xúc xắc và ghi lại tổng số chấm xuất hiện trên hai con xúc xắn. Một người chơi 80 ván và ghi lại kết quả trong bảng sau:

a) Giả sử người chơi thắng nếu tổng số chấm xuất hiện trên hai con xúc xắc là 5 hoặc 7. Tính xác suất thực nghiệm của biến cố E: "Người chơi thắng trong một ván chơi"

b) Giả sử người chơi thắng nếu tổng số chấm xuất hiện trên hai con xúc xắc từ 10 trở lên. Tính xác suất thực nghiệm của biến cố F: "Người chơi thắng trong một ván chơi"

Lời giải:

a) Có 22 ván người chơi gieo được tổng số chấm là 5 hoặc 7 

Vậy xác suất thực nghiệm của biến cố E là \(\frac{{22}}{{80}} = 0,275\)

b) Có 13 ván người chơi gieo được tổng số chấm từ 10 trở lên

Vậy xác suất thực nghiệm của biến cố F là \(\frac{13}{{80}} =0,1625\)

Bài 8.17 trang 75 SGK Toán 8 Kết nối tri thức tập 2

Thống kê số vụ tai nạn giao thông trong hai tháng 8 và 9 của thành phố X được kết quả như bảng sau:

Từ bảng thống kê trên, hãy dự đoán xem trong ba tháng 10; 11; 12 tới tại thành phố X:

a) Có bao nhiêu ngày có nhiều nhất 3 vụ tai nạn giao thông

b) Có bao nhiêu ngày có ít nhất 5 vụ tai nạn giao thông 

Lời giải:

Tháng 8 và tháng 9 có tổng là 61 ngày.

Ba tháng 10, 11, 12 có tổng 92 ngày.

a) Có 4 + 9 + 15 + 10 = 38 ngày có từ 3 vụ tai nạn giao thông trở xuống, tức là có 38 ngày trong hai tháng 8 và 9 có nhiều nhất 3 vụ tai nạn giao thông.

Gọi E là biến cố: “Trong một ngày có nhiều nhất 3 vụ tai nạn giao thông”.

Vậy ta dự đoán số ngày có nhiều nhất 3 vụ tai nạn giao thông trong ba tháng 10, 11, 12 khoảng 57 ngày.

b) Có 6 + 4 + 3 + 2 = 15 ngày có từ 5 vụ tai nạn trở lên trong hai tháng 8 và 9.

Gọi F là biến cố: “Trong một ngày có ít nhất 5 vụ tai nạn giao thông”.

Vậy ta dự đoán số ngày có ít nhất 5 vụ tai nạn giao thông trong ba tháng 10, 11, 12 khoảng 23 ngày.

Giaibaitap.me