Bài 3.25 trang 66 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Bằng ê ke, nêu cách kiểm tra một tứ giác có là hình chữ nhật hay không. Hãy giải thích kết quả.

Phương pháp:

Dùng ê ke đo 4 góc của tứ giác ABCD 

Lời giải:

Dùng ê ke kiểm tra bốn góc của tứ giác đó:

• Nếu bốn góc của tứ giác đều là góc vuông thì tứ giác đó là hình chữ nhật.

Tuy nhiên, vì tổng bốn góc của tứ giác bằng 360° nên nếu ba góc của một tứ giác là góc vuông thì tứ giác đó có bốn góc là góc vuông, do đó tứ giác này là hình chữ nhật.

 Dùng ê ke kiểm tra được ba góc của tứ giác là góc vuông thì tứ giác đó là hình chữ nhật.

• Nếu bốn góc của tứ giác có ít nhất một góc không vuông thì tứ giác đó không là hình chữ nhật.

Giải thích: Hình chữ nhật là tứ giác có bốn góc vuông.

Bài 3.26 trang 66 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Bằng compa, nêu cách kiểm tra một tứ giác có là hình chữ nhật hay không. Hãy giải thích kết quả.

Phương pháp:

Dùng compa kiểm tra các cặp đối của tứ giác và các đường chéo của tứ giác có bằng nhau hay không?

Lời giải:

Ta kiểm tra xem các cặp đối của tứ giác:

• Nếu các cặp cạnh đối không bằng nhau thì tứ giác đó không là hình bình hành nên cũng không là hình chữ nhật.

• Nếu các cặp cạnh đối bằng nhau thì tứ giác đó là hình bình hành.

Sau đó ta kiểm tra xem hai đường chéo của tứ giác (là hình bình hành) đó.

• Nếu hai đường chéo của hình bình hành đó bằng nhau thì tứ giác đó là hình chữ nhật.

• Nếu hai đường chéo của hình bình hành đó không bằng nhau thì tứ giác đó không là hình chữ nhật.

Bài 3.27 trang 66 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Cho tam giác ABC, đường cao AH. Gọi M là trung điểm của AC, N là điểm sao cho M là trung điểm của HN. Chứng minh tứ giác AHCN là hình chữ nhật.

Phương pháp:

Chứng minh tứ giác AHCN là hình bình hành có \(\widehat {AHC} = {90^o}\) nên AHCN là hình chữ nhật 

Lời giải:

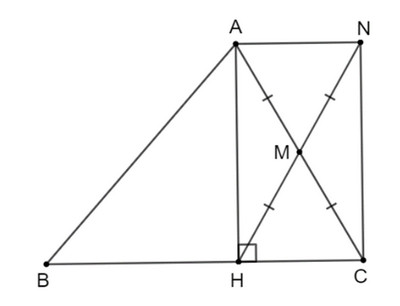
Theo đề bài, M là trung điểm của AC, N là điểm sao cho M là trung điểm của HN.

Nên tứ giác ANCH có hai đường chéo AC và HN cắt nhau tại trung điểm M của mỗi đường.

Suy ra tứ giác ANCH là hình bình hành.

Hình bình hành ANCH có \(\widehat {AHC} = {90^o}\) nên tứ giác ANCH là hình chữ nhật.

Bài 3.28 trang 66 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Xét một điểm M trên cạnh huyền của tam giác ABC vuông cân tại A. Gọi N và P lần lượt là hình chiếu vuông góc của M trên các cạnh AB và AC.

a) Hỏi tứ giác MPAN là hình gì?

b) Hỏi M ở vị trí nào thì đoạn thẳng NP có độ dài ngắn nhất? Vì sao?

Phương pháp:

a) Xét tứ giác APMN có 3 góc vuông nên là hình chữ nhật.

b) Sử dụng tính chất của hình chữ nhật.

Lời giải: 

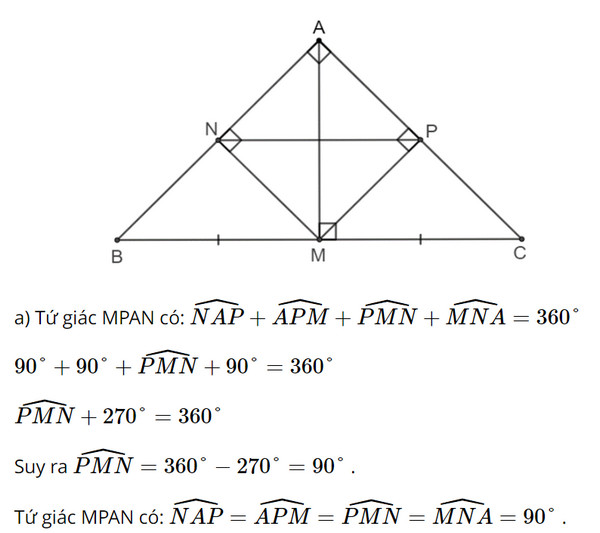
Do đó tứ giác MPAN là hình chữ nhật.

b) Vì tứ giác MPAN là hình chữ nhật có hai đường chéo AM và NP nên AM = NP.

Để đoạn thẳng NP có độ dài ngắn nhất thì AM có độ dài ngắn nhất.

Mà tam giác ABC vuông cân tại A nên AM cũng là đường trung tuyến.

Do đó M là trung điểm của BC.

Vậy M là trung điểm của đoạn thẳng BC thì đoạn thẳng NP có độ dài ngắn nhất.

Giaibaitap.me