Bài 1 trang 52 SGK Toán 8 Chân trời sáng tạo tập 1

a) Tính diện tích xung quanh của mỗi hình chóp tứ giác đều dưới đây.

b) Cho biết chiều cao của hình chóp tứ giác đều trong Hình 9a và Hình 9b lần lượt là 4cm và \(12\)cm. Tính thể tích của mỗi hình.

Lời giải:

a) Diện tích xung quanh của hình chóp trong hình 9a là: \(\frac{{6.4}}{2}.5 = 60\) (\(c{m^2}\))

Diện tích xung quanh của hình chóp trong hình 9b là: \(\frac{{10.4}}{2}.13 = 260\) (\(c{m^2}\))

b) Thể tích của hình chóp trong hình 9a là: \(\frac{1}{3}{.6^2}.4 = 48\) (\(c{m^3}\))

Thể tích của hình chóp trong hình 9b là: \(\frac{1}{3}{.10^2}.12 = 400\) (\(c{m^3}\))

Bài 2 trang 53 SGK Toán 8 Chân trời sáng tạo tập 1

Nhân dịp Tết Trung thu, Nam dự định làm một chiếc lồng đèn hình chóp tứ giác đều có độ dài cạnh đáy và đường cao của mặt bên tương ứng với cạnh đáy lần lượt là \(30\)cm và \(40\)cm. Em hãy giúp Nam tính xem phải cần bao nhiêu mét vuông giấy vừa đủ để dán tất cả các mặt của lồng đèn. Biết rằng nếp gấp không đáng kể.

Lời giải:

Diện tích giấy dán bốn mặt bên (diện tích xung quanh) của chiếc lồng đèn hình chóp tứ giác đều là:

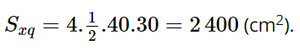
Diện tích giấy dán mặt đáy của chiếc lồng đèn hình chóp tứ giác đều là:

S_đáy = 30² = 600 (cm²).

Diện tích giấy dán tất cả các mặt (diện tích toàn phần) của chiếc lồng đèn là:

S_tp = S­_xq + S_đáy = 2 400 + 600 = 3 000 (cm²) = 0,33 m².

Vậy cần 0,33 mét vuông giấy vừa đủ để dán tất cả các mặt của chiếc lồng đèn.

Bài 3 trang 53 SGK Toán 8 Chân trời sáng tạo tập 1

a) Tính diện tích xung quanh của hình chóp tam giác đều có độ dài cạnh đáy là \(10\)cm, chiều cao của mặt bên xuất phát từ đỉnh của hình chóp tam giác đều là \(12\)cm.

b) Tính diện tích toàn phần và thể tích của hình chóp tứ giác đều có độ dài cạnh đáy là \(72\)dm, chiều cao là \(68,1\)dm, chiều cao của mặt bên xuất phát từ đỉnh của hình chóp tứ giác đều là \(77\)dm.

Lời giải: 

a) Diện tích xung quanh của hình chóp tam giác đều là: \(\frac{{10.3}}{2}.12 = 180\) (\(c{m^2}\))

b) Diện tích xung quanh của hình chóp tứ giác đều là: \(\frac{{72.4}}{2}.77 = 11088\) (\(d{m^2}\))

Diện tích đáy của hình chóp tứ giác đều là: \({72^2}=5184\) (\(d{m^2}\))

Diện tích toàn phần của hình chóp tứ giác đều là: \(11088 + 5184 = 16 272\) (\(d{m^2}\))

Thể tích của hình chóp tứ giác đều là: \(\frac{1}{3}.5184.68,1=117676,8\) (\(d{m^3}\))

Bài 4 trang 53 SGK Toán 8 Chân trời sáng tạo tập 1

Bảo tàng Louvre (Pháp) có một kim tự tháp hình chóp tứ giác đều bằng kính (gọi là kim tự tháp Louvre) có chiều cao \(21,3\)m và cạnh đáy \(34\)m. Tính thể tích của kim tự tháp này.

Lời giải:

Thể tích của kim tự tháp Louvre là:

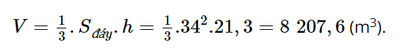
Vậy thể tích của kim tự tháp Louvre là 8 207,6 m³.

Giaibaitap.me