Bài 1 trang 61 SGK Toán 8 Chân trời sáng tạo tập 1

Cho tam giác \(ABC\) vuông tại \(A\).

a) Tính độ dài cạnh \(BC\) nếu biết \(AB = 7\)cm, \(AC = 24\)cm.

b) Tính độ dài cạnh \(AB\) biết \(AC = 2\)cm, \(BC = \sqrt {13} \)cm.

c) Tính độ dài cạnh \(AC\) nếu biết \(BC = 25\)cm, \(AB = 15\)cm.

Lời giải:

Áp dụng định lý Pythagore vào tam giác vuông \(ABC\) ta có:

a) \(B{C^2} = A{B^2} + A{C^2}\)

\(B{C^2} = {7^2} + {24^2} = 625 = {25^2}\)

\(BC = 25\) (cm)                                          

\(A{B^2} + {2^2} = {\sqrt {13} ^2}\)

b) \(A{B^2} + A{C^2} = B{C^2}\)

\(A{B^2} = {\sqrt {13} ^2} - {2^2} = 13 - 4 = 9 = {3^2}\)

\(AB = 3\) (cm)

c) \(A{B^2} + A{C^2} = B{C^2}\)

\({15^2} + A{C^2} = {25^2}\)

\(A{C^2} = {25^2} - {15^2} = 400 = {20^2}\)

\(AC = 20\) (cm)

Bài 2 trang 62 SGK Toán 8 Chân trời sáng tạo tập 1

Tính độ cao của con diều so với mặt đất (Hình 11)

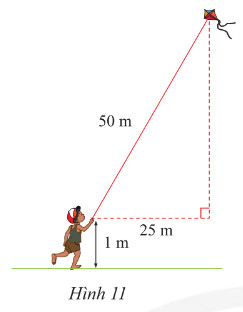
Lời giải:

Gọi \(x\) là độ cao của con diều so với mắt nhìn của người (m)

Áp dụng định lý Pythagore vào tam giác vuông trên hình ta có:

\({x^2} + {25^2} = {50^2}\)

\({x^2} = {50^2} - {25^2} = 1875\)

\(x = \sqrt {1875}  \approx 43,3\) (m)

Chiều cao của con diều so với mặt đất là:

\(43,3 + 1 = 44,3\) (m)

Bài 3 trang 62 SGK Toán 8 Chân trời sáng tạo tập 1

Lần lượt tính độ dài các cạnh huyền \(a\), \(b\), \(c\), \(d\) của các tam giác vuông trong Hình 12. Hãy dự đoán kết quả của các cạnh huyền còn lại.

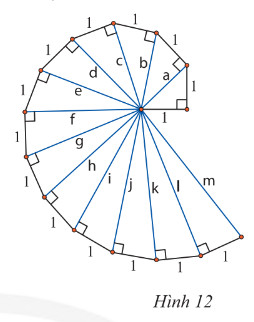
Lời giải: 

Bài 4 trang 62 SGK Toán 8 Chân trời sáng tạo tập 1

Chứng minh rằng tam giác \(ABC\) vuông trong các trường hợp sau:

a) \(AB = 8\)cm, \(AC = 15\)cm, \(BC = 17\)cm

b) \(AB = 29\)cm, \(AC = 21\)cm, \(BC = 20\)cm

c) \(AB = 12\)cm, \(AC = 37\), \(BC = 35\)cm

Lời giải: 

a) Ta có: 17² = 8² + 15². Suy ra BC² = AB² + AC².

Vậy tam giác ABC vuông tại A.

b) Ta có 29² = 20² + 21². Suy ra AB² = BC² + AC².

Vậy tam giác ABC vuông tại C.

c) Ta có 37² = 12² + 35². Suy ra AC² = AB² + BC².

Vậy tam giác ABC vuông tại B.

Bài 5 trang 62 SGK Toán 8 Chân trời sáng tạo tập 1

Cho biết thang của một xe máy cứu hỏa có chiều dài \(13\)m, chân thang cách mặt đất \(3\)m và cách tường của toàn nhà \(5\)m. Tính chiều cao mà thang có thể vươn tới.

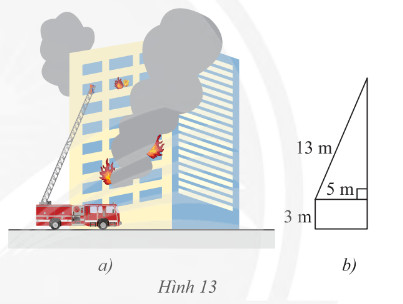
Lời giải:

Gọi \(x\) là khoảng cách của xe đến đầu thang (m)

Áp dụng định lý Pythagore vào tam giác vuông trong hình ta có:

\({x^2} + {5^2} = {13^2}\)

\({x^2} = {13^2} - {5^2} = 144 = {12^2}\)

\(x = 12\) (m)

Chiều cao mà thang có thể vươn tới là:

\(12 + 3 = 15\) (m)

Bài 6 trang 62 SGK Toán 8 Chân trời sáng tạo tập 1

Một con thuyền đang neo ở một điểm cách chân tháp hải đăng \(180\)m. Cho biết tháp hải đăng cao \(25\)m. Hãy tính khoảng cách từ thuyền đến đỉnh tháp hải đăng.

Lời giải:

Đặt các điểm A, B lần lượt là vị trí của đỉnh tháp hải đăng, chân tháp hải đăng và C là vị trí của con thuyền.

Áp dụng định lí Pythagore cho tam giác ABC vuông tại B, ta có:

AC² = AB² + BC² = 25² + 180² = 625 + 32 400 = 33 025.

Suy ra AC ≈ 181,73 (m).

Vậy khoảng cách từ thuyền đến ngọn hải đăng khoảng 181,73 m.

Giaibaitap.me