Bài 1 trang 65 SGK Toán 8 Chân trời sáng tạo tập 2

Trong hai khẳng định sau, khẳng định nào đúng, khẳng định nào sai? Tại sao?

a) Hai tam giác bằng nhau thì đồng dạng với nhau.

b) Hai tam giác đồng với với nhau thì bằng nhau.

Lời giải:

a) Xét khẳng định a: Hai tam giác bằng nhau thì đồng dạng với nhau.

Hai tam giác bằng nhau có các cặp góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau nên chúng đồng dạng theo tỉ số 1.

Vậy khẳng định a đúng.

b) Xét khẳng định b: Hai tam giác đồng dạng với nhau thì bằng nhau.

Hai tam giác đồng dạng có các cặp góc tương ứng bằng nhau và các cặp cạnh tương ứng tỷ lệ với nhau theo tỉ số k.

• Với k = 1 thì các cạnh tương ứng của hai tam giác đó bằng nhau nên hai tam giác đó bằng nhau.

• Với k ≠ 1 thì các cạnh tương ứng của hai tam giác đó không bằng nhau nên hai tam giác đó không bằng nhau.

Vậy khẳng định b sai.

Bài 2 trang 65 SGK Toán 8 Chân trời sáng tạo tập 2

Cho tam giác \(ABC\), hãy vẽ một tam giác đồng dạng với tam giác \(ABC\) theo tỉ số đồng dạng \(k = \frac{1}{2}\).

Lời giải:

Bước 1: Vẽ tam giác \(ABC\) bất kì.

Bước 2: Gọi \(M\) là trung điểm của \(AB\), \(N\) là trung điểm của \(AC\).

Khi đó ta có \(\Delta AMN\backsim\Delta ABC\) theo tỉ số \(k = \frac{1}{2}\).

Chứng minh:

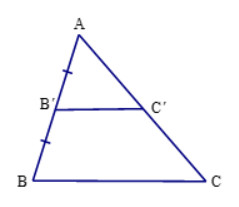
Vì \(M\) là trung điểm của \(AB\), \(N\) là trung điểm của \(AC\) nên \(MN\) là đường trung bình của tam giác \(ABC\)\( \Rightarrow \left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right.\).

Ta có \(MN//BC\) và \(M,N\) cắt \(AB,AC\) tại \(M,N\) nên \(\Delta AMN\backsim\Delta ABC\) (định lí).

Khi đó, \(\frac{{MN}}{{BC}} = \frac{1}{2}\).

Bài 3 trang 65 SGK Toán 8 Chân trời sáng tạo tập 2

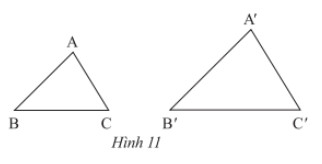
a) Trong Hình 11, cho biết \(\Delta ABC\backsim\Delta A'B'C'\). Viết tỉ số của các cạnh tương ứng và chỉ ra các cặp góc tương ứng.

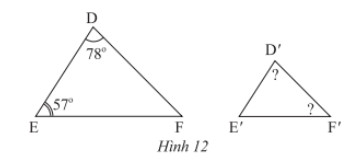
b) Trong Hình 12, cho biết \(\Delta DEF\backsim\Delta D'E'F'\). Tính số đo \(\widehat {D'}\) và \(\widehat F\).

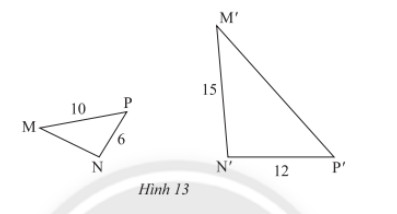
c) Trong Hình 12, cho biết \(\Delta MNP\backsim\Delta M'N'P'\). Tính độ dài các đoạn thẳng \(MN\) và \(MP'\).

Lời giải:

Bài 4 trang 66 SGK Toán 8 Chân trời sáng tạo tập 2

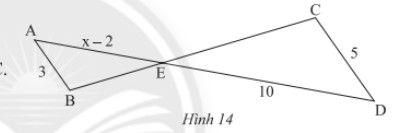
Trong Hình 14, cho biết \(AB//CD\)

a) Chứng minh rằng \(\Delta AEB\backsim\Delta DEC\).

b) Tìm \(x\).

Lời giải:

a) Xét tam giác \(ABE\) có:

\(AB//CD\) và \(C,D\) cắt \(BE;AE\) lần lượt tại \(C,D\).

Do đó, \(\Delta AEB\backsim\Delta DEC\) (định lí)

b) Vì \(\Delta AEB\backsim\Delta DEC\) nên \(\frac{{AE}}{{ED}} = \frac{{AB}}{{CD}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).

Thay số ta được:

\(\frac{{x - 2}}{{10}} = \frac{3}{5} \Rightarrow x - 2 = \frac{{10.3}}{5} = 6 \Rightarrow x = 6 + 2 = 8\)

Vậy \(x = 8\).

Bài 5 trang 66 SGK Toán 8 Chân trời sáng tạo tập 2

Cho \(\Delta ABC\backsim\Delta DEF\) theo tỉ sống đồng dạng \(k = \frac{2}{5}\).

a) Tính tỉ số chu vi của hai tam giác đã cho.

b) Cho biết hiệu chu vi hai tam giác trên là 36cm, tính chu vi mỗi tam giác.

Lời giải:

Bài 6 trang 66 SGK Toán 8 Chân trời sáng tạo tập 2

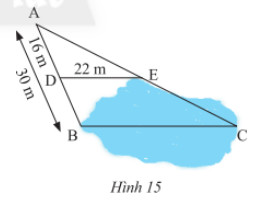
Người ta ứng dụng hai tam giác đồng dạng để đo khoảng cách \(BC\) ở hai điểm không thể đến được (hình 15). Biết \(DE//BC\).

a) Chứng minh rằng \(\Delta ADE\backsim\Delta ABC\).

b) Tính khoảng cách \(BC\).

Lời giải:

a) Xét tam giác \(ABC\) ta có:

\(DE//BC\) và \(D,E\) cắt \(AB;AC\) tại \(D;E\).

Do đó, \(\Delta ADE\backsim\Delta ABC\) (định lí)

b) Vì \(\Delta ADE\backsim\Delta ABC\) nên \(\frac{{AD}}{{AB}} = \frac{{DE}}{{BC}}\) (cách cặp cạnh tương ứng có cùng tỉ lệ).

Thay số, \(\frac{{16}}{{30}} = \frac{{22}}{{BC}} \Rightarrow BC = \frac{{22.30}}{{16}} = 41,25\)

Vậy \(BC = 41,25m\).

Giaibaitap.me