Bài 1 trang 66 SGK Toán 8 Chân trời sáng tạo tập 1

Tìm số đo các góc chưa biết của các tứ giác trong Hình 11.

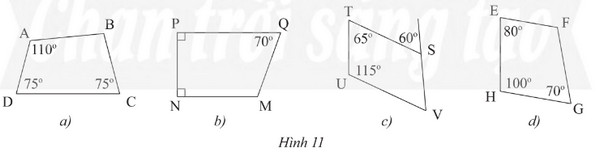
Lời giải:

a) Trong tứ giác \(ABCD\) có: 

\(\begin{array}{l}\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \\110^\circ  + \widehat B + 75^\circ  + 75^\circ  = 360^\circ \\\widehat B = 360^\circ  - \left( {110^\circ  + 75^\circ  + 75^\circ } \right)\\\widehat B = 100^\circ \end{array}\)

b) Trong tứ giác \(MNPQ\) ta có:

\(\begin{array}{l}\widehat P + \widehat Q + \widehat M + \widehat N = 360^\circ \\90^\circ  + 70^\circ  + \widehat M + 90^\circ  = 360^\circ \\\widehat M = 360^\circ  - \left( {90^\circ  + 70^\circ  + 90^\circ } \right)\\\widehat M = 110^\circ \end{array}\)

c) Ta có: \(\widehat {TSV} = 180^\circ  - 60^\circ  = 120^\circ \)

Xét tứ giác \(UTSV\) ta có:

\(\begin{array}{l}\widehat U + \widehat T + \widehat S + \widehat V = 360^\circ \\115^\circ  + 65^\circ  + 120^\circ  + \widehat V = 360^\circ \\\widehat V = 360^\circ  - \left( {115^\circ  + 65^\circ  + 120^\circ } \right)\\\widehat V = 60^\circ \end{array}\)

d) Trong tứ giác \(EFGH\) có:

\(\begin{array}{l}\widehat F + \widehat E + \widehat G + \widehat H = 360^\circ \\\widehat F + 80^\circ  + 100^\circ  + 70^\circ  = 360^\circ \\\widehat F = 360^\circ  - \left( {80^\circ  + 100^\circ  + 70^\circ } \right)\\\widehat F = 110^\circ \end{array}\)

Bài 2 trang 66 SGK Toán 8 Chân trời sáng tạo tập 1

Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác đó.

Hãy tính tổng số đo bốn góc ngoài \(\widehat {{A_1}};\;\widehat {{B_1}};\;\widehat {{C_1}};\;\widehat {{D_1}}\) của tứ giác \(ABCD\) ở hình 12.

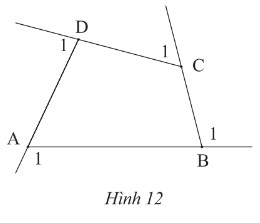
Lời giải:

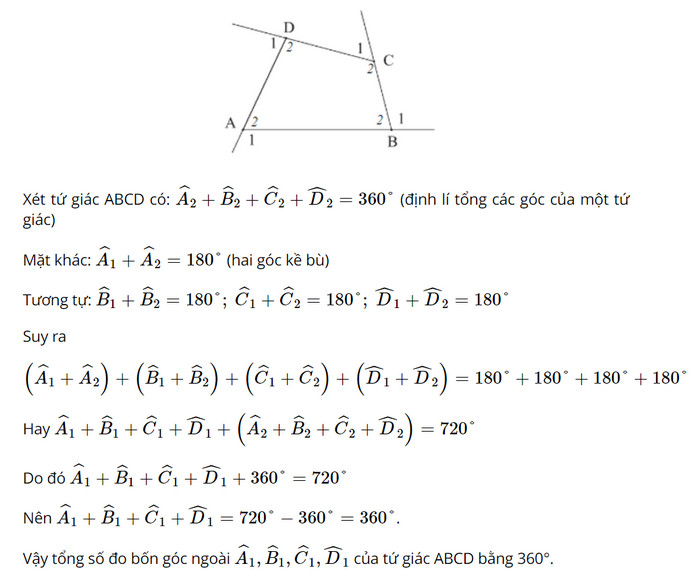
Bài 3 trang 67 SGK Toán 8 Chân trời sáng tạo tập 1

Tứ giác \(ABCD\) có \(\widehat A = 100^\circ \), góc ngoài tại đỉnh \(B\) bằng \(110^\circ \), \(\widehat C = 75^\circ \). Tính số đo góc \(D\)

Lời giải: 

Ta có: \(\widehat B = 180^\circ  - 110^\circ  = 70^\circ \) (vì tổng góc trong và góc ngoài tại một đỉnh bằng \(180^0\))

Trong tứ giác \(ABCD\) có tổng bốn góc bằng \(360^\circ \) nên:

\(\widehat D = 360^\circ  - \left( {100^\circ  + 70^\circ  + 75^\circ } \right) = 115^\circ \)

Bài 4 trang 67 SGK Toán 8 Chân trời sáng tạo tập 1

Tứ giác \(ABCD\) có góc ngoài tại đỉnh \(A\) bằng \(65^\circ \), góc ngoài tại đỉnh \(B\) bằng \(100^\circ \), góc ngoài tại đỉnh \(C\) bằng \(60^\circ \). Tính số đo góc ngoài tại đỉnh \(D\).

Lời giải: 

Bài 5 trang 67 SGK Toán 8 Chân trời sáng tạo tập 1

Tứ giác \(ABCD\) có số đo \(\widehat A = x;\;\widehat B = 2x;\;\widehat C = 3x;\;\widehat D = 4x\). Tính số đo các góc của tứ giác đó.

Lời giải:

Trong tứ giác \(ABCD\), tổng các góc bằng \(360^\circ \) nên ta có:

\(\begin{array}{l}x + 2x + 3x + 4x = 360^\circ \\10x = 360^\circ \\x = 360^\circ :10\\x = 36^\circ \end{array}\)

Suy ra:

\(\widehat A = 36^\circ ;\;\widehat B = 72^\circ ;\;\widehat C = 108^\circ ;\;\widehat D = 144^\circ \)

Bài 6 trang 67 SGK Toán 8 Chân trời sáng tạo tập 1

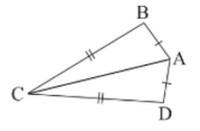
Ta gọi tứ giác ABCD với AB = AD, CB = CD (hình 13) là hình “cái diều”.

a. Chứng minh rằng AC là đường trung trực của BD.

b. Cho biết \(\widehat B = {95^0},\widehat C = {35^0}.\)Tính \(\widehat A\) và \(\widehat D\)

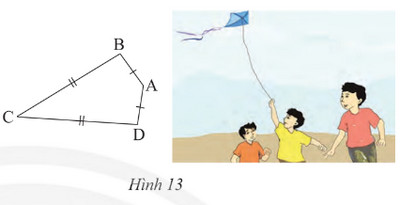
Lời giải:

a) Vì AB = AD nên A nằm trên đường trung trực của đoạn thẳng BD.

Vì CB = CD nên C nằm trên đường trung trực của đoạn thẳng BD.

Do đó AC là đường trung trực của đoạn thẳng BD.

b) Xét DABC và DADC có:

AC là cạnh chung; AB = AD; BC = DC (giả thiết).

Do đó DABC = DADC (c.c.c).

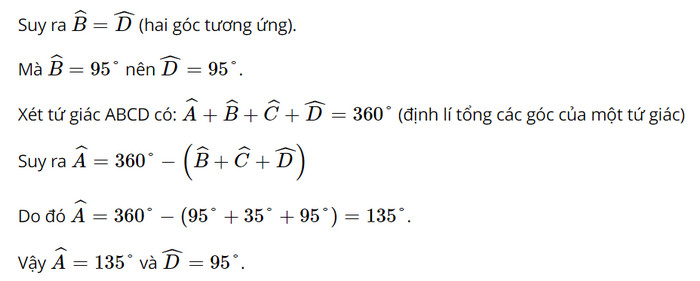
Bài 7 trang 67 SGK Toán 8 Chân trời sáng tạo tập 1

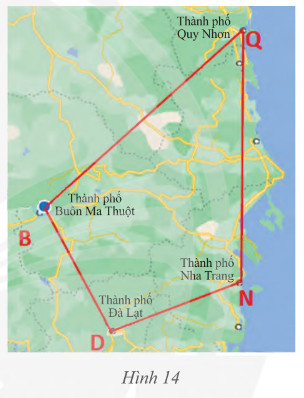
Trên bản đồ, tứ giác \(BDNQ\) với các đỉnh là các thành phố Buôn Ma Thuột, Đà Lạt, Nha Trang, Quy Nhơn.

a) Tìm các cạnh kề và cạnh đối diện của cạnh \(BD\).

b) Tìm các đường chéo của tứ giác

Lời giải:

a) Các cạnh kề của \(BD\) là: \(BQ\), \(DN\)

Cạnh đối của cạnh \(BD\) là: \(NQ\)

b) Các đường chéo của tứ giác là: \(BN;\;DQ\)

Giaibaitap.me