A. TRẮC NGHIỆM
Bài 1 trang 84 SGK Toán 8 Chân trời sáng tạo tập 2
Trong các khẳng định sau, khẳng định nào đúng?
A. Hai tam giác đồng dạng thì bằng nhau.
B. Hai tam giác bằng nhau thì đồng dạng.
C. Hai tam giác bằng nhau thì không đồng dạng.
D. Hai tam giác cân thì luôn đồng dạng
Lời giải:
Đáp án đúng là: B
Hai tam giác bằng nhau thì đồng dạng với theo tỉ số k = 1.
Bài 2 trang 84 SGK Toán 8 Chân trời sáng tạo tập 2
Nếu \(\Delta ABC\backsim\Delta MNP\) theo tỉ số \(k = 3\) thì \(\Delta MNP\backsim\Delta ABC\) theo tỉ số
A. \(\frac{1}{3}\).
B. \(\frac{1}{9}\).
C. \(3\).
D. \(9\).
Lời giải:
Đáp án đúng là A
Vì \(\Delta ABC\backsim\Delta MNP\) theo tỉ số \(k = 3\) nên \(\Delta MNP\backsim\Delta ABC\) theo tỉ số \(\frac{1}{3}\).
Bài 3 trang 84 SGK Toán 8 Chân trời sáng tạo tập 2
Nếu \(\Delta ABC\)có \(MN//AB\) (với \(M \in AC,N \in BC\)) thì
A. \(\Delta CMN\backsim\Delta ABC\).
B. \(\Delta CNM\backsim\Delta CAB\).
C. \(\Delta CNM\backsim\Delta ABC\).
D. \(\Delta MNC\backsim\Delta ABC\).
Lời giải:
Đáp án đúng là: D
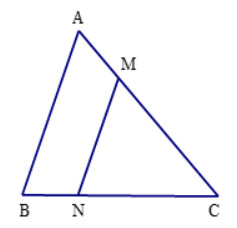
Xét tam giác ABC có MN // AB nên ΔMNC ᔕ ΔABC.
Bài 4 trang 84 SGK Toán 8 Chân trời sáng tạo tập 2
Cho \(\Delta ABD\backsim\Delta DEF\)với tỉ số đồng dạng \(k = \frac{1}{3}\), biết \(AB = 9cm\). Khi đó, \(DE\) bằng
A. 6 cm.
B. 12 cm.
C. 3 cm.
D. 27 cm.
Lời giải:
Đáp án đúng là D
Vì \(\Delta ABD\backsim\Delta DEF\) với tỉ số đồng dạng là \(k = \frac{1}{3}\) nên \(\frac{{AB}}{{DE}} = \frac{{AD}}{{DF}} = \frac{{BD}}{{EF}} = \frac{1}{3}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Do đó, \(\frac{{AB}}{{DE}} = \frac{1}{3} \Rightarrow \frac{9}{{DE}} = \frac{1}{3} \Rightarrow DE = \frac{{9.3}}{1} = 27\)
Vậy \(DE = 27cm.\)
Bài 5 trang 84 SGK Toán 8 Chân trời sáng tạo tập 2
Nếu tam giác \(ABC\) và tam giác \(EFG\) có \(\widehat A = \widehat E;\widehat B = \widehat F\) thì
A. \(\Delta ABC\backsim\Delta EGF\).
B. \(\Delta ABC\backsim\Delta EFG\).
C. \(\Delta ACB\backsim\Delta GFE\).
D. \(\Delta CBA\backsim\Delta FGE\).
Lời giải:
Đáp án đúng là: B
Xét ΔABC và ΔEFG có:
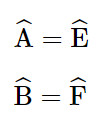
Do đó ΔABC ᔕ ΔEFG (g.g).
Bài 6 trang 84 SGK Toán 8 Chân trời sáng tạo tập 2
Cho \(\Delta XYZ\backsim\Delta EFG\), biết \(XY = 6cm;EF = 8cm;EG = 12cm\). Khi đó \(XZ\) bằng
A. 10 cm.
B. 9 cm.
C. 12 cm.
D. 16 cm.
Lời giải:
Đáp án đúng là B
Vì \(\Delta XYZ\backsim\Delta EFG\) nên \(\frac{{XY}}{{EF}} = \frac{{XZ}}{{EG}}\)(các cặp cạnh tương ứng có cùng tỉ lệ).
Thay số, \(\frac{6}{8} = \frac{{XZ}}{{12}} \Rightarrow XZ = \frac{{6.12}}{8} = 9\).
Vậy \(XZ = 9cm\).
Bài 7 trang 84 SGK Toán 8 Chân trời sáng tạo tập 2
Cho \(\Delta ABC\backsim\Delta DEF\), biết \(\widehat A = 85^\circ ,\widehat B = 60^\circ \). Khi đó số đo \(\widehat F\) bằng
A.\(60^\circ \).
B. \(85^\circ \).
C. \(35^\circ \).
D. \(45^\circ \).
Lời giải:
Đáp án đúng là: C
Ta có: ΔABC ᔕ ΔDEF nên
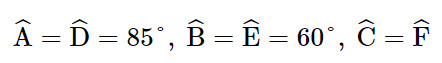
Do đó 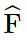 =180°−(85°+60°)=35°
=180°−(85°+60°)=35°
Bài 8 trang 84 SGK Toán 8 Chân trời sáng tạo tập 2
Cho hình thang \(ABCD\left( {AB//CD} \right)\), có hai đường chéo \(AC\) và \(DB\) cắt nhau tại \(O\). Biết \(AB = 8cm,CD = 20cm\). Khi đó \(\Delta AOB\backsim\Delta COD\) với tỉ số đồng dạng là
A.\(k = \frac{2}{3}\).
B. \(k = \frac{3}{2}\).
C. \(k = \frac{2}{5}\).
D. \(k = \frac{5}{2}\).
Lời giải:
Đáp án đúng là C
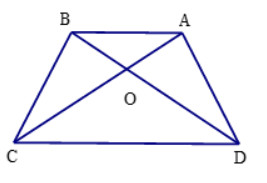
Vì \(ABCD\) và \(AB//CD\) nên \(\widehat {OAB} = \widehat {OCD}\) (hai góc ở vị trí so le trong)
Xét tam giác \(AOB\) và tam giác \(COD\) có:
\(\widehat {OAB} = \widehat {OCD}\) (chứng minh trên)
\(\widehat {AOB} = \widehat {COD}\) (hai góc đối đỉnh)
Suy ra, \(\Delta AOB\backsim\Delta COD\) (g.g)
Suy ra, tỉ số đồng dạng \(k = \frac{{AB}}{{CD}} = \frac{8}{{20}} = \frac{2}{5}\).
B. TỰ LUẬN
Bài 9 trang 85 SGK Toán 8 Chân trời sáng tạo tập 2
Trong Hình 1, cho biết \(\widehat {ABD} = \widehat {ACB},AC = 9cm,AD = 4cm\).
a) Chứng minh tam giác \(\Delta ABD\backsim\Delta ACB\).
b) Tính độ dài cạnh \(AB\).
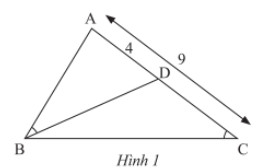
Lời giải:
a) Xét ∆ABD và ∆ACB có:
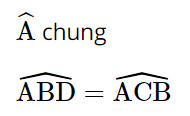
Do đó ΔABD ᔕ ΔACB (g.g).
b) Từ câu a: ΔABD ᔕ ΔACB nên 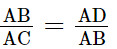
Khi đó AB2 = AC.AD = 9.4 = 36
Do đó AB = 6 cm.
Bài 10 trang 85 SGK Toán 8 Chân trời sáng tạo tập 2
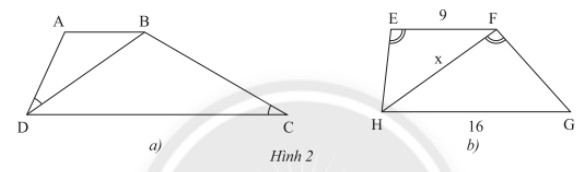
a) Cho hình thang \(ABCD\left( {AB//CD} \right)\), biết \(\widehat {ADB} = \widehat {DCB}\) (Hình 2a).
Chứng minh rằng \(B{D^2} = AB.CD\).
b) Cho hình thang \(EFGH\left( {FF//GH} \right),\widehat {HEF} = \widehat {HFG},EF = 9m,GH = 16m\) (Hình 2b).
Tính độ dài \(x\) của \(HF\).
Lời giải:
a) Vì \(ABCD\) là hình thang có \(AB//CD\) nên \(\widehat {ABD} = \widehat {BDC}\) (hai góc so le trong)
Xét tam giác \(ABD\) và tam giác \(BDC\) có:
\(\widehat {ADB} = \widehat {DCB}\) (giả thuyết)
\(\widehat {ABD} = \widehat {BDC}\) (chứng minh trên)
Suy ra, \(\Delta ABD\backsim\Delta BDC\) (g.g)
Suy ra, \(\frac{{AB}}{{BD}} = \frac{{BD}}{{CD}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra, \(B{D^2} = AB.CD\).
b) Vì \(EFGH\) là hình thang có \(FF//GH\)nên \(\widehat {EFH} = \widehat {FHG}\) (hai góc so le trong)
Xét tam giác \(EFH\) và tam giác \(FHG\) có:
\(\widehat {HEF} = \widehat {HFG}\) (giả thuyết)
\(\widehat {EFH} = \widehat {FHG}\) (chứng minh trên)
Suy ra, \(\Delta EFH\backsim\Delta FHG\) (g.g)
Suy ra, \(\frac{{EF}}{{FH}} = \frac{{FH}}{{HG}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra, \(F{H^2} = EF.HG = 9.16 = 144 \Rightarrow FH = \sqrt {144} = 12\).
Vậy \(FH = 12cm\).
Bài 11 trang 85 SGK Toán 8 Chân trời sáng tạo tập 2
a) Tính khoảng cách \(HM\) của mặt hồ ở Hình 3a.
b) Tính khoảng cách \(MN\) của một khúc sông ở Hình 3b.

Lời giải:
a) Xét hai tam giác vuông HEF và HMN ta có: 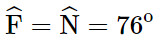
Do đó ΔHEF ᔕ ΔHMN (g.g)
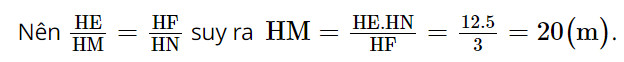
Vậy khoảng cách HM của mặt hồ ở Hình 3a là 20 m.
b) Xét hai tam giác vuông IMN và IEF có:
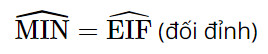
Do đó ΔIMN ∽ ΔIEF (g.g)
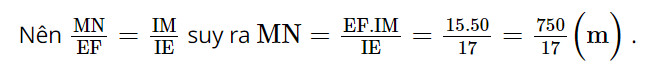
Vậy khoảng cách MN của một khúc sông ở Hình 3b là 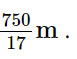
Bài 12 trang 85 SGK Toán 8 Chân trời sáng tạo tập 2
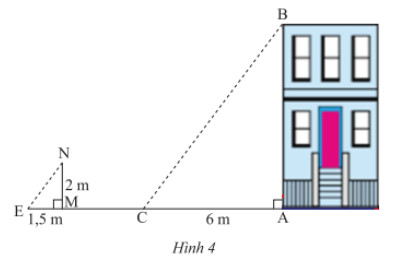
Bóng của một căn nhà trên mặt đất có độ dài 6 m. Cùng thời điểm đó, một cọc sắt cao 2 m cắm vuông góc với mặt đất có bóng dài 1,5m (Hình 4). Tính chiều cao của ngôi nhà.
Lời giải:
Vì cùng một thời điểm thì góc tạo bởi tia nắng mặt trời và mặt đất là những góc bằng nhau. Do đó, \(\widehat {NEM} = \widehat {BCA}\).
Xét tam giác \(NEM\) và tam giác \(BCA\) có:
\(\widehat {NEM} = \widehat {BCA}\) (chứng minh trên)
\(\widehat {NME} = \widehat {BAC} = 90^\circ \) (giải thuyết)
Suy ra, \(\Delta NEM\backsim\Delta BCA\) (g.g)
Suy ra, \(\frac{{EM}}{{CA}} = \frac{{MN}}{{AB}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{1,5}}{6} = \frac{2}{{AB}} \Rightarrow AB = \frac{{2.6}}{{1,5}} = 8\).
Vậy chiều cao của ngôi nhà là 8m.
Bài 13 trang 86 SGK Toán 8 Chân trời sáng tạo tập 2
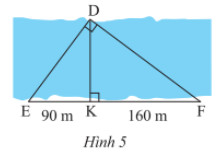
Người ta đo khoảng cách giữa hai điểm \(D\) và \(K\) ở hai bờ một dòng song (Hình 5). Cho biết \(KE = 90m,KF = 160m\). Tính khoảng cách \(DK\).
Lời giải:
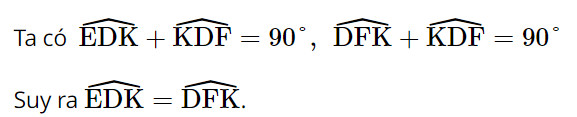
Xét hai tam giác vuông DKE và FKD có:
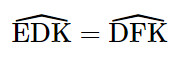
Suy ra ΔDKE ∽ ΔFKD (g.g)
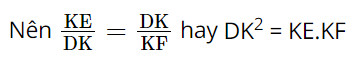
Do đó DK2 = 90.160 =14 400 suy ra DK = 120 m.
Vậy khoảng cách DK bằng 120 m.
Bài 14 trang 86 SGK Toán 8 Chân trời sáng tạo tập 2
Cho tam giác \(ABC\)nhọn có hai đường cao \(BE,CF\) cắt nhau tại \(H\). Chứng minh rằng
a) \(\Delta AEB\backsim\Delta AFC\).
b) \(\frac{{HE}}{{HC}} = \frac{{HF}}{{HB}}\).
c) \(\Delta HEF\backsim\Delta HCB\)
Lời giải:
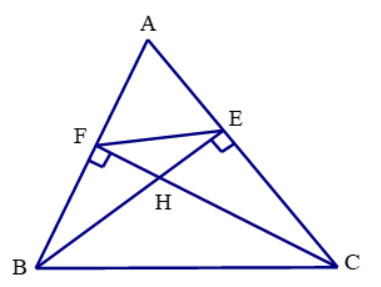
a) Vì \(BE\)là đường cao nên \(\widehat {AEB} = 90^\circ \); vì \(CF\)là đường cao nên \(\widehat {AFC} = 90^\circ \)
Xét tam giác \(AEB\) và tam giác \(AFC\) có:
\(\widehat A\) (chung)
\(\widehat {AEB} = \widehat {AFC} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta AEB\backsim\Delta AFC\) (g.g).
b) Vì \(\Delta AEB\backsim\Delta AFC\) nên \(\widehat {ACF} = \widehat {ABE}\) (hai góc tương ứng) hay \(\widehat {ECH} = \widehat {FBH}\).
Xét tam giác \(HEC\) và tam giác \(HFB\) có:
\(\widehat {ECH} = \widehat {FBH}\) (chứng minh trên)
\(\widehat {CEH} = \widehat {BFH} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta HEC\backsim\Delta HFC\) (g.g).
Suy ra, \(\frac{{HE}}{{HF}} = \frac{{HC}}{{HB}}\) (các cặp cạnh tương ứng tỉ lệ)
Hay \(\frac{{HE}}{{HC}} = \frac{{HF}}{{HB}}\) (điều phải chứng minh).
c) Xét tam giác \(HEF\) và tam giác \(HCB\) có:
\(\widehat {FHE} = \widehat {BHC}\) (hai góc đối đỉnh)
\(\frac{{HE}}{{HC}} = \frac{{HF}}{{HB}}\) (chứng minh trên)
Suy ra, \(\Delta HEF\backsim\Delta HCB\) (c.g.c).
Bài 15 trang 86 SGK Toán 8 Chân trời sáng tạo tập 2
Cho tam giác \(ABC\) nhọn có hai đường cao \(BM,CN\) cắt nhau tại \(H\).
a) Chứng minh rằng \(\Delta AMN\backsim\Delta ABC\).
b) Phân giác của \(\widehat {BAC}\) cắt \(MN\) và \(BC\) lần lượt tại \(I\) và \(K\). Chứng minh rằng \(\frac{{IM}}{{IN}} = \frac{{KB}}{{KC}}\).
Lời giải:
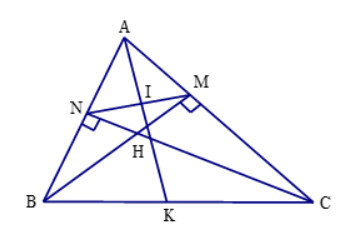
a) Xét tam giác vuông ABM và ACN có:

Suy ra ΔABM ᔕ ΔACN (g.g)
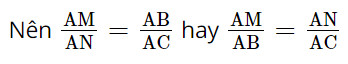
Xét tam giác AMN và ABC ta có:
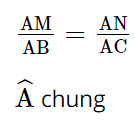
Suy ra ΔAMN ∽ ΔABC (c.g.c).

Bài 16 trang 86 SGK Toán 8 Chân trời sáng tạo tập 2
Cho tam giác \(ABC\) vuông tại \(A\left( {AB < AC} \right)\). Kẻ đường cao \(AH\left( {H \in BC} \right)\).
a) Chứng minh rằng \(\Delta ABH\backsim\Delta CBA\), suy ra \(A{B^2} = BH.BC\).
b) Vẽ \(HE\) vuông góc với \(AB\) tại \(E\), vẽ \(HF\) vuông góc với \(AC\) tại \(F\). Chứng minh rằng \(AE.AB = AF.AC\).
c) Chứng minh rằng \(\Delta AFE\backsim\Delta ABC\).
d) Qua \(A\) vẽ đường thẳng song song với \(BC\) cắt đường thẳng \(HF\) tại \(I\). Vẽ \(IN\) vuông góc với \(BC\) tại \(N\). Chứng minh rằng \(\Delta HNF\backsim\Delta HIC\).
Lời giải:
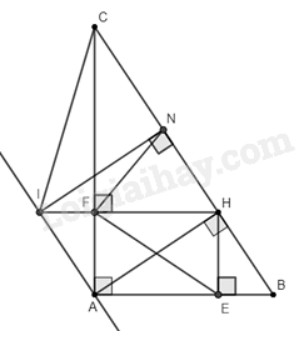
a) Vì \(AH\) là đường cao nên \(\widehat {AHB} = \widehat {AHC} = 90^\circ \)
Xét tam giác \(ABH\) và tam giác \(CBA\) có:
\(\widehat B\) (chung)
\(\widehat {AHB} = \widehat {CAB} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta ABH\backsim\Delta CBA\) (g.g).
Do đó, \(\frac{{AB}}{{CB}} = \frac{{BH}}{{AB}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra, \(A{B^2} = BH.BC\) .
b)
- Vì \(HE\) vuông góc với \(AB\) nên \(\widehat {HEA} = \widehat {HEB} = 90^\circ \)
Xét tam giác \(AHE\) và tam giác \(ABH\) có:
\(\widehat {HAE}\) (chung)
\(\widehat {HEA} = \widehat {AHB} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta AHE\backsim\Delta ABH\) (g.g).
Do đó, \(\frac{{AH}}{{AB}} = \frac{{AE}}{{AH}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra, \(A{H^2} = AB.AE\) . (1)
- Vì \(HF\) vuông góc với \(AC\) nên \(\widehat {HFC} = \widehat {HFA} = 90^\circ \)
Xét tam giác \(AHF\) và tam giác \(ACH\) có:
\(\widehat {HAF}\) (chung)
\(\widehat {AFH} = \widehat {AHC} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta AHF\backsim\Delta ACH\) (g.g).
Do đó, \(\frac{{AH}}{{AC}} = \frac{{AF}}{{AH}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra, \(A{H^2} = AF.AC\) . (2)
Từ (1) và (2) suy ra, \(AE.AB = AF.AC\) (điều phải chứng minh)
c) Vì \(AE.AB = AF.AC \Rightarrow \frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}\).
Xét tam giác \(AFE\) và tam giác \(ABC\) có:
\(\widehat A\) (chung)
\(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}\) (chứng minh trên)
Suy ra, \(\Delta AFE\backsim\Delta ABC\) (c.g.c).
d) Vì \(HF\) vuông góc với \(AC\) nên \(CF \bot HI\), do đó, \(\widehat {CFH} = \widehat {CFI} = 90^\circ \).
Vì \(IN \bot CH \Rightarrow \widehat {CBI} = \widehat {HNI} = 90^\circ \).
Xét tam giác \(HFC\) và tam giác \(HNI\) có:
\(\widehat {CHI}\) (chung)
\(\widehat {HFC} = \widehat {HNI} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta HFC\backsim\Delta HNI\) (g.g).
Suy ra, \(\frac{{HF}}{{HN}} = \frac{{HC}}{{HI}}\) (hai cặp cạnh tương ứng cùng tỉ lệ)
Do đó, \(\frac{{HF}}{{HC}} = \frac{{HN}}{{HI}}\).
Xét tam giác \(HNF\) và tam giác \(HIC\) có:
\(\widehat {CHI}\) (chung)
\(\frac{{HF}}{{HC}} = \frac{{HN}}{{HI}}\) (chứng minh trên)
Suy ra, \(\Delta HNF\backsim\Delta HIC\) (c.g.c).
Bài 17 trang 86 SGK Toán 8 Chân trời sáng tạo tập 2
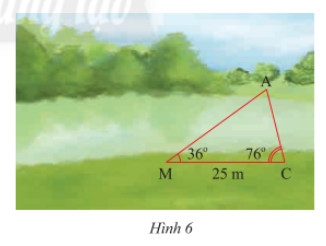
Quan sát Hình 6. Vẽ vào tờ giấy tam giác \(DEF\) với \(EF = 4cm,\widehat E = 36^\circ ,\widehat F = 76^\circ \).
a) Chứng minh \(\Delta DEF\backsim\Delta AMC\).
b) Dùng thước đo chiều dài cạnh \(DF\) của \(\Delta DEF\). Tính khoảng cách giữa hia điểm \(A\) và \(C\) ở hai bờ sông trong Hình 6.
Lời giải:
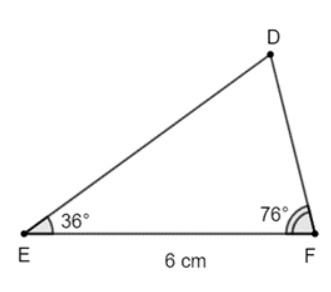
a) Xét tam giác \(DEF\) và tam giác \(AMC\) có:
\(\widehat E = \widehat M = 36^\circ \)
\(\widehat F = \widehat C = 76^\circ \) (chứng minh trên)
Suy ra, \(\Delta DEF\backsim\Delta AMC\) (g.g).
b) Đổi 25m = 2500 cm.
Dùng thước đo độ dài cạnh \(DF\) ta được độ dài \(DF\) là 2,6cm.
Vì \(\Delta DEF\backsim\Delta AMC\) nên \(\frac{{DF}}{{EF}} = \frac{{AC}}{{MC}}\) (hai cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{2,6}}{4} = \frac{{AC}}{{2500}} \Rightarrow AC = \frac{{2,6.2500}}{4} = 1625\).
Vậy khoảng cách giữa hai điểm \(A\) và \(C\) là 1625 cm hay 16,25m.
Giaibaitap.me
Giải bài tập SGK Toán 8 trang 90, 91 Chân trời sáng tạo tập 2 - Bài 1 Mô tả xác suất bằng tỉ số. Một hộp chứ 3 viên bi xanh, 4 viên bi đỏ và 5 viên bi vàng có kích thước và khối lượng giống nhau. Lấy ra ngẫu nhiên 1 viên bi từ hộp. Tính xác suất của các biến cố:
Giải bài tập SGK Toán 8 trang 94 Chân trời sáng tạo tập 2 - Bài 2 Xác suất lí thuyết và xác suất thực nghiệm. Ở một sân bay người ta nhận thấy với mỗi chuyến bay, xác suất tất cả mọi người đều có mặt để lên máy bay là 0,9. Trong một ngày, sân bay có 120 lượt máy bay cất cánh. Hãy ước lượng số chuyến bay trong ngày hôm đó có người mua vé nhưng không lên máy bay.
Giải bài tập SGK Toán 8 trang 95, 96 Chân trời sáng tạo tập 2 - Bài tập cuối chương 9. Một túi đựng 1 viên bi xanh, 1 viên bi đỏ, 1 viên bi trắng và 1 viên bi vàng có cùng kích thước và khối lượng. Lấy ngẫu nhiên 2 viên bi từ túi. Tính xác suất của các biến cố: