Bài 1 trang 70 SGK Toán 8 Chân trời sáng tạo tập 2

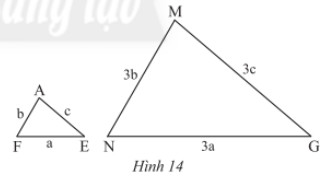
a) Tam giác \(AFE\) và \(MNG\) ở Hình 14 có đồng dạng với nhau không? Vì sao?

b) Biết tam giác \(AFE\) có chu vi bằng 15 cm. Tính chu vi tam giác MNG.

Lời giải:

a) Ta có:

\(\frac{{AF}}{{MN}} = \frac{b}{{3b}} = \frac{1}{3};\frac{{AE}}{{MG}} = \frac{c}{{3c}} = \frac{1}{3};\frac{{EF}}{{NG}} = \frac{a}{{3a}} = \frac{1}{3}\)

Xét tam giác \(AFE\) và tam giác \(MNG\) có:

\(\frac{{AF}}{{MN}} = \frac{1}{3};\frac{{AE}}{{MG}} = \frac{1}{3};\frac{{EF}}{{NG}} = \frac{1}{3} \Rightarrow \frac{{AF}}{{MN}} = \frac{{AE}}{{MG}} = \frac{{EF}}{{NG}}\)

Do đó, \(\Delta AFE\backsim\Delta MNG\) (c.c.c)

b) Tỉ số đồng dạng của tam giác \(AFE\) và tam giác \(MNG\)  là \(\frac{1}{3}\).

Do đó, tỉ số chu vi của của tam giác \(AFE\) và tam giác \(MNG\)  là \(\frac{1}{3}\) (tính chất)

Do đó, chu vi tam giác \(MNG\) là: \(15.3 = 45cm\)

Vậy chu vi tam giác \(MNG\) là 45 cm.

Bài 2 trang 70 SGK Toán 8 Chân trời sáng tạo tập 2

Tam giác \(ABC\) có độ dài \(AB = 4cm,AC = 6cm,BC = 9cm.\)Tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\) và có chu vi bằng 66,5 cm. Hãy tính độ dài các cạnh của tam giác \(A'B'C'\).

Lời giải:

Chu vi tam giác ABC: AB + AC + BC = 19.

Tỉ số chu vi của hai tam giác ABC và A'B'C' là: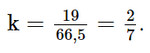 

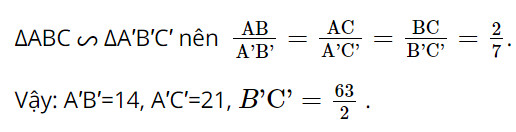
Bài 3 trang 70 SGK Toán 8 Chân trời sáng tạo tập 2

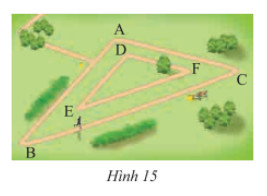
Một công viên có hai đường chạy bộ hình tam giác đồng dạng như Hình 15. Kích thước của con đường bên trong lần lượt là 300 m, 350 m và 550 m. Cạnh ngắn nhất của con đường bên ngoài là 600 m. Nam chạy bốn vòng bên trong. Hưng chạy hai vòng bên ngoài. So sánh quãng đường chạy của hai bạn.

Lời giải:

Quan sát hình vẽ ta thấy, cạnh ngắn nhất của tam giác \(ABC\) là cạnh \(AC\);cạnh ngắn nhất của tam giác \(DEF\) là cạnh \(DF\).

Do đó, ta có: \(\frac{{AC}}{{DF}} = \frac{{600}}{{300}} = 2\).

Do đó, tỉ số chu vi của tam giác \(ABC\) và tam giác \(DEF\) là 2.

Chu vi tam giác \(DEF\) là: \(300 + 350 + 550 = 1200m\)

Chu vi tam giác \(ABC\) là: \(1200.2 = 2400m\).

Quãng đường bạn Nam đã chạy là: \(1200.4 = 4800m\)

Quãng đường bạn Hùng đã chạy là: \(2400.2 = 4800m\).

Do đó, hai bạn Nam và Hùng đã chạy hai quãng đường bằng nhau.

Bài 4 trang 71 SGK Toán 8 Chân trời sáng tạo tập 2

Xét xem cặp tam giác nào trong Hình 16a,16b đồng dạng?

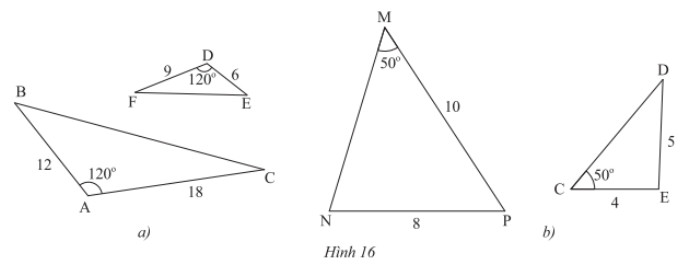
Lời giải:

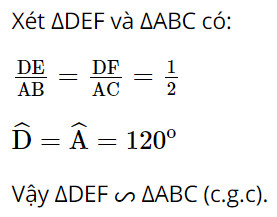
Bài 5 trang 71 SGK Toán 8 Chân trời sáng tạo tập 2

Trong Hình 17, cho biết \(DE = 6cm,EF = 7,8cm,NP = 13cm,NM = 10cm,\widehat E = \widehat N\) và \(\widehat P = 42^\circ \). Tính \(\widehat F\).

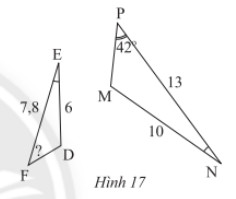
Lời giải:

Ta có:

\(\frac{{EF}}{{NP}} = \frac{{7,8}}{{13}} = \frac{3}{5};\frac{{DE}}{{MN}} = \frac{6}{{10}} = \frac{3}{5}\)

Xét tam giác \(DEF\) và tam giác \(MNP\) ta có:

\(\frac{{EF}}{{NP}} = \frac{{DE}}{{MN}} = \frac{3}{5}\)

\(\widehat E = \widehat N\) (giải thuyết)

Do đó, \(\Delta DEF\backsim\Delta MNP\) (c.g.c)

Do đó, \(\widehat F = \widehat P = 42^\circ \).

Bài 6 trang 71 SGK Toán 8 Chân trời sáng tạo tập 2

a) Cho tam giác \(ABC\) có \(AB = 12cm,AC = 15cm,BC = 18cm\). Trên cạnh \(AB\), lấy điểm \(E\) sao cho \(AE = 10cm\). Trên cạnh \(AC\), lấy điểm \(F\) sao cho \(AF = 8cm\) (hình 18a). Tính độ dài đoan thẳng \(EF\).

b) Trong Hình 18b, cho biết \(FD = FC,BC = 9dm,DE = 12dm,AC = 15dm,MD = 20dm.\)

Chứng minh rằng \(\Delta ABC\backsim\Delta MED\).

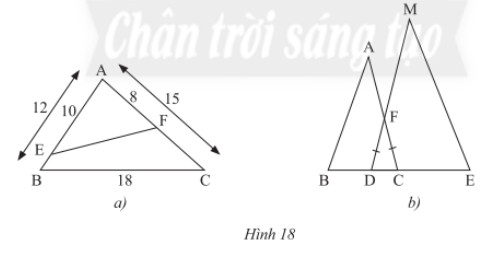
Lời giải:

Bài 7 trang 71 SGK Toán 8 Chân trời sáng tạo tập 2

Trong Hình 19, cho biết \(MN//BC,MB//AC\)

a) Chứng minh rằng \(\Delta BNM\backsim\Delta ABC\)

b) Tính \(\widehat C\)

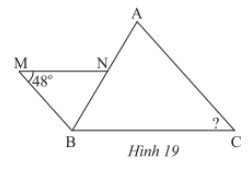
Lời giải:

a) Vì \(MN//BC\) nên \(\widehat {MNB} = \widehat {ABC}\) (hai góc so le trong)

Vì \(MB//AC\) nên \(\widehat {MNB} = \widehat {ABC}\) (hai góc so le trong)

Xét tam giác \(BNM\) tam giác \(ABC\) ta có:

\(\widehat {MNB} = \widehat {ABC}\) (chứng minh trên)

\(\widehat {MNB} = \widehat {ABC}\) (chứng minh trên)

Do đó, \(\Delta BNM\backsim\Delta ABC\) (g.g)

b) Vì \(\Delta BNM\backsim\Delta ABC\) nên \(\widehat M = \widehat C = 48^\circ \) (hai góc tương ứng).

Bài 8 trang 72 SGK Toán 8 Chân trời sáng tạo tập 2

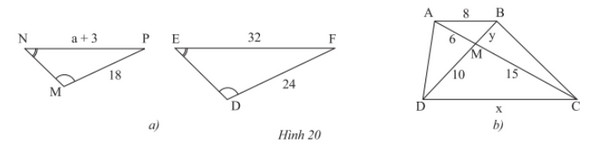
a) Trong Hình 20a, cho biết \(\widehat N = \widehat E,\widehat M = \widehat D,MP = 18m,DF = 24m,\)\(EF = 32m,\)\(NP = a + 3\left( m \right)\). Tìm \(a\).

b) Cho \(ABCD\) là hình thang \(\left( {AB//CD} \right)\) (Hình 20b).

Chứng minh rằng \(\Delta AMB\backsim\Delta CMD\). Tìm \(x,y\).

Lời giải:

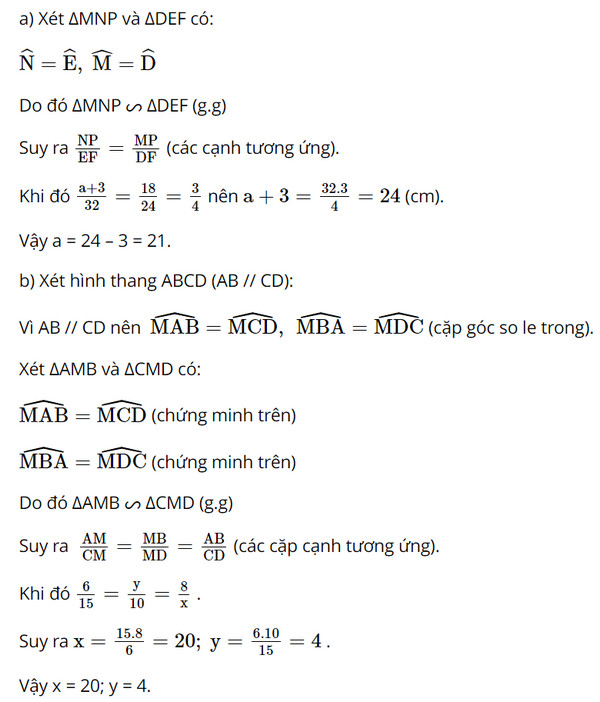
Bài 9 trang 72 SGK Toán 8 Chân trời sáng tạo tập 2

a) Trong Hình 21a, cho biết \(\widehat {HOP} = \widehat {HPE},\widehat {HPO} = \widehat {HEP},OH = 6cm\) và \(HE = 4cm\). Tính độ dài đoạn thẳng \(HP\).

b) Trong Hình 21b, cho biết \(\widehat {AME} = \widehat {AFM}\). Chứng minh rằng \(A{M^2} = AE.AF\).

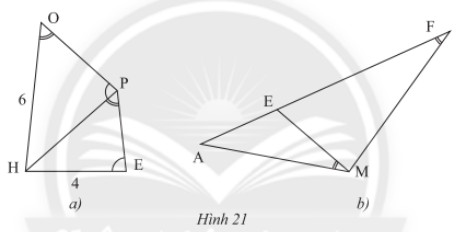
Lời giải:

a) Xét tam giác \(OPH\) tam giác \(PEH\) ta có:

\(\widehat {HOP} = \widehat {HPE}\) (giả thuyết)

\(\widehat {OPH} = \widehat {PEH}\) (giả thuyết)

Do đó, \(\Delta OPH\backsim\Delta PEH\) (g.g)

Suy ra, \(\frac{{PH}}{{EH}} = \frac{{OH}}{{PH}} \Rightarrow P{H^2} = OH.EH = 4.6 \Rightarrow P{H^2} = 24 \Leftrightarrow PH = \sqrt {24}  = 2\sqrt 6 \).

Vậy \(PH = 2\sqrt 6 \).

b) Xét tam giác \(AME\) tam giác \(AFM\) ta có:

\(\widehat {AME} = \widehat {AFM}\) (giả thuyết)

\(\widehat A\) chung

Do đó, \(\Delta AME\backsim\Delta AFM\) (g.g)

Suy ra, \(\frac{{AM}}{{AF}} = \frac{{AE}}{{AM}} \Rightarrow A{M^2} = AF.AE\) (điều phải chứng minh).

Bài 10 trang 72 SGK Toán 8 Chân trời sáng tạo tập 2

Đường đi và khoảng cách từ nhà anh Thanh (điểm \(M\)) đến công ty (điểm \(N\)) được thể hiện trong Hình 22. Hãy tìm con đường ngắn nhất để đi từ nhà anh Thanh đến công ty.

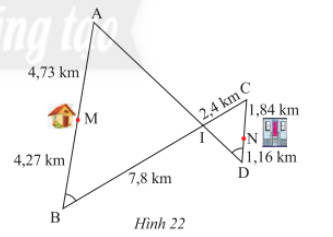
Lời giải:

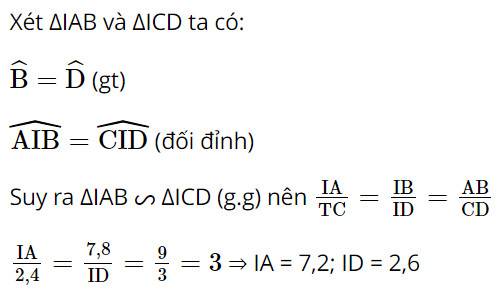
Quãng đường đi từ M → A → I là: 4,73 + 7,2 = 11,93 (km)

Quãng đường đi từ M → B → I là: 4,27 + 7,8 = 12,07 (km)

Quãng đường đi từ I → C → N là: 2,4 + 1,84 = 4,24 (km)

Quãng đường đi từ I → D → N là: 2,6 + 1,16 = 3,76 (km)

Vậy quãng đường ngắn nhất để đi từ nhà của anh Thanh đến công ty là M → A → I → D → N với độ dài 15,69 km.

Giaibaitap.me