Bài 1 trang 90 SGK Toán 8 Chân trời sáng tạo tập 2

Trong hộp có 5 quả bóng có kích thước và khối lượng giống nhau và được đánh số lần lượt là 5; 8; 10; 13; 16. Lấy ngẫu nhiên 1 quả bóng từ hộp. Tính xác suất  của các biến cố:

\(A\): “Số ghi trên quả bóng là số lẻ”.

\(B\): “Số ghi trên quả bóng chia hết cho 3”.

\(C\): “Số ghi trên quả bóng lớn hơn 4”.

Lời giải:

Các quả bóng có kích thước và khối lượng bằng nhau nên có khả năng xảy ra bằng nhau.

Có 2 kết quả thuận lợi cho biến cố A là: 5; 13.

Xác suất của biến cố A là: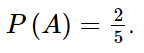 

Có 0 kết quả thuận lợi cho biến cố B hay biến cố B là biến cố không thể suy ra P(B) = 0.

Có 5 kết quả thuận lợi cho biến cố C là: 5; 8; 10; 13; 16. Hay C là biến cố chắc chắn nên P(C) = 1.

Bài 2 trang 90 SGK Toán 8 Chân trời sáng tạo tập 2

Một hộp chứ 3 viên bi xanh, 4 viên bi đỏ và 5 viên bi vàng có kích thước và khối lượng giống nhau. Lấy ra ngẫu nhiên 1 viên bi từ hộp. Tính xác suất của các biến cố:

\(A\): “Viên bi lấy ra có màu xanh”.

\(B\): “Viên bi lấy ra không có màu đỏ”.

Lời giải:

Vì 3 viên bi xanh, 4 viên bi đỏ và 5 viên b vàng có kích thước và khối lượng như nhau nên 12 kết quả của phép thử có khả năng xảy ra bằng nhau.

- Biến cố \(A\) xảy ra khi ta lấy được viên bi màu xanh nên có 3 kết quả thuận lợi cho \(A\). Xác suất của biến có \(A\) là:

\(P\left( A \right) = \frac{3}{{12}} = \frac{1}{4}\).

- Biến cố \(B\) xảy ra khi ta lấy được viên bi không có màu đỏ nên viên bi lấy được có thể có màu xanh hoặc màu vàng. Do đó, có 8 kết quả thuận lợi cho \(B\). Xác suất của biến có \(B\) là:

\(P\left( B \right) = \frac{8}{{12}} = \frac  {2}{3}\).

Bài 3 trang 91 SGK Toán 8 Chân trời sáng tạo tập 2

Trong hộp có 10 tấm thẻ cùng loại, trên mỗi tấm thẻ có ghi một số tự nhiên. Lấy ra ngẫu nhiên 1 thẻ từ hộp. Biết rằng xác suất lấy được thẻ ghi số chẵn gấp 4 lần xác suất lấy được thẻ ghi số lẻ. Hỏi trong hộp có bao nhiêu thẻ ghi số lẻ?

Lời giải:

Gọi số thẻ ghi số lẻ trong hộp là n (n ∈ ℕ, n ≤ 10).

Khi đó, xác suất tấm thẻ lấy ra ghi số lẻ là: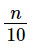 

Số thẻ ghi số chẵn trong hộp là 10 – n.

Khi đó, xác suất tấm thẻ lẩy ra ghi số chẵn là: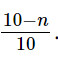 

Vì xác suất lấy được thẻ chẵn gấp 4 lần xác suất lấy được thẻ lẻ nên ta có:

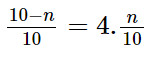
10 – n = 4n

5n = 10

n = 2 (thỏa mãn)

Vậy trong hộp có 2 thẻ ghi số lẻ.

Bài 4 trang 91 SGK Toán 8 Chân trời sáng tạo tập 2

Số lượng học sinh tham gia Câu lạc bộ Cờ vua của một trường được biểu diễn ở biểu đồ sau:

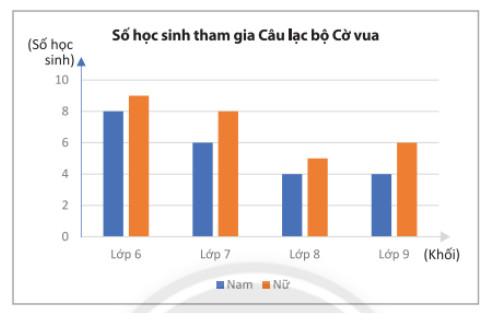
Chọn ngẫu nhiên 1 học sinh trong Câu lạc bộ Cờ vua của trường đó. Tính xác suất các biến cố:

\(A\): “Học sinh được chọn là nữ”.

\(B\): “Học sinh được chọn học lớp 8”.

\(C\): “Học sinh được chọn là nam và không học lớp 7”.

Lời giải:

Tổng số học sinh tham gia câu lạc bộ là:

\(8 + 9 + 6 + 8 + 4 + 5 + 4 + 6 = 50\) (học sinh)

- Biến cố \(A\) xảy ra khi bạn học sinh chọn được là nữ.

Số học sinh nữ tham gia câu lạc bộ là:

\(9 + 8 + 5 + 6 = 28\) (học sinh)

Xác suất của biến có \(A\) là:

\(P\left( A \right) = \frac{{28}}{{50}} = \frac{{14}}{{25}}\)

- Biến cố \(B\) xảy ra khi bạn học sinh chọn được là học sinh lớp 8.

Số học sinh lớp 8 trong câu lạc bộ là:

\(4 + 5 = 9\)(học sinh)

Xác suất của biến có \(B\) là:

\(P\left( B \right) = \frac{9}{{50}}\)

- Biến cố \(C\) xảy ra khi bạn học sinh chọn được là nam và không học lớp 7.

Số học sinh câu lạc bộ là nam và không học lớp 7 là:

\(8 + 4 + 4 = 16\)

Xác suất của biến có \(C\) là:

\(P\left( C \right) = \frac{{16}}{{50}} = \frac{8}{{25}}\)

Bài 5 trang 91 SGK Toán 8 Chân trời sáng tạo tập 2

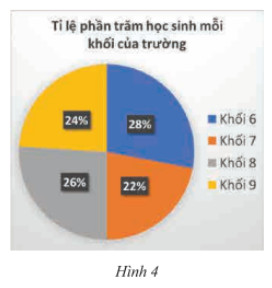
Một trường trung học có sở có 600 học sinh. Tỉ lệ phần trăm học sinh mỗi khối được cho bởi biểu đồ trong Hình 4. Chọn ngẫu nhiên một học sinh trong trường để dự phỏng vấn. Biết rằng mọi học sinh của trường đều có khả năng được lựa chọn như nhau.

a) Tính xác suất của biến cố “Học sinh được chọn thuộc khối 9”.

b) Tính xác suất của biến cố “Học sinh được chọn không thuộc khối 6”.

Lời giải:

a) Số học sinh thuộc khối 9 là: 24% . 600 = 144 (học sinh)

Xác suất của biến cố "Học sinh được chọn thuộc khối 9" là: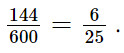 

b) Số học sinh thuộc khối 6 là: 28% . 600 = 168 (học sinh)

Số học sinh không thuộc khối 6 là: 600 – 168 = 432 (học sinh)

Xác suất của biến cố "Học sinh được chọn không thuộc khối 6" là: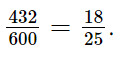 

Giaibaitap.me