Bài 1 trang 71 SGK Toán 8 Chân trời sáng tạo tập 1

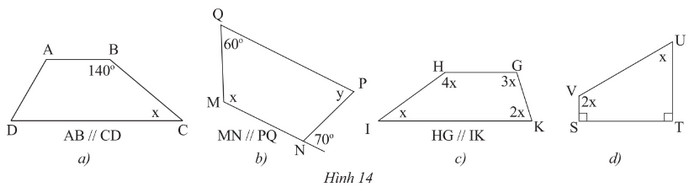
Tìm \(x\) và \(y\) ở các hình sau.

Lời giải:

a) Vì \(AB\) // \(CD\) (gt) suy ra:

\(\widehat B + \widehat C = 180^\circ \) (cặp góc trong cùng phía)

\(\begin{array}{l}140^\circ  + x = 180^\circ \\x = 40^\circ \end{array}\)

b) Vì \(MN\) // \(PQ\) (gt)

\( \Rightarrow \widehat M + \widehat Q = 180^\circ \) (trong cùng phía)

\(\begin{array}{l}x + 60^\circ  = 180^\circ \\x = 120^\circ \end{array}\)

Vì \(MN\) // \(PQ\) (gt)

\( \Rightarrow \widehat P = \widehat N = 70^\circ \) (so le trong)

c) Xét tứ giác \(IHGK\) ta có:

\(\begin{array}{l}\widehat H + \widehat G + \widehat I + \widehat K = 360^\circ \\4x + 3x + 2x + x = 360^\circ \\10x = 360^\circ \\x = 360^\circ :10 = 36^\circ \end{array}\)

d) Xét tứ giác \(UVST\) ta có:

\(\widehat U + \widehat V + \widehat S + \widehat T = 360^\circ \)

\(\begin{array}{l}x + 2x + 90^\circ  + 90^\circ  = 360^\circ \\3x + 180^\circ  = 360^\circ \\3x = 180^\circ \\x = 60^\circ \end{array}\)

Bài 2 trang 71 SGK Toán 8 Chân trời sáng tạo tập 1

Cho tứ giác \(ABCD\) có \(AB = AD\), \(BD\) là tia phân giác của góc \(B\). Chứng minh rằng \(ABCD\) là hình thang.

Lời giải:

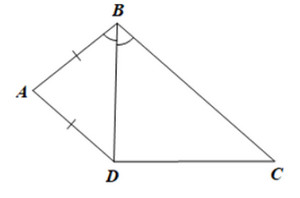
Xét DABD có AB = AD nên là tam giác cân tại A

Mà hai góc này ở vị trí so le trong nên AD // BC.

Xét tứ giác ABCD có AD // BC nên là hình thang.

Vậy ABCD là hình thang.

Bài 3 trang 72 SGK Toán 8 Chân trời sáng tạo tập 1

Cho tam giác nhọn \(ABC\) có \(AH\) là đường cao. Tia phân giác của góc \(B\) cắt \(AC\) tại \(M\). Từ \(M\) kẻ đường thẳng vuông góc với \(AH\) và cắt \(AB\) tại \(N\). Chứng minh rằng:

a) Tứ giác \(BCMN\) là hình thang

b) \(BN = MN\)

Lời giải: 

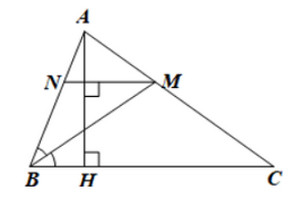
a) Ta có:

\(NM \bot AH\) (gt)

\(BC \bot AH\) (gt)

Suy ra \(NM\) // \(BC\)

Suy ra \(BNMC\) là hình thang

b) Vì \(NM\) // \(BC\) (cmt)

Suy ra \(\widehat {{\rm{NMB}}} = \widehat {{\rm{MBC}}}\) (so le trong)

Mà \(\widehat {{\rm{MBN}}} = \widehat {{\rm{MBC}}}\) (do \(MB\) là phân giác)

Suy ra \(\widehat {{\rm{MBN}}} = \widehat {{\rm{NMB}}}\)

Suy ra \(\Delta MNB\) cân tại \(N\)

Suy ra \(BN = NM\)

Bài 4 trang 72 SGK Toán 8 Chân trời sáng tạo tập 1

Cho tam giác \(ABC\) vuông tại \(A\) (\(AB < AC\)). Tia phân giác của góc \(B\) cắt \(AC\) tại \(D\). Trên \(BC\) lấy điểm\(E\) sao cho \(BE = BA\).

a) Chứng minh rằng \(\Delta ABD = \Delta EBD\)

b) Kẻ đường cao \(AH\) của tam giác \(ABC\). Chứng minh rằng tứ giác \(ADEH\) là hình thang vuông.

c) Gọi \(I\) là giao điểm của \(AH\) với \(BD\), đường thẳng \(EI\) cắt \(AB\) tại \(F\). Chứng minh rằng tứ giác \(ACEF\) là hình thang vuông.

Lời giải: 

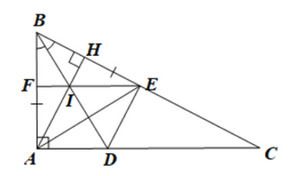
a) Xét \(\Delta ABD\) và \(\Delta EBD\) ta có:

\(BA = BE\) (gt)

\(\widehat {{\rm{ABD}}} = \widehat {{\rm{ EBD}}}\) (do \(BD\) là phân giác)

\(BD\) chung

Suy ra \(\Delta ABD = \Delta EBD\) (c-g-c)

b) Vì \(\Delta ABD = \Delta EBD\) (cmt)

Suy ra \(\widehat {{\rm{BAD}}} = \widehat {{\rm{BED}}} = 90^\circ \) (hai góc tương ứng)

Suy ra \(DE \bot BC\)

Mà \(AH \bot BC\) (gt)

Suy ra \(AH\) // \(DE\)

Suy ra \(ADEH\) là hình thang

Mà \(\widehat {{\rm{DEB}}} = 90\) (cmt)

Suy ra \(ADEH\) là hình thang vuông

c) 

Gọi \(K\) là giao điểm của \(AE\) và \(AD\)

Suy ra \(BK\) là phân giác của \(\widehat {{\rm{ABC}}}\)

Mà \(\Delta ABE\) cân tại \(B\) (do \(BA = BE\) )

Suy ra \(BK\) cũng là đường cao

Xét \(\Delta ABE\) có hai đường cao \(BK\) và \(AH\) cắt nhau tại \(I\)

Suy ra \(I\) là trực tâm của \(\Delta ABE\)

Suy ra \(EF \bot AB\)

Mà \(AC \bot AB\) (do \(\Delta ABC\) vuông tại \(A\))

Suy ra \(AC\) // \(EF\)

Suy ra \(ACEF\) là hình thang

Mà \(\widehat {{\rm{CAE}}} = 90^\circ \)(gt)

Suy ra \(ACEF\) là hình thang vuông

Bài 5 trang 72 SGK Toán 8 Chân trời sáng tạo tập 1

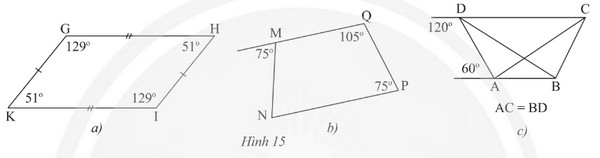
Tứ giác nào trong Hình 15 là hình thang cân?

Lời giải:

• Hình 15a):

Ta thấy hai góc kề một đáy của tứ giác GHIK có số đo là 51° và 129° không bằng nhau.

Do đó tứ giác GHIK không phải là hình thang cân.

• Hình 15b):

Mà hai góc này ở vị trí đồng vị nên MQ // NP.

Tứ giác MNPQ có MQ // NP nên là hình thang.

Tứ giác ABCD có DC // AB và AC = BD nên là hình thang cân.

Bài 6 trang 72 SGK Toán 8 Chân trời sáng tạo tập 1

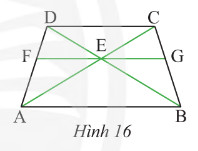
Cho hình thang cân \(ABCD\) có \(AB\) // \(CD\). Qua gia điểm \(E\) của \(AC\) và \(BD\), ta vẽ đường thẳng song song với \(AB\) và cắt \(AD\), \(BC\) lần lượt tại \(F\) và \(G\) (Hình 16). Chứng minh rằng \(EG\) là tia phân giác của góc \(CEB\).

Lời giải:

Vì \(EG\) // \(AB\) (gt)

suy ra \(\widehat {{\rm{CEG}}} = \widehat {{\rm{CAB}}}\) (đồng vị) và \(\widehat {{\rm{GEB}}} = \widehat {{\rm{EBA}}}\) (1)

Xét \(\Delta CAB\) và \(\Delta DBA\) ta có:

\(AC = BD\) (tính chất hình thang cân)

\(BC = AD\) (tính chất hình thang cân)

\(AB\) chung

Suy ra \(\Delta CAB = \Delta DBA\) (c-c-c)

Suy ra \(\widehat {{\rm{CAB}}} = \widehat {{\rm{EAB}}}\) (2)

Từ (1) và (2) suy ra \(\widehat {{\rm{CEG}}} = \widehat {{\rm{GEB}}}\)

Suy ra \(EG\) là phân giác của \(\widehat {{\rm{CEB}}}\)

Bài 7 trang 72 SGK Toán 8 Chân trời sáng tạo tập 1

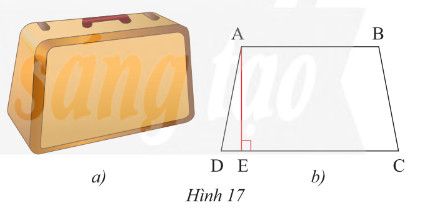
Mặt bên của một chiếc vali (Hình 17a) có dạng hình thang cân và được vẽ lại như Hình 17b. Biết hình thang đó có độ dài đường cao là \(60\)cm, cạnh bên là \(61\)cm và đáy lớn là \(92\)cm. Tính độ dài đáy nhỏ.

Lời giải:

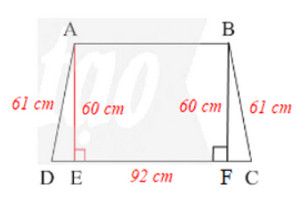
Áp dụng định lí Pythagore vào DADE vuông tại E, ta có:

AD² = AE² + DE²

Suy ra DE² = AD² – AE² = 61² – 60² = 3 721 – 3 600 = 121 = 11²

Do đó DE = 11 cm.

Kẻ BF ⊥ CD, khi đó BF là đường cao của hình thang cân ABCD nên BF = 60 cm.

Xét DADE và DBCF có:

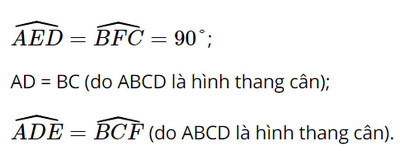
Do đó DADE = DBCF (cạnh huyền – góc nhọn)

Suy ra DE = CF = 11 cm (hai cạnh tương ứng).

Mà DE + EF + CF = DC

Nên EF = DC – DE – CF = 92 – 11 – 11 = 70 cm.

Tương tự Vận dụng 4, trang 71, Sách giáo khoa Toán 8, tập một, ta dễ dàng chứng minh được AB = EF = 70 cm.

Vậy độ dài đáy nhỏ của hình thang cân là 70 cm.

Giaibaitap.me