Bài 1 trang 39 SGK Toán 8 Chân trời sáng tạo tập 1

Thực hiện các phép nhân phân thức sau:

a) \(\dfrac{{4y}}{{3{x^2}}} \cdot \dfrac{{5{x^3}}}{{2{y^3}}}\)                 

b) \(\dfrac{{{x^2} - 2x + 1}}{{{x^2} - 1}} \cdot \dfrac{{{x^2} + x}}{{x - 1}}\)                       

c) \(\dfrac{{2x + {x^2}}}{{{x^2} - x + 1}} \cdot \dfrac{{3{x^3} + 3}}{{3x + 6}}\)

Lời giải:

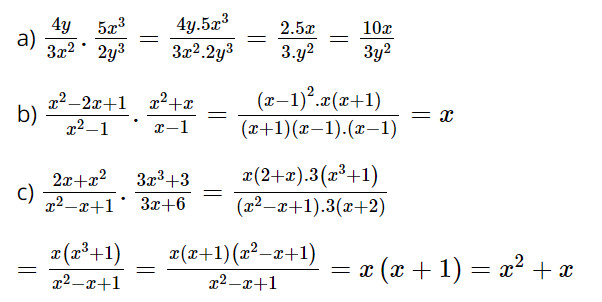
Bài 2 trang 39 SGK Toán 8 Chân trời sáng tạo tập 1

Thực hiện các phép chia phân thức sau:

a) \(\dfrac{{5x}}{{4{y^3}}}:\left( { - \dfrac{{{x^4}}}{{20y}}} \right)\)                 

b) \(\dfrac{{{x^2} - 16}}{{x + 4}} :\dfrac{{2x - 8}}{x}\)                     

c) \(\dfrac{{2x + 6}}{{{x^3} - 8}}:\dfrac{{{{\left( {x + 3} \right)}^3}}}{{2x - 4}}\)  

Lời giải:

a)

\(\dfrac{{5x}}{{4{y^3}}}:\left( { - \dfrac{{{x^4}}}{{20y}}} \right)\) \( = \dfrac{{5x}}{{4{y^3}}} \cdot \dfrac{{ - 20y}}{{{x^4}}} = \dfrac{{ - 100xy}}{{4{x^4}{y^3}}} = \dfrac{{ - 25}}{{{x^3}{y^2}}}\)

b)

\(\dfrac{{{x^2} - 16}}{{x + 4}} :\dfrac{{2x - 8}}{x}\) \( = \dfrac{{\left( {x - 4} \right)\left( {x + 4} \right)}}{{x + 4}} \cdot \dfrac{x}{{2x - 8}} = \dfrac{{\left( {x - 4} \right)\left( {x + 4} \right)}}{{x + 4}} \cdot \dfrac{x}{{2\left( {x - 4} \right)}} = \dfrac{x}{2}\)

c)

\(\dfrac{{2x + 6}}{{{x^3} - 8}}:\dfrac{{{{\left( {x + 3} \right)}^3}}}{{2x - 4}}\)  \( = \dfrac{{2\left( {x + 3} \right)}}{{\left( {x - 2} \right)\left( {{x^2} + 2x + 4} \right)}} \cdot \dfrac{{2\left( {x - 2} \right)}}{{{{\left( {x + 3} \right)}^3}}} = \dfrac{4}{{{{\left( {x + 3} \right)}^2}\left( {{x^2} + 2x + 4} \right)}}\)

Bài 3 trang 39 SGK Toán 8 Chân trời sáng tạo tập 1

Tính:

a) \(\dfrac{{4{x^2} + 2}}{{x - 2}} \cdot \dfrac{{3x + 2}}{{x - 4}} \cdot \dfrac{{4 - 2x}}{{2{x^2} + 1}}\) 

b) \(\dfrac{{x + 3}}{x} \cdot \dfrac{{x + 2}}{{{x^2} + 6x + 9}}:\dfrac{{{x^2} - 4}}{{{x^2} + 3x}}\)

Lời giải: 

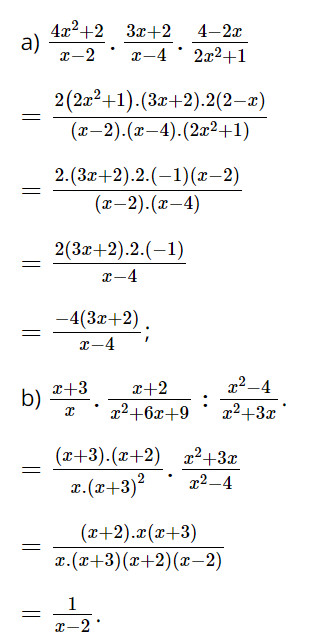
Bài 4 trang 39 SGK Toán 8 Chân trời sáng tạo tập 1

Tính:

a) \(\left( {\dfrac{{1 - x}}{x} + {x^2} - 1} \right):\dfrac{{x - 1}}{x}\)       

b) \(\left( {\dfrac{1}{{{x^2}}} - \dfrac{1}{x}} \right) \cdot \dfrac{{{x^2}}}{y} + \dfrac{x}{y}\)                

c) \(\dfrac{3}{x} - \dfrac{2}{x}:\dfrac{1}{x} + \dfrac{1}{x} \cdot \dfrac{{{x^2}}}{3}\)

Lời giải: 

a)

\(\left( {\dfrac{{1 - x}}{x} + {x^2} - 1} \right):\dfrac{{x - 1}}{x}\) \( = \left( { - \dfrac{{x - 1}}{x} + \dfrac{{\left( {{x^2} - 1} \right)x}}{x}} \right) \cdot \dfrac{x}{{x - 1}} = \dfrac{{ - \left( {x - 1} \right) + x\left( {x - 1} \right)\left( {x + 1} \right)}}{x} \cdot \dfrac{x}{{x - 1}} = \dfrac{{\left( {x - 1} \right)\left[ {1 - x\left( {x + 1} \right)} \right]}}{x} \cdot \dfrac{x}{{x - 1}}\)

\( = 1 - x\left( {x + 1} \right) = 1 - {x^2} - x\)  

b)

\(\left( {\dfrac{1}{{{x^2}}} - \dfrac{1}{x}} \right) \cdot \dfrac{{{x^2}}}{y} + \dfrac{x}{y}\)

\(\begin{array}{l} = \left( {\dfrac{1}{{{x^2}}} - \dfrac{x}{{{x^2}}}} \right) \cdot \dfrac{{{x^2}}}{y} + \dfrac{x}{y}\\ = \dfrac{{1 - x}}{{{x^2}}} \cdot \dfrac{{{x^2}}}{y} + \dfrac{x}{y}\\ = \dfrac{{1 - x}}{y} + \dfrac{x}{y}\\ = \dfrac{1}{y}\end{array}\)

c)

\(\dfrac{3}{x} - \dfrac{2}{x}:\dfrac{1}{x} + \dfrac{1}{x} \cdot \dfrac{{{x^2}}}{3}\)

\(\begin{array}{l} = \dfrac{3}{x} - \dfrac{2}{x} \cdot \dfrac{x}{1} + \dfrac{1}{x} \cdot \dfrac{{{x^2}}}{3}\\ = \dfrac{3}{x} - 2 + \dfrac{x}{3}\\ = \dfrac{9}{{3x}} - \dfrac{{6x}}{{3x}} + \dfrac{{{x^2}}}{{3x}}\\ = \dfrac{{{x^2} - 6x + 9}}{{3x}}\end{array}\)

Bài 5 trang 39 SGK Toán 8 Chân trời sáng tạo tập 1

Tâm đạp xe từ nhà tới câu lạc bộ câu cá có quãng đường dài \(15\)km với tốc độ \(x\)(km/h). Lượt về thuận chiều gió nên tốc độ nhanh hơn lượt đi \(4\)km/h.

a) Viết biểu thức biểu thị tổng thời gian \(T\) hai lượt đi và về.

b) Viết biểu thức biểu thị hiệu thời gian \(t\) luợt đi đối với lượt về.

c) Tính \(T\) và \(t\) với \(x = 10\)

Lời giải:

Giaibaitap.me