A. TRẮC NGHIỆM

Bài 1 trang 40 SGK Toán 8 Chân trời sáng tạo tập 1

Biểu thức nào sau đây không phải là đa thức

A. \(\sqrt 2 {x^2}y\)              

B. \( - \dfrac{1}{2}x{y^2} + 1\)                    

C. \(\dfrac{1}{{2z}}x + y\)                 

D. 0

Lời giải:

Đáp án đúng là: C

Biểu thức 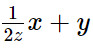 không phải là đa thức vì có phép chia giữa hai biến x và z.

Bài 2 trang 40 SGK Toán 8 Chân trời sáng tạo tập 1

Đơn thức nào sau đây đồng dạng với đơn thức \( - 2{x^3}y\)?

A. \(\dfrac{1}{3}{x^2}yx\)                 

B. \(2{x^3}yz\)           

C. \( - 2{x^3}z\)                     

D. \(3x{y^3}\)

Lời giải:

Đáp án A vì:

\(\dfrac{1}{3}{x^2}yx = \dfrac{1}{3}{x^3}y\)

Bài 3 trang 40 SGK Toán 8 Chân trời sáng tạo tập 1

Biểu thức nào sau đây không phải là đa thức bậc 4?

A. \(2{x^2}yz\)                       

B. \({x^4} - \dfrac{1}{3}{x^3}{y^2}\)                      

C. \({x^2}y + xyzt\)               

D. \({x^4} - {2^5}\)

Lời giải: 

Đáp án đúng là: B

Hai hạng tử của đa thức 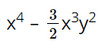 có bậc lần lượt là 4 và 5 nên bậc của đa thức này bằng 5. Vậy biểu thức này không phải là đa thức bậc 4.

Bài 4 trang 40 SGK Toán 8 Chân trời sáng tạo tập 1

Biểu thức nào sau đây không phải là phân thức?

A. \({x^2}y + y\)                    

B. \(\dfrac{{3xy}}{{\sqrt 2 z}}\)                   

C. \(\dfrac{{\sqrt x }}{2}\)                            

D. \(\dfrac{{a + b}}{{a - b}}\)                      

Lời giải: 

Đáp án C vì \(\sqrt x \) không phải đa thức

Bài 5 trang 40 SGK Toán 8 Chân trời sáng tạo tập 1

Kết quả của phép nhân \((x + y - 1)(x + y + 1)\) là:

A. \({x^2} - 2xy + {y^2} + 1\)

B. \({x^2} + 2xy + {y^2} - 1\)

C. \({x^2} - 2xy + {y^2} - 1\)

D. \({x^2} + 2xy + {y^2} + 1\)

Lời giải:

Đáp án đúng là: B

Ta có: (x + y – 1)(x + y + 1)

        = (x + y)² – 1²

        = x² + 2xy + y² – 1.

Bài 6 trang 40 SGK Toán 8 Chân trời sáng tạo tập 1

Khi phân tích đa thức \(P = {x^4} - 4{x^2}\) thành nhân tử thì được:

A. \(P = {x^2}(x - 2)(x + 2)\)   

B. \(P = x(x - 2)(x + 2)\)

C. \(P = {x^2}(x - 4)(x + 4)\)  

D. \(P = x(x - 4)(x + 2)\)

Lời giải:

Ta có;

\(P = {x^4} - 4{x^2} = {x^2}.\left( {{x^2} - 4} \right) = {x^2}\left( {x - 2} \right)\left( {x + 2} \right)\)

Đáp án A

Bài 7 trang 40 SGK Toán 8 Chân trời sáng tạo tập 1

Kết quả của phép trừ \(\dfrac{2}{{{{(x + 1)}^2}}} - \dfrac{1}{{{x^2} - 1}}\) là:

A. \(\dfrac{{3 - x}}{{(x - 1){{(x + 1)}^2}}}\)

B. \(\dfrac{{x - 3}}{{(x - 1){{(x + 1)}^2}}}\)

C. \(\dfrac{{x - 3}}{{{{(x + 1)}^2}}}\)

D. \(\dfrac{1}{{(x - 1){{(x + 1)}^2}}}\)   

Lời giải:

Đáp án đúng là: A

Ta có: P = x⁴ – 4x²

              = (x²)² – (2x)²

              = (x² + 2x)(x² – 2x)

              = x(x + 2).x(x – 2)

              = x²(x – 2)(x + 2).

Bài 8 trang 40 SGK Toán 8 Chân trời sáng tạo tập 1

Kết quả của phép trừ \(\dfrac{2}{{{{(x + 1)}^2}}} - \dfrac{1}{{{x^2} - 1}}\) là:

A. \(\dfrac{{3 - x}}{{(x - 1){{(x + 1)}^2}}}\)

B. \(\dfrac{{x - 3}}{{(x - 1){{(x + 1)}^2}}}\)

C. \(\dfrac{{x - 3}}{{{{(x + 1)}^2}}}\)

D. \(\dfrac{1}{{(x - 1){{(x + 1)}^2}}}\)   

Lời giải:

Ta có:

\(\dfrac{2}{{{{(x + 1)}^2}}} - \dfrac{1}{{{x^2} - 1}}\)\( = \dfrac{2}{{{{\left( {x + 1} \right)}^2}}} - \dfrac{1}{{\left( {x + 1} \right)\left( {x - 1} \right)}} = \dfrac{{2\left( {x - 1} \right)}}{{{{\left( {x + 1} \right)}^2}\left( {x - 1} \right)}} - \dfrac{{\left( {x + 1} \right)}}{{{{\left( {x + 1} \right)}^2}\left( {x - 1} \right)}}\)

\( = \dfrac{{2x - 2 - x - 1}}{{{{\left( {x + 1} \right)}^2}\left( {x - 1} \right)}} = \dfrac{{x - 3}}{{{{\left( {x + 1} \right)}^2}\left( {x - 1} \right)}}\)

Đáp án B

Bài 9 trang 40 SGK Toán 8 Chân trời sáng tạo tập 1

Khi phân tích đa thức \(R = 4{x^2} - 4xy + {y^2}\) thành nhân tử thì được:

A. \(R = {(x + 2y)^2}\)   

B. \(R = {(x - 2y)^2}\)

C. \(R = {(2x + y)^2}\) 

D. \(R = {(2x - y)^2}\)

Lời giải:

Đáp án đúng là: D

Ta có R = 4x² – 4xy + y²

             = (2x)² – 2.2x.y + y²

             = (2x – y)²

Bài 10 trang 40 SGK Toán 8 Chân trời sáng tạo tập 1

Khi phân tích đa thức \(S = {x^6} - 8\) thành nhân tử thì được:

A. \(S = \left( {{x^2} + 2} \right)\left( {{x^4} - 2{x^2} + 4} \right)\)

B. \(S = \left( {{x^2} - 2} \right)\left( {{x^4} - 2{x^2} + 4} \right)\)

C. \(S = \left( {{x^2} - 2} \right)\left( {{x^4} + 2{x^2} + 4} \right)\)

D. \(S = \left( {x - 2} \right)\left( {{x^4} + 2{x^2} + 4} \right)\)

Lời giải:

\(S = {x^6} - 8 = {\left( {{x^2}} \right)^3} - {2^3} = \left( {{x^2} - 2} \right)\left( {{x^4} + 2{x^2} + 4} \right)\)

Đáp án C

B. TỰ LUẬN

Bài 11 trang 41 SGK Toán 8 Chân trời sáng tạo tập 1

Tính giá trị của đa thức \(P = x{y^2}z - 2{x^2}y{z^2} + 3yz + 1\) khi \(x = 1\); \(y =  - 1\); \(z = 2\)

Lời giải:

Thay x = 1, y = –1 và z = 2 vào đa thức P ta được:

P = 1.(–1)².2 – 2.1².(–1).2² + 3.(–1).2 + 1

   = 2 + 8 – 6 + 1

   = 5.

Vậy P = 5 khi x = 1, y = –1, z = 2.

Bài 12 trang 41 SGK Toán 8 Chân trời sáng tạo tập 1

Cho đa thức \(P = 3{x^2}y - 2x{y^2} - 4xy + 2\).

a) Tìm đa thức \(Q\) sao cho \(Q - P =  - 2{x^3}y + 7{x^2}y + 3xy\)

b) Tìm đa thức \(M\) sao cho \(P + M = 3{x^2}{y^2} - 5{x^2}y + 8xy\)

Lời giải:

a) \(Q - P =  - 2{x^3}y + 7{x^2}y + 3xy\)

\(Q =  - 2{x^3}y + 7{x^2}y + 3xy + P\)

\(Q =  - 2{x^3}y + 7{x^2}y + 3xy + 3{x^2}y - 2x{y^2} - 4xy + 2\)

\(Q =  - 2{x^3}y + 10{x^2}y - 2x{y^2} - xy + 2\)

b) \(P + M = 3{x^2}{y^2} - 5{x^2}y + 8xy\)

\(M = 3{x^2}{y^2} - 5{x^2}y + 8xy - P\)

\(M = 3{x^2}{y^2} - 5{x^2}y + 8xy - \left( {3{x^2}y - 2x{y^2} - 4xy + 2} \right)\)

\(\begin{array}{l}M = 3{x^2}{y^2} - 5{x^2}y + 8xy - 3{x^2}y + 2x{y^2} + 4xy - 2\\M = 3{x^2}{y^2} - 8{x^2}y + 2x{y^2} + 12xy - 2\end{array}\)

Bài 13 trang 41 SGK Toán 8 Chân trời sáng tạo tập 1

Thực hiện các phép tính sau:

a) \({x^2}y\left( {5xy - 2{x^2}y - {y^2}} \right)\)

b) \(\left( {x - 2y} \right)\left( {2{x^2} + 4xy} \right)\)

Lời giải:

a) x²y(5xy – 2x²y – y²)

= x²y.5xy – x²y.2x²y  – x²y.y²

= 5x³y² – 2x⁴y² – x²y³.

b) (x – 2y)(2x² + 4xy)

= x(2x² + 4xy) – 2y.(2x² + 4xy)

= 2x³ + 4x²y – 4x²y – 8xy²

= 2x³ – 8xy².

Bài 14 trang 41 SGK Toán 8 Chân trời sáng tạo tập 1

Thực hiện các phép tính sau:

a) \(18{x^4}{y^3}:12{\left( { - x} \right)^3}y\)

b) \({x^2}{y^2} - 2x{y^3}:\left( {\dfrac{1}{2}x{y^2}} \right)\)

Lời giải:

a) \(18{x^4}{y^3}:12{\left( { - x} \right)^3}y\)

\( = -(18:12).({x^4}:{x^3}).({y^3}:y)\)

\( =  - 1,5{x}{y^2}\)

b) \({x^2}{y^2} - 2x{y^3}:\left( {\dfrac{1}{2}x{y^2}} \right)\) \( = {x^2}{y^2} - 4y\)

Bài 15 trang 41 SGK Toán 8 Chân trời sáng tạo tập 1

Tính:

a) \(\left( {2x + 5} \right)\left( {2x - 5} \right) - \left( {2x + 3} \right)\left( {3x - 2} \right)\)

b) \({\left( {2x - 1} \right)^2} - 4\left( {x - 2} \right)\left( {x + 2} \right)\)

Lời giải:

a) (2x + 5)(2x – 5) – (2x + 3)(3x – 2)

= 4x² – 25 – (6x² – 4x + 9x – 6)

= 4x² – 25 – (6x² + 5x – 6)

= 4x² – 25 – 6x² – 5x + 6

= (4x² – 6x²) – 5x + (– 25 + 6)

= –2x² – 5x – 19.

b) (2x – 1)² – 4(x – 2)(x + 2)

= 4x² – 4x + 1 – 4(x² – 4)

= 4x² – 4x + 1 – 4x² + 16

= (4x² – 4x²) – 4x + (1 + 16)

= – 4x + 17.

Bài 16 trang 41 SGK Toán 8 Chân trời sáng tạo tập 1

Phân tích các đa thức sau thành nhân tử:

a) \({\left( {x - 1} \right)^2} - 4\) 

b) \(4{x^2} + 12x + 9\) 

c) \({x^3} - 8{y^6}\)

d) \({x^5} - {x^3} - {x^2} + 1\) 

e) \( - 4{x^3} + 4{x^2} + x - 1\) 

f) \(8{x^3} + 12{x^2} + 6x + 1\)

Lời giải:

a) \({\left( {x - 1} \right)^2} - 4\) \( = \left( {x - 1 - 2} \right)\left( {x - 1 + 2} \right) = \left( {x - 3} \right)\left( {x + 1} \right)\)

b) \(4{x^2} + 12x + 9\) \( = {\left( {2x} \right)^2} + 2.2x.3 + {3^2} = {\left( {2x + 3} \right)^2}\)

c) \({x^3} - 8{y^6}\) \( = {x^3} - {\left( {2{y^2}} \right)^3} = \left( {x - 2{y^2}} \right)\left( {{x^2} + 2x{y^2} + 4{y^4}} \right)\)

d) \({x^5} - {x^3} - {x^2} + 1\) \( = {x^3}\left( {{x^2} - 1} \right) - \left( {{x^2} - 1} \right) = \left( {{x^2} - 1} \right)\left( {{x^3} - 1} \right) = \left( {x - 1} \right)\left( {x + 1} \right)\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)\)\( = {\left( {x - 1} \right)^2}\left( {x + 1} \right)\left( {{x^2} + x + 1} \right)\)

e) \( - 4{x^3} + 4{x^2} + x - 1\) \( =  - 4{x^2}\left( {x - 1} \right) + \left( {x - 1} \right) = \left( {x - 1} \right)\left( { - 4{x^2} + 1} \right) = \left( {x - 1} \right)\left( {1 - 2x} \right)\left( {1 + 2x} \right)\)

f) \(8{x^3} + 12{x^2} + 6x + 1\) \( = {\left( {2x + 1} \right)^3}\)

Bài 17 trang 41 SGK Toán 8 Chân trời sáng tạo tập 1

 Cho \(x + y = 3\) và \(xy = 2\). Tính \({x^3} + {y^3}\)

Lời giải:

Ta có: x³ + y³

= (x + y)(x² – xy + y²)

= (x + y)[(x² + 2xy + y²) – 3xy]

= (x + y)[(x² + 2xy + y²) – 3xy]

= (x + y)[(x + y)² – 3xy]

Thay x + y = 3 và xy = 2 vào đa thức trên ta có:

x³ + y³ = 3.(3² – 3.2) = 3.(9 – 6) = 3.3 = 9.

Vậy với x + y = 3 và xy = 2 thì x³ + y³ = 9.

Bài 18 trang 41 SGK Toán 8 Chân trời sáng tạo tập 1

Thực hiện các phép tính sau:

a) \(\dfrac{{2{x^2} - 1}}{{x - 2}} + \dfrac{{ - {x^2} - 3}}{{x - 2}}\)                       

b) \(\dfrac{x}{{x + y}} + \dfrac{y}{{x - y}}\)    

c) \(\dfrac{1}{{x - 1}} - \dfrac{2}{{{x^2} - 1}}\)

d) \(\dfrac{{x + 2}}{{{x^2} + xy}} - \dfrac{{y - 2}}{{xy + {y^2}}}\)                                  

e) \(\dfrac{1}{{2{x^2} - 3x}} - \dfrac{1}{{4{x^2} - 9}}\)                     

g) \(\dfrac{{2x}}{{9 - {x^2}}} + \dfrac{1}{{x - 3}} - \dfrac{1}{{x + 3}}\)      

Lời giải:

a)

\(\dfrac{{2{x^2} - 1}}{{x - 2}} + \dfrac{{ - {x^2} - 3}}{{x - 2}}\)

\( = \dfrac{{{x^2} - 4}}{{x - 2}}\)

\(\begin{array}{l} = \dfrac{{\left( {x - 2} \right)\left( {x + 2} \right)}}{{x - 2}}\\ = x + 2\end{array}\) 

b)

\(\dfrac{x}{{x + y}} + \dfrac{y}{{x - y}}\)

\(\begin{array}{l} = \dfrac{{x(x - y)}}{{(x + y)(x - y)}} + \dfrac{{y(x + y)}}{{(x - y)(x + y)}}\\ = \dfrac{{{x^2} - xy + xy + {y^2}}}{{\left( {x - y} \right)\left( {x + y} \right)}}\\ = \dfrac{{{x^2} + {y^2}}}{{{x^2} - {y^2}}}\end{array}\)

c)

\(\dfrac{1}{{x - 1}} - \dfrac{2}{{{x^2} - 1}}\)\( = \dfrac{{x + 1}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} - \dfrac{2}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = \dfrac{{x - 1}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = \dfrac{1}{{x + 1}}\)

d)

\(\dfrac{{x + 2}}{{{x^2} + xy}} - \dfrac{{y - 2}}{{xy + {y^2}}}\)          

\(\begin{array}{l} = \dfrac{{x + 2}}{{x(x + y)}} - \dfrac{{y - 2}}{{y(x + y)}}\\ = \dfrac{{\left( {x + 2} \right)y}}{{xy\left( {x + y} \right)}} - \dfrac{{\left( {y - 2} \right)x}}{{xy\left( {x + y} \right)}}\\ = \dfrac{{xy + 2y}}{{xy\left( {x + y} \right)}} - \dfrac{{xy - 2x}}{{xy\left( {x + y} \right)}}\\ = \dfrac{{2y + 2x}}{{xy\left( {x + y} \right)}}\\ = \dfrac{{2\left( {x + y} \right)}}{{xy\left( {x + y} \right)}}\\ = \dfrac{2}{{xy}}\end{array}\)

e)

\(\dfrac{1}{{2{x^2} - 3x}} - \dfrac{1}{{4{x^2} - 9}}\)    

\(\begin{array}{l} = \dfrac{1}{{x\left( {2x - 3} \right)}} - \dfrac{1}{{\left( {2x - 3} \right)\left( {2x + 3} \right)}}\\ = \dfrac{{2x + 3}}{{x\left( {2x - 3} \right)\left( {2x + 3} \right)}} - \dfrac{x}{{x\left( {2x - 3} \right)\left( {2x + 3} \right)}}\\ = \dfrac{{x + 3}}{{x\left( {4{x^2} - 9} \right)}}\end{array}\)

g)

\(\dfrac{{2x}}{{9 - {x^2}}} + \dfrac{1}{{x - 3}} - \dfrac{1}{{x + 3}}\)    

\(\begin{array}{l} = \dfrac{{ - 2x}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} + \dfrac{1}{{x - 3}} - \dfrac{1}{{x + 3}}\\ = \dfrac{{ - 2x}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} + \dfrac{{x + 3}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} - \dfrac{{x - 3}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\\ = \dfrac{{ - 2x + 6}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\\ = \dfrac{{ - 2\left( {x - 3} \right)}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\\ = \dfrac{{ - 2}}{{x + 3}}\end{array}\)

Bài 19 trang 41 SGK Toán 8 Chân trời sáng tạo tập 1

Thực hiện các phép tính sau:

a) \(\dfrac{{8y}}{{3{x^2}}} \cdot \dfrac{{9{x^2}}}{{4{y^2}}}\)

b) \(\dfrac{{3x + {x^2}}}{{{x^2} + x + 1}} \cdot \dfrac{{3{x^3} - 3}}{{x + 3}}\)

c) \(\dfrac{{2{x^2} + 4}}{{x - 3}} \cdot \dfrac{{3x + 1}}{{x - 1}}:\dfrac{{{x^2} + 2}}{{6 - 2x}}\)

d) \(\dfrac{{2{x^2}}}{{3{y^3}}}:\left( { - \dfrac{{4{x^3}}}{{21{y^2}}}} \right)\)

e) \(\dfrac{{2x + 10}}{{{x^3} - 64}}:\dfrac{{{{\left( {x + 5} \right)}^2}}}{{2x - 8}}\)

f) \(\dfrac{1}{{x + y}}\left( {\dfrac{{x + y}}{{xy}} - x - y} \right) - \dfrac{1}{{{x^2}}}:\dfrac{y}{x}\)      

Lời giải:

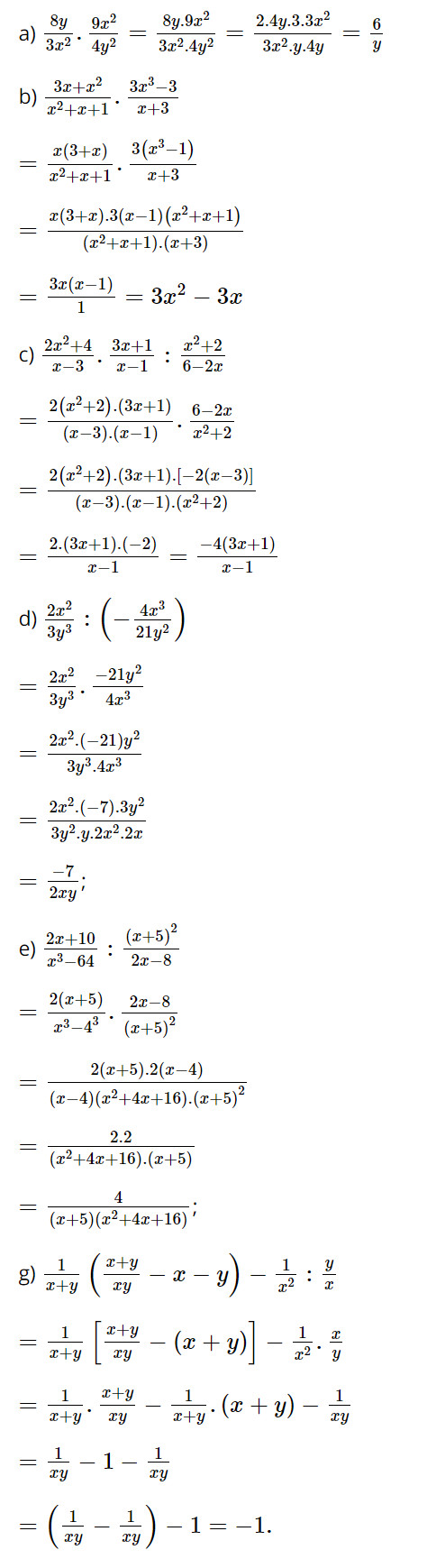
Bài 20 trang 41 SGK Toán 8 Chân trời sáng tạo tập 1

Hôm qua thanh long được bán với giá \(a\) đồng mỗi ki-lô-gam. Hôm nay, người ta đã giảm giá \(1000\) đồng cho mỗi ki-lô-gam thanh long. Với cùng số tiền \(b\) đồng thì hôm nay mua được nhiều hơn bao nhiêu ki-lô-gam thanh long so với hôm qua?

Lời giải:

Giá 1kg thanh long sau khi giảm là: \(x - 1000\) (đồng)

Với số tiền đó, hôm qua người đó mua được số thanh long là: \(\dfrac{b}{a}\) (kg)

Với số tiền đó, hôm nay người đó mua được số thanh long là: \(\dfrac{b}{{a - 1000}}\)  (kg)

Hôm nay mua nhiều hơn hôm qua số kg là:

\(\dfrac{b}{{a - 1000}} - \dfrac{b}{a} = \dfrac{{ba}}{{\left( {a - 1000} \right)a}} - \dfrac{{b\left( {a - 1000} \right)}}{{\left( {a - 1000} \right)a}} = \dfrac{{ba - ba + 1000b}}{{a\left( {a - 1000} \right)}} = \dfrac{{1000b}}{{{a^2} - 1000a}}\) (kg)

Bài 21 trang 41 SGK Toán 8 Chân trời sáng tạo tập 1

Trên một dòng sông, một con thuyền đi xuôi dòng với tốc độ \(x + 3\) km/h và đi ngược dòng với tốc độ \(x - 3\) km/h (\(x > 3)\).

a) Xuất phát từ bến A, thuyền đi xuôi dòng trong 4 giờ, rồi đi ngược dòng trong 2 giờ. Tính quãng đường thuyền đã đi. Lúc này thuyền cách bến A bao xa?

b) Xuất phát từ bến A, thuyền đi xuôi dòng đến bến B cách bến A \(15\)km, nghỉ \(30\) phút, rồi quay về bến A. Sau bao lâu kể từ lúc xuất phát thì thuyền quay về đến bến A?

Lời giải:

a) Thuyền đi xuôi dòng trong 4 giờ được quãng đường là: 4(x + 3) (km).

Thuyền đi ngược dòng trong 2 giờ được quãng đường là: 2(x – 3) (km).

Quãng đường thuyền đã đi là:

4(x + 3) + 2(x – 3) = 4x + 12 + 2x – 6 = 6x + 6 (km).

Lúc này thuyền cách bến A là:

4(x + 3) – 2(x – 3) = 4x + 12 – 2x + 6 = 2x + 18 (km). 

Giaibaitap.me