Bài 1 trang 87 SGK Toán 8 Chân trời sáng tạo tập 1

Cho Hình 14. Tìm \(x\).

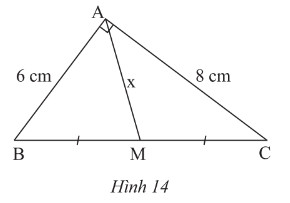
Lời giải:

Áp dụng định lí Pythagore vào \(\Delta ABC\) vuông tại \(A\), ta có:

\(B{C^2} = A{B^2} + A{C^2} = {6^2} + {8^2} = 100 = {10^2}\)

Suy ra \(BC = 10\) (cm).

Xét \(\Delta ABC\) vuông tại \(A\) có \(AM\) là đường trung tuyến ứng với cạnh huyền nên \(AM\) bằng nửa cạnh huyền \(BC\).

Do đó \(x = AM = \frac{1}{2}BC = \frac{1}{2}.10 = 5\) (cm)

Vậy \(x = 5\) cm

Bài 2 trang 87 SGK Toán 8 Chân trời sáng tạo tập 1

Cho Hình 15. Vẽ thêm điểm \(P\) để tứ giác \(MNPQ\) là hình chữ nhật

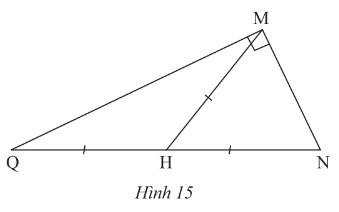
Lời giải:

Cách vẽ:

• Lấy điểm P đối xứng với điểm M qua H.

• Nối PN, PQ. Ta được hình chữ nhật MNPQ.

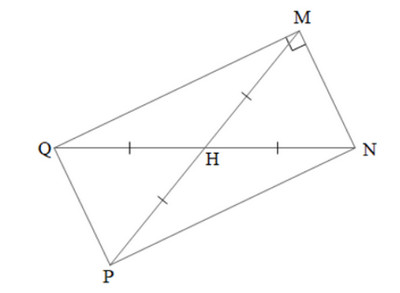
Giải thích:

Tứ giác MNPQ có H là trung điểm của hai đường chéo MP và NQ nên là hình bình hành.

Lại có 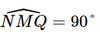 nên hình bình hành MNPQ là hình chữ nhật.

Bài 3 trang 87 SGK Toán 8 Chân trời sáng tạo tập 1

Cho tam giác \(ABC\) có đường cao \(AH\). Gọi \(I\) là trung điểm của \(AC\), \(E\) là điểm đối xứng với \(H\) qua \(I\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(HC\), \(CE\). Các đường thẳng \(AM\), \(AN\) cắt \(HE\) tại \(G\) và \(K\).

a) Chứng minh tứ giác \(AHCE\) là hình chữ nhật

b) Chứng minh \(HG = GK = KE\)

Lời giải: 

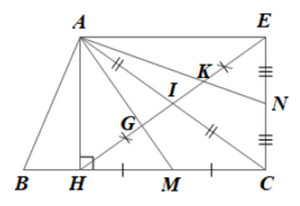
a) Do \(E\) là điểm đối xứng với \(H\) qua \(I\) nên \(I\) là trung điểm của \(HE\) hay \(HI = EI\)

Tứ giác \(AHCE\) có hai đường chéo \(AC\) và \(HE\) cắt nhau tại trung điểm \(I\) (gt) nên là hình bình hành.

Lại có \(\widehat {AHC} = 90^\circ \) (do \(AH\) là đường cao) nên hình bình hành \(AHCE\) là hình chữ nhật.

b) Xét \(\Delta AHC\) có \(AM\), \(HI\) là hai đường trung tuyến cắt nhau tại \(G\) nên \(G\) là trọng tâm của \(\Delta AHC\).

Suy ra: \(HG = \frac{2}{3}HI;\;IG = \frac{1}{2}HG\)

Chứng minh tưng tự đối với \(\Delta AEC\) có \(K\) là trọng tâm của \(\Delta AEC\)

Suy ra: \(EK = \frac{2}{3}EI\) và \(IK = \frac{1}{2}EK\)

Ta có: \(HG = \frac{2}{3}HI;\;EK = \frac{2}{3}EI\) mà \(HI = EI\)

Suy ra \(HG = EK = \frac{2}{3}EI\)

Mà \(EI = \frac{1}{2}EH\)

Suy ra \(HG = EK = \frac{1}{3}HE\)

Suy ra \(GK = HE - HG - KE = HE - \frac{1}{3}HE - \frac{1}{3}HE = \frac{1}{3}HE\)

Vậy \(HG = GK = KE\)

Bài 4 trang 87 SGK Toán 8 Chân trời sáng tạo tập 1

Cho tam giác \(ABC\) vuông tại \(A\) (\(AB < AC\). Gọi \(D\) là trung điểm của \(BC\). Vẽ \(DE\) // \(AB\), vẽ \(DF\) // \(AC\) \((E \in AC\); \(F \in AB)\). Chứng minh rằng:

a) Tứ giác \(AEDF\) là hình chữ nhật

b) Tứ giác \(BFED\) là hình bình hành

Lời giải: 

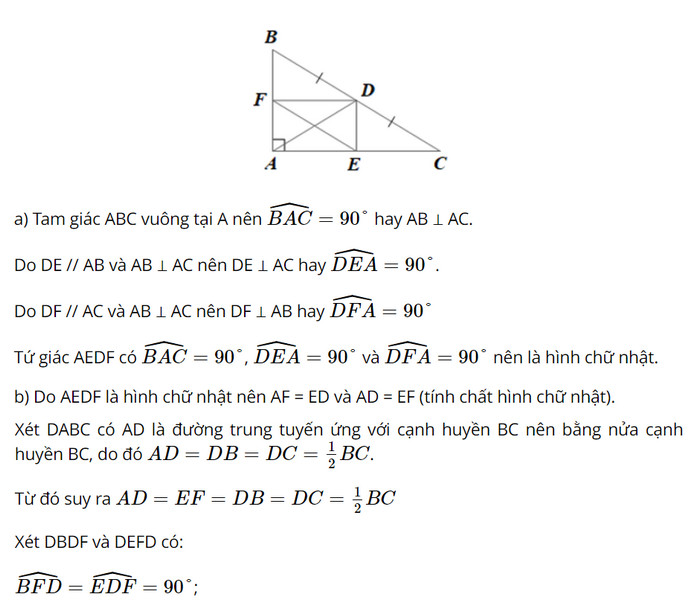
BD = EF (chứng minh trên);

DF là cạnh chung.

Do đó DBDF = DEFD (cạnh huyền – cạnh góc vuông).

Suy ra FB = DE (hai cạnh tương ứng).

Xét tứ giác BFED có FB = DE và FB // DE (do AB // DE) nên là hình bình hành.

Bài 5 trang 87 SGK Toán 8 Chân trời sáng tạo tập 1

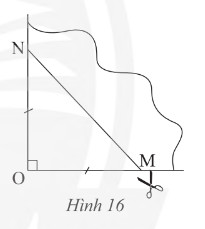
Lấy một tờ giấy, gấp làm tư để có một góc vuông như triong Hình 16, dùng kéo cắt theo đường \(MN\) sao cho \(OM = ON\). Mở phần giấy cắt được ra ta được một tứ giác. Tứ giác đó là hình gì. Giải thích kết luận của em.

Lời giải:

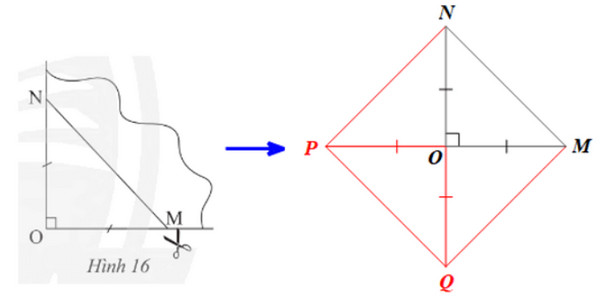
Vì \(OM = ON = OP = OQ\) nên \(O\) là trung điểm của \(NQ\) và \(MP\) và \(MP = NQ\)

Xét tứ giác \(MNPQ\) có hai đường chéo \(NQ\) và \(MP\) cắt nhau tại trung điểm \(O\) (cmt)

Suy ra \(MNPQ\) là hình bình hành

Mà \(MP = NQ\) (cmt) nên \(MNPQ\) là hình chữ nhật

Lại có \(MP \bot NQ\) (gt) nên \(MNPQ\) là hình vuông

Giaibaitap.me