Bài 1 trang 35 SGK Toán 8 Chân trời sáng tạo tập 2

Trong Hình 4, cho biết các viên bi có cùng khối lượng là \(x\left( g \right)\) và cân bằng. Viết phương trình biểu diễn liên hệ giữa khối lượng của các vật ở hai đĩa cân.

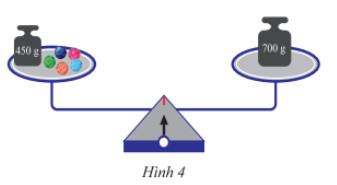
Lời giải:

Các viên bi có cùng khối lượng là x (g). Khi đó:

• Khối lượng các vật ở đĩa cân bên trái là: 450 + 5x (g)

• Khối lượng của vật ở đĩa cân bên phải là: 700 (g)

Vì cân thăng bằng nên ta có phương trình:

450 + 5x = 700.

Vậy phương trình biểu diễn liên hệ giữa khối lượng các vật ở trên hai đĩa cân là 450 + 5x = 700.

Bài 2 trang 36 SGK Toán 8 Chân trời sáng tạo tập 2

Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn? Xác định các hệ số a và b của phương trình bậc nhất một ẩn đó.

a) \(7x + \dfrac{4}{7} = 0\);

b) \(\dfrac{3}{2}y - 5 = 4\);

c) \(0t + 6 = 0\);

d) \({x^2} + 3 = 0\).

Lời giải:

a) Phương trình \(7x + \dfrac{4}{7} = 0\) là phương trình bậc nhất một ẩn vì có dạng \(ax + b = 0\) với \(a\) và \(b\) là các hệ số đã cho và \(a \ne 0\), \(x\) là ẩn số.

Khi đó, \(a = 7;b = \dfrac{4}{7}\).                      

b) \(\dfrac{3}{2}y - 5 = 4\)

\(\dfrac{3}{2}y - 5 - 4 = 0\)

\(\dfrac{3}{2}y - 9 = 0\)

Phương trình \(\dfrac{3}{2}y - 9 = 0\) là phương trình bậc nhất một ẩn vì có dạng \(ay + b = 0\) với \(a\) và \(b\) là các hệ số đã cho và \(a \ne 0\), \(y\) là ẩn số.

Khi đó, \(a = \dfrac{3}{2};b =  - 9\)

c) Phương trình \(0t + 6 = 0\) không là phương trình bậc nhất một ẩn.

Mặc dù phương trình đã cho có dạng   \(at + b = 0\) với \(a\) và \(b\) là các hệ số đã cho nhưng \(a = 0\).    

d) Phương trình \({x^2} + 3 = 0\) không là phương trình bậc nhất một ẩn vì không có dạng \(ax + b = 0\) với \(a\) và \(b\) là các hệ số đã cho và \(a \ne 0\), \(x\) là ẩn số (do có \({x^2}\)).

Bài 3 trang 36 SGK Toán 8 Chân trời sáng tạo tập 2

Giải các phương trình sau:

a) \(5x - 30 = 0\);

b) \(4 - 3x = 11\);

c) \(3x + x + 20 = 0\);

d) \(\dfrac{1}{3}x + \dfrac{1}{2} = x + 2\).

Lời giải:

a) 5x – 30 = 0

5x = 30

x = 30 : 5

x = 6

Vậy phương trình đã cho có nghiệm là x = 6.

b) 4 – 3x = 11

–3x = 11 – 4

–3x = 9

x = 9 : (–3)

x = –3

Vậy phương trình đã cho có nghiệm là: x = −3.

c) 3x + x + 20 = 0

4x = –20

x = –20 : 4

x = –5

Vậy phương trình đã cho có nghiệm là: x = −5. 

Bài 4 trang 36 SGK Toán 8 Chân trời sáng tạo tập 2

Giải các phương trình sau:

a) \(8 - \left( {x - 15} \right) = 2.\left( {3 - 2x} \right)\);

b) \( - 6\left( {1,5 - 2u} \right) = 3\left( { - 15 + 2u} \right)\);

c) \({\left( {x + 3} \right)^2} - x\left( {x + 4} \right) = 13\);

d) \(\left( {y + 5} \right)\left( {y - 5} \right) - {\left( {y - 2} \right)^2} = -5\).

Lời giải:

a) 8 − (x − 15) = 2(3 − 2x)

8 − x + 15 = 6 − 4x

−x + 4x = 6 − 15 − 8

3x = −17

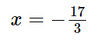
Vậy phương trình đã cho có nghiệm là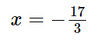 

b) −6(1,5 − 2u) = 3(−15 + 2u)

−9 + 12u = −45 + 6u

12u − 6u = −45 + 9

6u = −36

u = −6

c) (x + 3)² − x(x + 4) = 13

x² + 6x + 9 − x² − 4x = 13

6x − 4x = 13 − 9

2x = 4

x = 2

Vậy phương trình đã cho có nghiệm là x = 2.

d) (y + 5)(y − 5) − (y − 2)² = −5

y² – 25 − y² + 4y – 4 = −5

4y = −5 + 4 + 25

4y = 24

y = 6

Vậy phương trình đã cho có nghiệm là y = 6.

Bài 5 trang 36 SGK Toán 8 Chân trời sáng tạo tập 2

Giải các phương trình sau: 

a) \(\dfrac{{5x - 3}}{4} = \dfrac{{x + 2}}{3}\); 

b) \(\dfrac{{9x + 5}}{6} = 1 - \dfrac{{6 + 3x}}{8}\); 

c) \(\dfrac{{2\left( {x + 1} \right)}}{3} - \dfrac{1}{2} = \dfrac{{1 + 3x}}{4}\); 

d) \( \frac {x+3}{5} - \frac{2}{3}x = \frac{3}{10}\)

Lời giải:

a) 

\(\dfrac{{5x - 3}}{4} = \dfrac{{x + 2}}{3}\)

\(\dfrac{{\left( {5x - 3} \right).3}}{{4.3}} = \dfrac{{\left( {x + 2} \right).4}}{{3.4}}\)

\(\dfrac{{15x - 9}}{{12}} = \dfrac{{4x + 8}}{{12}}\)

\(15x - 9 = 4x + 8\)

\(15x - 4x = 8 + 9\)

\(11x = 17\)

\(x = 17:11\)

\(x = \dfrac{{17}}{{11}}\)

Vậy phương trình có nghiệm \(x = \dfrac{{17}}{{11}}\).

b) 

\(\dfrac{{\left( {9x + 5} \right).4}}{{6.4}} = \dfrac{{24}}{{24}} - \dfrac{{\left( {6 + 3x} \right).3}}{{8.3}}\)

\(\dfrac{{36x + 20}}{{24}} = \dfrac{{24}}{{24}} - \dfrac{{18 + 9x}}{{24}}\)

\(36x + 20 = 24 - \left( {18 + 9x} \right)\)

\(36x + 20 = 24 - 18 - 9x\)

\(36x + 9x = 24 - 18 - 20\)

\(45x =  - 14\)

\(x = \left( { - 14} \right):45\)

\(x = \dfrac{{ - 14}}{{45}}\)

Vậy phương trình có nghiệm \(x = \dfrac{{ - 14}}{{45}}\).

c)

\(\dfrac{{2\left( {x + 1} \right)}}{3} - \dfrac{1}{2} = \dfrac{{1 + 3x}}{4}\)

\(\dfrac{{2x + 2}}{3} - \dfrac{1}{2} = \dfrac{{1 + 3x}}{4}\)

\(\dfrac{{\left( {2x + 2} \right).4}}{{3.4}} - \dfrac{{1.6}}{{2.6}} = \dfrac{{\left( {1 + 3x} \right).3}}{{4.3}}\)

\(\dfrac{{8x + 8}}{{12}} - \dfrac{6}{{12}} = \dfrac{{3 + 9x}}{{12}}\)

\(8x + 8 - 6 = 3 + 9x\)

\(8x - 9x = 3 - 8 + 6\)

\( - x = 1\)

\(x =  - 1\)

Vậy phương trình có nghiệm \(x =  - 1\).

d) 

\(\dfrac{{x + 3}}{5} - \dfrac{2}{3}x = \dfrac{3}{{10}}\)

\(\dfrac{{\left( {x + 3} \right).6}}{{5.6}} - \dfrac{{2.10}}{{3.10}}x = \dfrac{{3.3}}{{10.3}}\)

\(\dfrac{{6x + 18}}{{30}} - \dfrac{{20x}}{{30}} = \dfrac{9}{{30}}\)

\(6x + 18 - 20x = 9\)

\(6x - 20x = 9 - 18\)

\( - 14x =  - 9\)

\(x = \left( { - 9} \right):\left( { - 14} \right)\)

\(x = \dfrac{9}{{14}}\)

Vậy phương trình có nghiệm \(x = \dfrac{9}{{14}}\).

Bài 6 trang 36 SGK Toán 8 Chân trời sáng tạo tập 2

Tìm \(x\), biết rằng nếu lấy \(x\) trừ đi \(\dfrac{1}{2}\), rồi nhân kết quả với \(\dfrac{1}{2}\) thì được \(\dfrac{1}{8}\).

Lời giải:

Theo bài cho ta có phương trình:

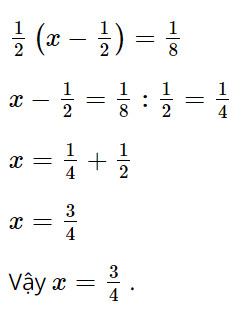
Giaibaitap.me