Bài 1 trang 49 SGK Toán 8 Chân trời sáng tạo tập 2

a) Hãy đo chiều dài và chiều rộng cái bàn học của em và tính tỉ số giữa hai kích thước này.

b) Quãng đường từ Thành phố Hồ Chí Minh đi Mỹ Tho là 70 km, quãng đường từ Thành phố Hồ Chí Minh đi Cà Mau là 350 km. Tính tỉ số giữa hai quãng đường này.

c) Cho biết \(\frac{{AB}}{{CD}} = \frac{3}{5}\) và \(AB = 6cm\). Hãy tính \(CD\).

Lời giải:

a) Chiều dài của cái bàn học của em là \(120cm\); chiều rộng của cái bàn học của em là \(70cm\). Tỉ số giữa chiều dài và chiều rộng của cái bàn là: \(CD:CR = \frac{{CD}}{{CR}} = \frac{{120}}{{70}} = \frac{{12}}{7}\).

b) Tỉ số giữa hai quãng đường từ Thành phố Hồ Chí Minh đi Mỹ Tho và từ Thành phố Hồ Chí Minh đi Cà Mau là: \(70:350 = \frac{{70}}{{350}} = \frac{1}{5}\).

c) Ta có: \(\frac{{AB}}{{CD}} = \frac{3}{5}\) mà \(AB = 6cm \Rightarrow \frac{6}{{CD}} = \frac{3}{5} \Rightarrow CD = \frac{{5.6}}{3} = 10cm\)

Vậy \(CD = 10cm\).

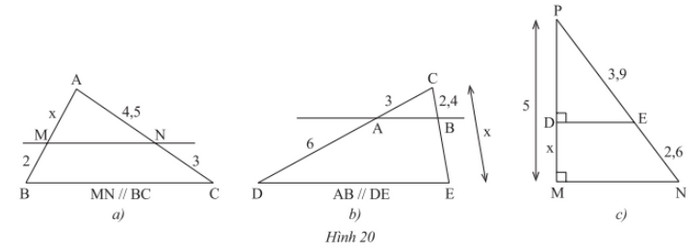
Bài 2 trang 49 SGK Toán 8 Chân trời sáng tạo tập 2

Tìm \(x\) trong Hình 20.

Lời giải:

a) Xét tam giác ABC có MN // BC, theo định lí Thalès, ta có:

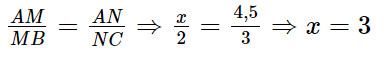
Vậy x = 3.

b) Xét tam giác CDE có AB // DE, theo định lí Thalès, ta có:

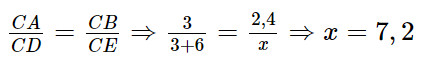
Vậy x = 7,2.

c) Xét tam giác MNP có DE ⊥ MP và MN ⊥ MP nên suy ra DE // MN.

Theo định lí Thalès, ta có:

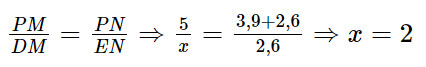
Vậy x = 2.

Bài 3 trang 50 SGK Toán 8 Chân trời sáng tạo tập 2

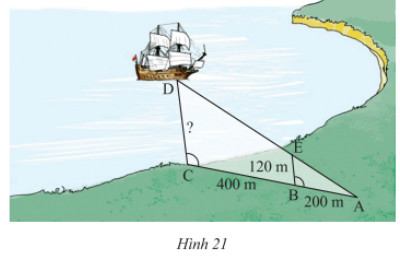
Với số liệu được ghi trên Hình 21. Hãy tính khoảng cách \(CD\) từ con tàu đến trạm quan trắc đặt tại điểm \(C\).

Lời giải:

Ta có \(\widehat {ABE} = \widehat {ACD}\), mà hai góc này ở vị trí đồng vị nên \(BE//CD\).

Ta có: \(AC = AB + BC = 200 + 400 = 600m\)

Xét tam giác \(ACD\) có \(BE//CD\) nên theo hệ quả của định lí Thales ta có:

\(\frac{{AB}}{{AC}} = \frac{{BE}}{{CD}} \Rightarrow \frac{{200}}{{600}} = \frac{{120}}{{CD}}\). Do đó, \(CD = \frac{{120.600}}{{200}} = 360\).

Vậy \(CD = 360m\).

Bài 4 trang 50 SGK Toán 8 Chân trời sáng tạo tập 2

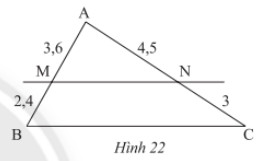
Quan sát Hình 22, chứng minh rằng \(MN//BC\).

Lời giải:

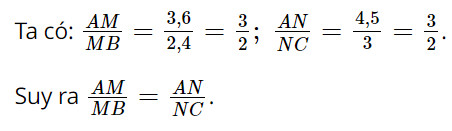
Theo định lí Thalès đảo, ta có: MN // BC.

Bài 5 trang 50 SGK Toán 8 Chân trời sáng tạo tập 2

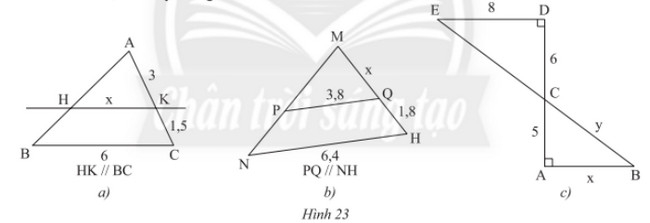
Tính các độ dài \(x,y\) trong Hình 23.

Lời giải:

a) Ta có: \(AC = AK + KC = 3 + 1,5 = 4,5\)

Xét tam giác \(ABC\) có \(HK//BC\) nên theo hệ quả của định lí Thales ta có:

\(\frac{{HK}}{{BC}} = \frac{{AK}}{{AC}} \Rightarrow \frac{x}{6} = \frac{3}{{4,5}}\). Do đó, \(x = \frac{{3.6}}{{4,5}} = 4\).

Vậy \(x = 4\).

b) Ta có: \(MH = MQ + QH = x + 1,8\)

Xét tam giác \(MNH\) có \(PQ//NH\) nên theo hệ quả của định lí Thales ta có:

\(\frac{{PQ}}{{NH}} = \frac{{MQ}}{{MH}} \Rightarrow \frac{{3,8}}{{6,4}} = \frac{x}{{x + 1,8}}\). Do đó, \(6,4x = 3,8.\left( {x + 1,8} \right)\)

\( \Leftrightarrow 6,4x = 3,8x + 6,84\)

\( \Leftrightarrow 6,4x - 3,8x = 6,84\)

\( \Leftrightarrow 2,6x = 6,84\)

\( \Leftrightarrow x = 6,84:2,6\)

\( \Leftrightarrow x = \frac{{171}}{{65}}\).

Vậy \(x = \frac{{171}}{{65}}\).

c) Vì \(\left\{ \begin{array}{l}DE \bot AD\\AB \bot AD\end{array} \right. \Rightarrow DE//AB\) (quan hệ từ vuông góc đến song song).

Xét \(\Delta CDE\) vuông tại \(D\) ta có:

\(E{D^2} + D{C^2} = E{C^2}\) (Định lí Py- ta – go)

\( \Leftrightarrow {8^2} + {6^2} = E{C^2}\)

\( \Leftrightarrow E{C^2} = 100\)

\( \Leftrightarrow EC = 10\)

Xét tam giác \(ABC\) có \(DE//AB\) nên theo hệ quả của định lí Thales ta có:

\(\left\{ \begin{array}{l}\frac{{AC}}{{DC}} = \frac{{AB}}{{ED}} \Rightarrow \frac{5}{6} = \frac{x}{8}\\\frac{{AC}}{{DC}} = \frac{{BC}}{{EC}} \Rightarrow \frac{5}{6} = \frac{y}{{10}}\end{array} \right.\). Do đó, \(\left\{ \begin{array}{l}x = \frac{{5.8}}{6} = \frac{{20}}{3}\\y = \frac{{5.10}}{6} = \frac{{25}}{3}\end{array} \right.\).

Vậy \(x = \frac{{20}}{3};y = \frac{{25}}{3}\).

Bài 6 trang 50 SGK Toán 8 Chân trời sáng tạo tập 2

Quan sát Hình 24, chỉ ra các cặp đường thẳng song song và chứng minh điều ấy.

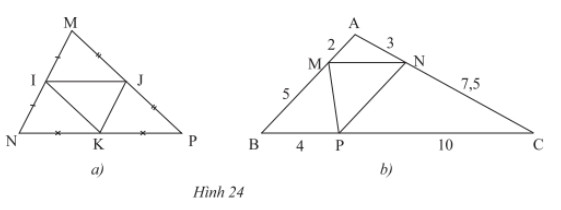
Lời giải:

Theo định lí Thalès đảo ta có: MN // BC.

Bài 7 trang 51 SGK Toán 8 Chân trời sáng tạo tập 2

Cho hình thang \(ABCD\left( {AB//CD} \right)\) có hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\). Chứng minh rằng \(OA.OD = OB.OC\)

Lời giải:

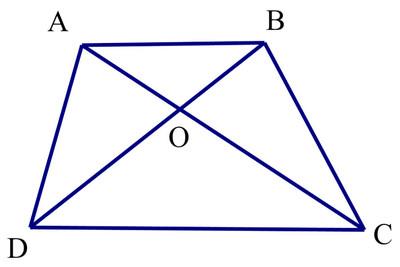
Xét tam giác \(OCD\) có \(AB//CD\) (giả thiết) và \(AB\) cắt \(OC;OD\) lần lượt tại \(A;B\).

Theo hệ quả của định lí Thales ta có:

\(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} = \frac{{AB}}{{CD}} \Rightarrow \frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} \Rightarrow OA.OD = OB.OC\)  (điều phải chứng minh).

Bài 8 trang 51 SGK Toán 8 Chân trời sáng tạo tập 2

Cho hình thang \(ABCD\left( {AB//CD} \right)\). Đường thẳng song song với \(AB\) cắt \(AD, BD, AC\) và \(BC\) theo thứ tự tại các điểm \(M, N, P, Q\).

Chứng minh rằng \(MN = PQ\).

Lời giải:

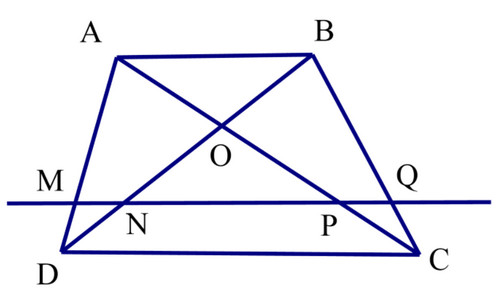
Trong tam giác ADB, ta có: MN // AB (gt)

Trong tam giác ACB, ta có: PQ // AB (gt)

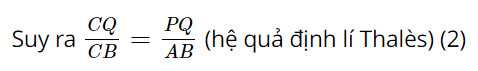
Lại có: NQ // AB (gt)

            AB // CD (gt)

Suy ra NQ // CD

Trong tam giác BDC, ta có: NQ // CD (chứng minh trên)

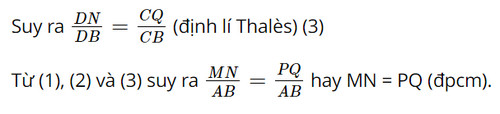
Bài 9 trang 51 SGK Toán 8 Chân trời sáng tạo tập 2

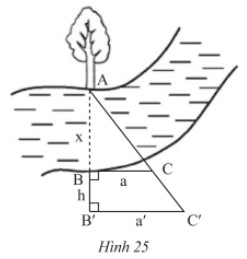
Quan sát Hình 25 và chứng minh: \(x = \frac{{ah}}{{a' - a}}\).

Lời giải:

Vì \(\left\{ \begin{array}{l}BC \bot AB'\\B'C' \bot AB'\end{array} \right. \Rightarrow BC//B'C'\)(quan hệ từ vuông góc đến song song).

- Xét tam giác \(AB'C'\) có \(BC//B'C'\) và \(BC\) cắt \(AB';AC'\) lần lượt tại \(B;C\).

Theo hệ quả của định lí Thales ta có:

\(\frac{{AB}}{{AB'}} = \frac{{BC}}{{B'C'}} \Rightarrow \frac{x}{{x + h}} = \frac{a}{{a'}} \Rightarrow xa' = a\left( {x + h} \right) \Leftrightarrow xa' = ax + ah\) 

\( \Leftrightarrow xa' - ax = ah \Leftrightarrow x\left( {a' - a} \right) = ah \Leftrightarrow x = \frac{{ah}}{{a' - a}}\) (điều phải chứng minh).

Giaibaitap.me