Bài 1 trang 53 SGK Toán 8 Chân trời sáng tạo tập 2

Cho \(MN\) là đường trung bình của mỗi tam giác \(ABC\) trong Hình 9. Hãy tìm giá trị \(x\) trong mỗi hình.

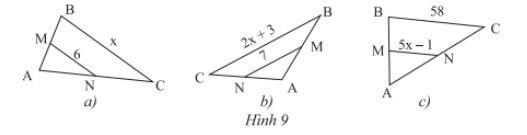
Lời giải:

- Hình a:

Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên theo tính chất đường trung bình ta có:

\(\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}x \Leftrightarrow 6 = \frac{1}{2}x \Leftrightarrow x = 6:\frac{1}{2} = 12\)

- Hình b:

Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên theo tính chất đường trung bình ta có:

\(\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}\left( {2x + 3} \right) \Leftrightarrow 7 = \frac{1}{2}\left( {2x + 3} \right) \Leftrightarrow \left( {2x + 3} \right) = 7:\frac{1}{2} = 14\)

\( \Rightarrow 2x = 14 - 3 \Leftrightarrow 2x = 11 \Leftrightarrow x = 6,5\).

- Hình c

Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên theo tính chất đường trung bình ta có:

\(\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}.58 \Leftrightarrow \left( {5x - 1} \right) = \frac{1}{2}.58\)

\( \Leftrightarrow \left( {5x - 1} \right) = 29 \Leftrightarrow 5x = 30 \Leftrightarrow x = 30:5 \Leftrightarrow x = 6\).

Bài 2 trang 54 SGK Toán 8 Chân trời sáng tạo tập 2

Tính độ dài đoạn \(PQ\) (Hình 10).

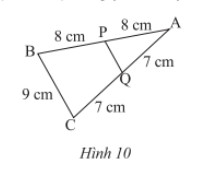
Lời giải:

Xét tam giác ABC có:

AP = PB = 8 cm

AQ = QC = 7 cm

Khi đó, PQ là đường trung bình tam giác ABC.

Bài 3 trang 54 SGK Toán 8 Chân trời sáng tạo tập 2

Cho biết cạnh mỗi ô vuông bằng \(1cm\). Tính độ dài các đoạn \(PQ,PR,RQ,AB,BC,CA\) trong Hình 11.

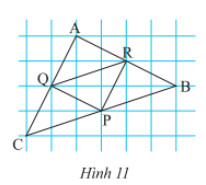
Lời giải:

Đoạn thẳng \(AB\) là đường chéo của hình chữ nhật với chiều dài là \(4cm;\) chiều rộng là \(2cm\). Áp dụng định lí Py – ta – go ta được: \(A{B^2} = {2^2} + {4^2} = 4 + 16 = 20 \Rightarrow AB = \sqrt {20}  = 2\sqrt 5 \)

Đoạn thẳng \(AC\) là đường chéo của hình chữ nhật với chiều dài là \(4cm;\) chiều rộng là \(2cm\). Áp dụng định lí Py – ta – go ta được: \(A{C^2} = {2^2} + {4^2} = 4 + 16 = 20 \Rightarrow AC = \sqrt {20}  = 2\sqrt 5 \)

Đoạn thẳng \(BC\) là đường chéo của hình chữ nhật với chiều dài là \(6cm;\) chiều rộng là \(2cm\). Áp dụng định lí Py – ta – go ta được: \(B{C^2} = {2^2} + {6^2} = 4 + 36 = 40 \Rightarrow BC = \sqrt {40}  = 2\sqrt {10} \)

Từ hình vẽ ta thấy:

\(Q\) là trung điểm của \(AC\);

\(R\) là trung điểm của \(AB\);

\(P\) là trung điểm của \(BC\).

- Vì \(Q\) là trung điểm của \(AC\); \(R\) là trung điểm của \(AB\) nên \(QR\) là đường trung bình của tam giác \(ABC \Rightarrow QR = \frac{1}{2}BC\) (tính chất đường trung bình)

\( \Leftrightarrow QR = \frac{1}{2}.2\sqrt {10}  = \sqrt {10} \left( {cm} \right)\).

- Vì \(Q\) là trung điểm của \(AC\); \(P\) là trung điểm của \(BC\) nên \(QP\) là đường trung bình của tam giác \(ABC \Rightarrow QP = \frac{1}{2}AB\) (tính chất đường trung bình)

\( \Leftrightarrow QP = \frac{1}{2}.2\sqrt 5  = \sqrt 5 \left( {cm} \right)\).

- \(R\) là trung điểm của \(AB\); \(P\) là trung điểm của \(BC\) nên \(RP\) là đường trung bình của tam giác \(ABC \Rightarrow RP = \frac{1}{2}AC\) (tính chất đường trung bình)

\( \Leftrightarrow RP = \frac{1}{2}.2\sqrt 5  = \sqrt 5 \left( {cm} \right)\).

Bài 4 trang 54 SGK Toán 8 Chân trời sáng tạo tập 2

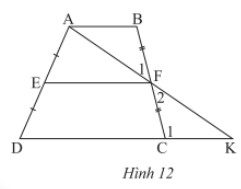
Cho hình thang \(ABCD\left( {AB//CD} \right)\) có \(E\) và \(F\) lần lượt là trung điểm hai cạnh bên \(AD\) và \(BC\). Gọi \(K\)là giao điểm của \(AF\) và \(DC\) (Hình 12).

a) Tam giác \(FBA\) và tam giác \(FCK\) có bằng nhau không? Vì sao?

b) Chứng minh: \(EF//CD//AB\).

c) Chứng minh \(EF = \frac{{AB + CD}}{2}\).

Lời giải:

a) Xét tam giác FBA và FCK ta có:

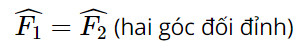
FB = FC (giả thiết)

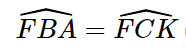 (AB // CD, hai góc so le trong)

Do đó ΔFBA = ΔFCK (g.c.g)

b) ΔFBA = ΔFCK suy ra FA = FK

Xét tam giác ADK có:

EA = ED

FA = FK

Do đó, EF là đường trng bình tam giác ABC.

Suy ra EF // DK

Mà AB // CD nên EF // CD // AB.

c) EF là đường trung bình tam giác ADK.

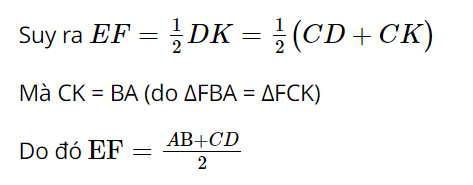
Bài 5 trang 54 SGK Toán 8 Chân trời sáng tạo tập 2

Cho tam giác \(ABC\) nhọn. Gọi \(M,N,P\) lần lượt là trung điểm của \(AB;AC;BC\). Kẻ đường cao \(AH\). Chứng minh rằng tứ giác \(MNPH\) là hình thang cân.

Lời giải:

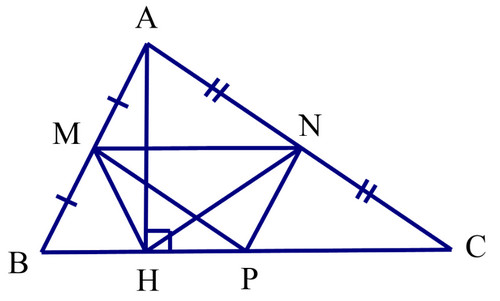
- Vì \(M\) là trung điểm của \(AB;N\) là trung điểm của \(AC\) nên \(MN\) là đường trung bình của tam giác \(ABC\). Do đó, \(MN//BC\) (tính chất đường trung bình).

\( \Rightarrow MN//HP\left( {H;P \in BC} \right)\)

Xét tứ giác \(MNPH\) có: \(MN//HP \Rightarrow \) tứ giác \(MNPH\) là hình thang.

- Vì \(M\) là trung điểm của \(AB;P\) là trung điểm của \(AC\) nên \(MP\) là đường trung bình của tam giác \(ABC\). Do đó, \(MP = \frac{1}{2}AC\) (tính chất đường trung bình) (1).

- Xét tam giác \(AHC\) vuông tại \(H\) có:

\(N\)là trung điểm của \(AC\) nên \(HN = \frac{1}{2}AC\) (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông) (2).

Từ (1) và (2) suy ra \(MP = HN\).

Xét hình thang \(MNPH\) có: \(MP = HN\) (chứng minh trên).

Do đó, hình thang \(MNPH\) là hình thang cân (dấu hiệu nhận biết hình thang cân).

Bài 6 trang 54 SGK Toán 8 Chân trời sáng tạo tập 2

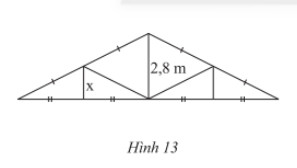
Một mái nhà được vẽ như Hình 13. Tính độ dài \(x\) trong hình mái nhà.

Lời giải:

Xét tam giác ABH có:

AD = BD

BE = EH

Do đó DE là đường trung bình tam giác ABH nên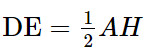 

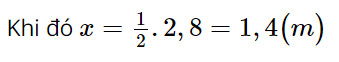
Bài 7 trang 54 SGK Toán 8 Chân trời sáng tạo tập 2

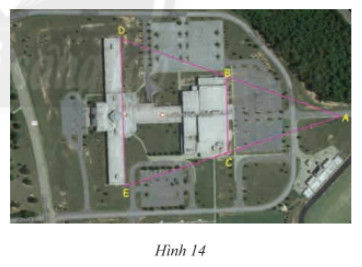
Ảnh chụp từ Google Maps của một trường học được cho trong Hình 14. Hãy tính chiều dài cạnh \(DE\), cho biết \(BC = 232m\) và \(B,C\) lần lượt là trung điểm của \(AD\) và \(AE\).

Lời giải:

Xét tam giác \(ADE\) có:

\(B,C\) lần lượt là trung điểm của \(AD\) và \(AE\)

\( \Rightarrow BC\) là đường trung bình của tam giác \(ADE\).

\( \Rightarrow BC = \frac{1}{2}DE\) (tính chất đường trung bình của tam giác).

\( \Leftrightarrow DE = 2BC = 2.232 = 464\left( m \right)\)

Vậy chiều dài cạnh \(DE\) là \(464m\).

Giaibaitap.me