Bài 1 trang 30 SGK Toán 8 Chân trời sáng tạo tập 1

Trong các biểu thức sau, biểu thức nào là các phân thức?

\(\dfrac{{3x + 1}}{{2x - 1}}\) ; \(2{x^2} - 5x + 3\) ; \(\dfrac{{x + \sqrt x }}{{3x + 2}}\)

Lời giải:

Các biểu thức  \(\dfrac{{3x + 1}}{{2x - 1}}\), \(2{x^2} - 5x + 3\) là phân thức

Biểu thức \(\dfrac{{x + \sqrt x }}{{3x + 2}}\) không là phân thức vì \(\sqrt x \) không là đa thức

Bài 2 trang 30 SGK Toán 8 Chân trời sáng tạo tập 1

Viết điều kiện xác định của các phân thức sau:

a) \(\dfrac{{4x - 1}}{{x - 6}}\)

b) \(\dfrac{{x - 10}}{{x + 3y}}\)

c) \(3{x^2} - x + 7\) 

Lời giải:

a) Điều kiện xác định của phân thức 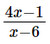là x – 6 ≠ 0, hay x ≠ 6.

b) Điều kiện xác định của phân thức 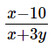 là x + 3y ≠ 0 (nghĩa là tại các giá trị của x và y thỏa mãn x + 3y ≠ 0).

c) Phân thức 3x2 – x + 7 xác định với mọi giá trị x ∈ ℝ.

Bài 3 trang 30 SGK Toán 8 Chân trời sáng tạo tập 1

Tìm giá trị của phân thức:

a) \(A = \dfrac{{3{x^2} + 3x}}{{{x^2} + 2x + 1}}\)  tại \(x =  - 4\)

b) \(B = \dfrac{{ab - {b^2}}}{{{a^2} - {b^2}}}\) tại \(a = 4\), \(b =  - 2\)

Lời giải: 

a) \(A = \dfrac{{3{x^2} + 3x}}{{{x^2} + 2x + 1}} = \dfrac{{3x\left( {x + 1} \right)}}{{{{\left( {x + 1} \right)}^2}}}\)

Điều kiện xác định: \(x \ne  - 1\)

Ta có: \(A = \dfrac{{3{x^2} + 3x}}{{{x^2} + 2x + 1}} = \dfrac{{3x\left( {x + 1} \right)}}{{{{\left( {x + 1} \right)}^2}}} = \dfrac{{3x}}{{x + 1}}\)

Khi \(x =  - 4\) (thỏa mãn điều kiện xác định), ta có:

\(A = \dfrac{{3.\left( { - 4} \right)}}{{ - 4 + 1}} = \dfrac{{ - 12}}{{ - 3}} = 4\)      

Vậy \(A = 4\) khi \(x =  - 4\)

b) Điều kiện xác định: \({a^2} \ne {b^2}\) hay \(a \ne  \pm b\)

Ta có: \(B = \dfrac{{ab - {b^2}}}{{{a^2} - {b^2}}}\)\( = \dfrac{{b\left( {a - b} \right)}}{{\left( {a + b} \right)\left( {a - b} \right)}} = \dfrac{b}{{a + b}}\)

Khi \(a = 4\), \(b =  - 2\) (thỏa mãn điều kiện xác định), ta có:

\(B = \dfrac{{ - 2}}{{4 + \left( { - 2} \right)}} = \dfrac{{ - 2}}{2} =  - 1\)

Vậy \(B =  - 1\) khi \(a = 4\), \(b =  - 2\)

Bài 4 trang 30 SGK Toán 8 Chân trời sáng tạo tập 1

Mỗi cặp phân thức sau có bằng nhau không? Tại sao?

a) \(\dfrac{{3ac}}{{{a^3}b}}\) và \(\dfrac{{6c}}{{2{a^2}b}}\)

b) \(\dfrac{{3ab - 3{b^2}}}{{6{b^2}}}\) và \(\dfrac{{a - b}}{{2b}}\) 

Lời giải:

a) Xét hai phân thức 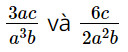 ta có:

3ac.2a²b = 6a³bc;

a³b.6c = 6a³bc.

Do đó 3ac.2a²b = a³b.6c

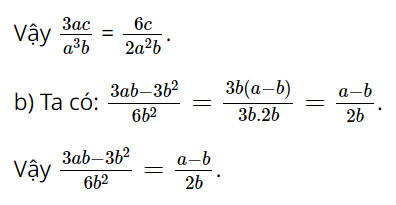
Bài 5 trang 30 SGK Toán 8 Chân trời sáng tạo tập 1

Tìm đa thức thích hợp thay vào ? trong các đẳng thức sau:

Lời giải:

a) Ta có: \(\dfrac{{2x + 1}}{{x - 1}}\) \( = \dfrac{{\left( {2x + 1} \right)\left( {x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = \dfrac{{2{x^2} + 2x + x + 1}}{{{x^2} - 1}} = \dfrac{{{x^2} + 3x + 1}}{{{x^2} - 1}}\)

Vậy đa thức cần tìm là \({x^2} + 3x + 1\)

b) Ta có: \(\dfrac{{{x^2} + 2x}}{{{x^3} + 8}} = \dfrac{{x.\left( {x + 2} \right)}}{{\left( {x + 2} \right)\left( {{x^2} - 2x + 4} \right)}} = \dfrac{x}{{{x^2} - 2x + 4}}\)

Vậy đa thức cần tìm là \(x\)

Bài 6 trang 30 SGK Toán 8 Chân trời sáng tạo tập 1

Rút gọn các phân thức sau:

a) \(\dfrac{{3{x^2}y}}{{2x{y^5}}}\)

b) \(\dfrac{{3{x^2} - 3x}}{{x - 1}}\) 

c) \(\dfrac{{a{b^2} - {a^2}b}}{{2{a^2} + a}}\)

d) \(\dfrac{{12\left( {{x^4} - 1} \right)}}{{18\left( {{x^2} - 1} \right)}}\)

Lời giải:

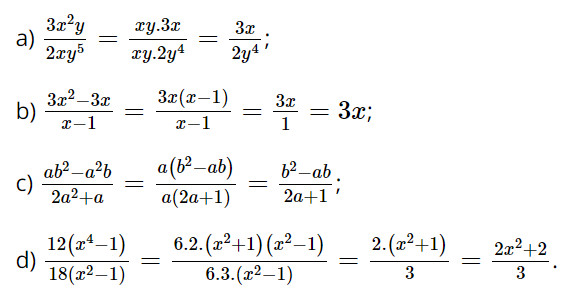
Giaibaitap.me