Bài 1 trang 22 SGK Toán 8 Chân trời sáng tạo tập 1

Tính:

a) \({\left( {3x + 4} \right)^2}\)                                 

b) \({\left( {5x - y} \right)^2}\)                                  

c) \({\left( {xy - \dfrac{1}{2}y} \right)^2}\)

Lời giải:

a) \({\left( {3x + 4} \right)^2} = {\left( {3x} \right)^2} + 2.3x.4 + {4^2} = 9{x^2} + 24x + 16\)

b) \({\left( {5x - y} \right)^2} = {\left( {5x} \right)^2} - 2.5x.y + {y^2} = 25{x^2} - 10xy + {y^2}\)

c) \({\left( {xy - \dfrac{1}{2}y} \right)^2} = {\left( {xy} \right)^2} - 2.xy.\dfrac{1}{2}y + {\left( {\dfrac{1}{2}y} \right)^2} = {x^2}{y^2} - x{y^2} + \dfrac{1}{4}{y^2}\)

Bài 2 trang 22 SGK Toán 8 Chân trời sáng tạo tập 1

Viết các biểu thức sau thành bình phương của một tổng hoặc một hiệu:

a) \({x^2} + 2x + 1\)              

b) \(9 - 24x + 16{x^2}\)                     

c) \(4{x^2} + \dfrac{1}{4} + 2x\)

Lời giải:

a) x² + 2x + 1

= x² + 2.x.1 + 1²

= (x + 1)².

b) 9 – 24x + 16x²

= 3² – 2.3.4x + (4x)²

= (3 – 4x)².

Ta cũng có thể viết như sau:

9 – 24x + 16x²

= 16x² – 24x + 9

= (4x)² – 2.4x.3 + 3²

= (4x – 3)².

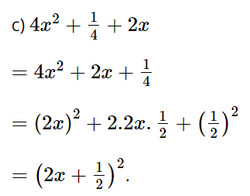
Bài 3 trang 22 SGK Toán 8 Chân trời sáng tạo tập 1

Viết các biểu thức sau thành đa thức:

a) \(\left( {3x - 5} \right)\left( {3x + 5} \right)\)                               

b) \(\left( {x - 2y} \right)\left( {x + 2y} \right)\)                      

c) \(\left( { - x - \dfrac{1}{2}y} \right)\left( { - x + \dfrac{1}{2}y} \right)\)

Lời giải: 

a) \(\left( {3x - 5} \right)\left( {3x + 5} \right) = {\left( {3x} \right)^2} - {5^2} = 9{x^2} - 25\)

b) \(\left( {x - 2y} \right)\left( {x + 2y} \right) = {x^2} - {\left( {2y} \right)^2} = {x^2} - 4{y^2}\)

c) \(\left( { - x - \dfrac{1}{2}y} \right)\left( { - x + \dfrac{1}{2}y} \right) = {\left( { - x} \right)^2} - {\left( {\dfrac{1}{2}y} \right)^2} = {x^2} - \dfrac{1}{4}{y^2}\)

Bài 4 trang 22 SGK Toán 8 Chân trời sáng tạo tập 1

a) Viết biểu thức tính diện tích của hình vuông có cạnh bằng \(2x + 3\) dưới dạng đa thức

b) Viết biểu thức tính thể tích của khối lập phương có cạnh bằng \(3x - 2\) dưới dạng đa thức.

Lời giải: 

a) Biểu thức tính diện tích của hình vuông có cạnh bằng 2x + 3 là:

(2x + 3)² = (2x)² + 2.2x.3 + 3² = 4x² + 12x + 9.

b) Biểu thức tính thể tích của khối lập phương có cạnh bằng 3x − 2 là:

(3x – 2)³ = (3x)³ – 3.(3x)².2 + 3.3x.2² – 2³

               = 27x³ – 54x² + 36x – 8.

Bài 5 trang 22 SGK Toán 8 Chân trời sáng tạo tập 1

Tính nhanh:

a) \(38.42\)                               b) \({102^2}\)                          c) \({198^2}\)              d) \({75^2} - {25^2}\)

Lời giải:

a) \(38.42 = \left( {40 - 2} \right).\left( {40 + 2} \right) = {40^2} - {2^2} = 1600 - 4 = 1596\)

b) \({102^2} = {\left( {100 + 2} \right)^2} = {100^2} + 2.100.2 + {2^2} = 10000 + 400 + 4 = 10404\)

c) \({198^2} = {\left( {200 - 2} \right)^2} = {200^2} - 2.200.2 + {2^2} = 40000 - 800 + 4 = 39204\)

d) \({75^2} - {25^2} = \left( {75 + 25} \right)\left( {75 - 25} \right) = 100.50 = 5000\)

Bài 6 trang 22 SGK Toán 8 Chân trời sáng tạo tập 1

Viết các biểu thức sau thành đa thức:

a) \({\left( {2x - 3} \right)^3}\)                                  

b) \({\left( {a + 3b} \right)^3}\)                                 

c) \({\left( {xy - 1} \right)^3}\)

Lời giải:

a) (2x – 3)³

= (2x)³ – 3.(2x)².3 + 3.2x.3² – 3³

= 8x³ – 36x² + 54x – 8.

b) (a + 3b)³

= a³ + 3.a².3b + 3.a.(3b)² + (3b)³

= a³ + 9a²b + 27ab² + 27b³.

c) (xy –1)³

= (xy)³ – 3.(xy)².1 + 3.xy.1² – 1³

= x³y³ – 3x²y² + 3xy – 1.

Bài 7 trang 22 SGK Toán 8 Chân trời sáng tạo tập 1

Viết các biểu thức sau thành đa thức:

a) \(\left( {a - 5} \right)\left( {{a^2} + 5a + 25} \right)\)                 

b) \(\left( {x + 2y} \right)\left( {{x^2} - 2xy + 4{y^2}} \right)\)

Lời giải:

a) \(\left( {a - 5} \right)\left( {{a^2} + 5a + 25} \right) = \left( {a - 5} \right)\left( {{a^2} + 5a + {5^2}} \right) = {a^3} - {5^3} = {a^3} - 125\)

b) \(\left( {x + 2y} \right)\left( {{x^2} - 2xy + 4{y^2}} \right) = \left( {x + 2y} \right)\left[ {{x^2} - 2.xy + {{\left( {2y} \right)}^2}} \right] = {x^3} + {\left( {2y} \right)^3} = {x^3} + 8{y^3}\)

Bài 8 trang 22 SGK Toán 8 Chân trời sáng tạo tập 1

Viết các biểu thức sau thành đa thức:

a) \(\left( {a - 1} \right)\left( {a + 1} \right)\left( {{a^2} + 1} \right)\)                    b) \({\left( {xy + 1} \right)^2} - {\left( {xy - 1} \right)^2}\)

Lời giải:

a) (a – 1)(a + 1)(a² + 1)

= (a² – 1)(a² + 1)

= (a²)² – 1²

= a⁴ – 1.

b) (xy + 1)² – (xy – 1)²

= [(xy + 1) + (xy – 1)].[(xy + 1) – (xy – 1)]

= [xy + 1 + xy – 1].[xy + 1 – xy + 1]

= 2xy.2

= 4xy.

Bài 9 trang 22 SGK Toán 8 Chân trời sáng tạo tập 1

a) Cho \(x + y = 12\) và \(xy = 35\). Tính \({\left( {x - y} \right)^2}\)

b) Cho \(x - y = 8\) và \(xy = 20\). Tính \({\left( {x + y} \right)^2}\)

c) Cho \(x + y = 5\) và \(xy = 6\). Tính \({x^3} + {y^3}\)

d) Cho \(x - y = 3\) và \(xy = 40\). Tính \({x^3} - {y^3}\)

Lời giải:

a) Ta có: \({\left( {x - y} \right)^2} = {x^2} - 2xy + {y^2} = {x^2} + {y^2} - 2xy = {\left( {x + y} \right)^2} - 4xy\)

Thay \(x + y = 12\) và \(xy = 35\) vào biểu thức trên ta có:

\({12^2} - 4.35 = 144 - 140 = 4\)

Vậy \({\left( {x - y} \right)^2} = 4\) khi \(x + y = 12\), \(xy = 35\)

b) Ta có: \({\left( {x + y} \right)^2} = {x^2} + 2xy + {y^2} = {x^2} + {y^2} + 2xy = {\left( {x - y} \right)^2} + 4xy\)

Thay \(x - y = 8\); \(xy = 20\) vào biểu thức ta có:

\({8^2} + 4.20 = 64 + 80 = 144\)

Vậy \({\left( {x + y} \right)^2} = 44\) khi \(x - y = 8\); \(xy = 20\)

c) Ta có: \({x^3} + {y^3} = {\left( {x + y} \right)^3} - 3{x^2}y - 3x{y^2} = {\left( {x + y} \right)^3} - 3xy\left( {x + y} \right)\)

Thay \(x + y = 5\); \(xy = 6\) vào biểu thức ta có:

\({5^3} - 3.6.5 = 125 - 90 = 35\)

Vậy \({x^3} + {y^3} = 35\) khi \(x + y = 5\); \(xy = 6\)

d) Ta có: \({x^3} - {y^3} = {\left( {x - y} \right)^3} + 3{x^2}y - 3x{y^2} = {\left( {x - y} \right)^3} + 3xy\left( {x - y} \right)\)

Thay \(x - y = 3\); \(xy = 40\) vào biểu thức ta có:

\({3^3} + 3.40.3 = 27 + 360 = 387\)

Vậy \({x^3} - {y^3} = 387\) khi \(x - y = 3\); \(xy = 40\)

Bài 10 trang 22 SGK Toán 8 Chân trời sáng tạo tập 1

Cho hình hộp chữ nhật có chiều dài, chiều rộng, chiều cao đều bằng \(5\)cm. Thể tích của hình hộp chữ nhật sẽ tăng bao nhiêu nếu:

a) Chiều dài và chiều rộng tăng thêm \(a\) cm?

b) Chiều dài, chiều rộng, chiều cao đều tăng thêm \(a\) cm?

Lời giải:

Thể tích hình hộp chữ nhật có chiều dài, chiều rộng, chiều cao đều bằng 5 cm là: 5³ = 125 (cm³).

a) Chiều dài của hình hộp chữ nhật sau khi tăng thêm a cm là: 5 + a (cm).

Chiều rộng của hình hộp chữ nhật sau khi tăng thêm a cm là: 5 + a (cm).

Thể tích hình hộp chữ nhật lúc sau là:

(5 + a).(5 + a).5 = (5 + a)².5

                          = (5² + 2.5.a + a²).5

                          = (25 + 10a + a²).5

                          = 25.5 + 10a.5 + a².5

                          = 125 + 50a + 5a² (cm³).

Khi đó thể tích của hình hộp chữ nhật đã tăng thêm là:

125 + 50a + 5a² – 125 = 5a² + 50a (cm³).

Vậy nếu chiều dài và chiều rộng tăng thêm a cm thì thể tích của hình hộp chữ nhật đã tăng thêm 5a² + 50a (cm³).

b) Chiều cao của hình hộp chữ nhật sau khi tăng thêm a cm là: 5 + a (cm).

Thể tích hình hộp chữ nhật lúc sau là:

(5 + a).(5 + a).(5 + a) = (5 + a)³

                                   = 5³ + 3.5².a + 3.5.a² + a³

                                   = 125 + 75a + 15a² + a³ (cm³).

Khi đó thể tích của hình hộp chữ nhật đã tăng thêm là:

125 + 75a + 15a² + a³ – 125 = a³ + 15a² + 75a (cm³).

Vậy nếu chiều dài, chiều rộng, chiều cao đều tăng thêm a cm thì thể tích của hình hộp chữ nhật đã tăng thêm a³ + 15a² + 75a (cm³).

Giaibaitap.me