Bài 28 trang 103 SGK Hình học 12 Nâng cao

Xác định vị trí tương đối giữa các cặp đường thẳng d và d’ cho bởi phương trình:

a) $d:{{x - 1} \over 2} = y - 7 = {{z - 3} \over 4}\,;\,d':{{x - 3} \over 6} = {{y + 1} \over { - 2}} = {{z + 2} \over 1}$
b)

$d:\left\{ \matrix{ x = t \hfill \cr  y = - 3 - 4t \hfill \cr  z = - 3 - 3t \hfill \cr} \right.$

d’ là giao tuyến của hai mặt phẳng $\left( \alpha  \right):x + y - z = 0,\,\,\left( {\alpha '} \right):2x - y + 2z = 0$.

Giải

a) Đường thẳng d đi qua M(1; 7; 3) và có vectơ chỉ phương $\overrightarrow u  = \left( {2;1;4} \right)$. Đường thẳng d’ đi qua $M'\left( {3; - 1; - 2} \right)$ và có vectơ chỉ phương $\overrightarrow u ' = \left( {6; - 2;1} \right)$.
Ta có $\overrightarrow {MM'}  = \left( {2; - 8; - 5} \right)$ và $\left[ {\overrightarrow u ;\overrightarrow u '} \right] = \left( {9;22; - 10} \right)$

$\Rightarrow \left[ {\overrightarrow u ;\overrightarrow u '} \right].\overrightarrow {MM'}  =  - 108 \ne 0$.
Vậy d và d’ chéo nhau.
b) Đường thẳng d đi qua $M\left( {0; - 3; - 3} \right)$ và có vectơ chỉ phương $\overrightarrow u  = \left( {1; - 4; - 3} \right)$
Đường thẳng d’ có vectơ chỉ phương

d và d’ có cùng vectơ chỉ phương và $M\left( {0; - 3; - 3} \right)$ không nằm trên d’ nên d và d’ song song.

Bài 29 trang 103 SGK Hình học 12 Nâng cao

Viết phương trình đường thẳng đi qua $A\left( {1; - 1;1} \right)$ và cắt cả hai đường thẳng sau:

$d:\left\{ \matrix{ x = 1 + 2t \hfill \cr  y = t \hfill \cr  z = 3 - t \hfill \cr} \right.\,\,;\,\,d':\left\{ \matrix{ x = t \hfill \cr  y = - 1 - 2t \hfill \cr  z = 2 + t \hfill \cr} \right.$

Giải

Lấy điểm $M\left( {1 + 2t,t,3 - 1} \right)$ nằm trên d và điểm $M'\left( {t', - 1 - 2t',2 + t'} \right)$ nằm trên d’.
Rõ ràng $A \notin d$ và $A \notin d'$. Ta tìm t và t’ sao cho A, M, M’ thẳng hàng, tức $\overrightarrow {AM}$ và $\overrightarrow {AM'}$ cùng phương.
Ta có $\overrightarrow {AM}  = \left( {2t,1 + t,2 - t} \right);$

$\overrightarrow {AM'}  = \left( { - 1 + t', - 2t',1 + t'} \right)$. Do đó:

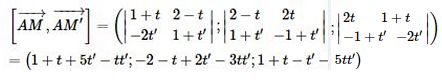
Hai vectơ $\overrightarrow {AM}$ và $\overrightarrow {AM'}$ cùng phương khi và chỉ khi $\left[ {\overrightarrow {AM} ,\overrightarrow {AM'} } \right] = \overrightarrow 0$ hay: 

$\left\{ \matrix{ 1 + t + 5t' - tt' = 0 \hfill \cr  - 2 - t + 2t' - 3tt' = 0 \hfill \cr  1 + t - t' - 5tt' = 0 \hfill \cr} \right.$

Khử số hạng tt’ từ các phương trình trên, ta được hệ

$\left\{ \matrix{ 5 + 4t + 13t' = 0 \hfill \cr  4 + 4t + 26t' = 0 \hfill \cr} \right.$.

Suy ra $t =  - {3 \over 2};t' = {1 \over {13}}$. Khi đó $\overrightarrow {AM}  = \left( { - 3; - {1 \over 2};{7 \over 2}} \right)$.
Gọi $\Delta$ là đường thẳng đi qua A và M, $\Delta$ có vectơ chỉ phương $\overrightarrow u  = 2\overrightarrow {AM}  = \left( { - 6; - 1;7} \right)$ nên có phương trình tham số là: 

$\left\{ \matrix{ x = 1 - 6t \hfill \cr  y = - 1 - t \hfill \cr  z = 1 + 7t \hfill \cr} \right.$

Bài 30 trang 103 SGK Hình học 12 Nâng cao

Viết phương trình đường thẳng song song với đường thẳng ${d_1}$ và cắt cả hai đường thẳng ${d_2}$ và ${d_3}$, biết phương trình của ${d_1},{d_2}$ và ${d_3}$ là:

${d_1}:\left\{ \matrix{ x = 1 \hfill \cr  y = {- 2 + 4t} \hfill \cr  z ={ 1 - t} \hfill \cr} \right.$
${d_2}:{{x - 1} \over 1} = {{y + 2} \over 4} = {{z - 2} \over 3}$
${d_3}:\left\{ \matrix{ x ={ - 4 + 5t'} \hfill \cr  y = {- 7 + 9t'} \hfill \cr  z = {t'} \hfill \cr} \right.$

Giải

Đường thẳng ${d_1}$ có vectơ chỉ phương ${\overrightarrow u _1} = \left( {0;4; - 1} \right)$, ${d_2}$ có phương trình tham số là

$\left\{ \matrix{ x = 1 + t \hfill \cr  y = - 2 + 4t \hfill \cr  z = 2 + 3t \hfill \cr} \right.$

Lấy điểm ${M_2}\left( {1 + t; - 2 + 4t;2 + 3t} \right)$ trên ${d_2}$ và ${M_3}\left( { - 4 + 5t'; - 7 + 9t';t'} \right)$ trên ${d_3}$. Ta tìm t và t’ để $\overrightarrow {{M_2}{M_3}}$ cùng phương với $\overrightarrow {{u_1}}$.
Ta có $\overrightarrow {{M_2}{M_3}}  = \left( { - 5 + 5t' - t; - 5 + 9t' - 4t; - 2 + t' - 3t} \right)$, $\overrightarrow {{M_2}{M_3}}$ cùng phương với $\overrightarrow {{u_1}}$ khi và chỉ khi

$\left\{ \matrix{ - 5 + 5t' - t = 0 \hfill \cr  {{ - 5 + 9t' - 4t} \over 4} = {{ - 2 + t' - 3t} \over { - 1}} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ t = 0 \hfill \cr  t' = 1 \hfill \cr} \right.$

Khi đó ${M_2}\left( {1; - 2;2} \right)$ và $\overrightarrow {{M_2}{M_3}}  = \left( {0;4; - 1} \right)$.
Vậy $\Delta$ qua ${M_2},{M_3}$ có phương trình:

$\left\{ \matrix{ x = 1 \hfill \cr  y = - 2 + 4t \hfill \cr  z = 2 - t \hfill \cr} \right.$.

Rõ ràng ${M_2} \notin {d_1}$. Vậy $\Delta$ chính là đường thẳng cần tìm.

Bài 31 trang 103 SGK Hình học 12 Nâng cao

Cho hai đường thẳng

${d_1}:\left\{ \matrix{ x = 8 + t \hfill \cr  y = 5 + 2t \hfill \cr  z = 8 - t \hfill \cr} \right.$ và ${d_2}:{{3 - x} \over 7} = {{y - 1} \over 2} = {{z - 1} \over 3}$.

a) Chứng tỏ rằng hai đường thẳng đó chéo nhau.
b) Viết phương trình mặt phẳng đi qua gốc tọa độ O và song song với ${d_1}$ và ${d_2}$.
c) Tính khoảng cách giữa hai đường thẳng ${d_1}$ và ${d_2}$.
d) Viết phương trình đường vuông góc chung của hai đường thẳng đó.

Giải

a) Đường thẳng ${d_1}$ đi qua ${M_1}\left( {8;5;8} \right)$ có vectơ chỉ phương $\overrightarrow {{u_1}} \left( {1;2; - 1} \right)$.
Đường thẳng ${d_2}$ đi qua ${M_2}\left( {3;1;1} \right)$ có vectơ chỉ phương $\overrightarrow {{u_2}} \left( { - 7;2;3} \right)$.
Ta có: $\overrightarrow {{M_2}{M_1}}  = \left( {5;4;7} \right)\,\,;\,\,\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right] = \left( {8;4;16} \right)$.
Do đó $\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right].\overrightarrow {{M_2}{M_1}}  = 168 \ne 0$.
Vậy hai đường thẳng ${d_1}$ và ${d_2}$ chéo nhau.
b) Gọi $\left( \alpha  \right)$ là mặt phẳng qua O song song với cả ${d_1}$ và ${d_2}$. $Mp\left( \alpha  \right)$ có vectơ pháp tuyến là $\overrightarrow n  = {1 \over 4}\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right] = \left( {2;1;4} \right)$.
Vậy $\left( \alpha  \right):2\left( {x - 0} \right) + 1\left( {y - 0} \right) + 4\left( {z - 0} \right) = 0$

$\Leftrightarrow 2x + y + 4z = 0$.
Rõ ràng ${M_1},{M_2} \notin \left( \alpha  \right)$. Vậy $\left( \alpha  \right)$ chính là mặt phẳng cần tìm.
c) Khoảng cách giữa hai đường thẳng chéo nhau ${d_1}$ và ${d_2}$ là:

$d = {{\left| {\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right].\overrightarrow {{M_2}{M_1}} } \right|} \over {\left| {\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right]} \right|}} = {{168} \over {\sqrt {{8^2} + {4^2} + {{16}^2}} }} = 2\sqrt {21}$

d) Giả sử PQ là đường vuông góc chung của ${d_1}$ và ${d_2}$ với $P \in {d_1}\,;\,Q \in {d_2}$. Khi đó ta có các giá trị t và t’ sao cho: $P\left( {8 + t\,;5 + 2t\,;\,8 - t} \right),$

$Q\left( {3 - 7t'\,;\,1 + 2t'\,;\,1 + 3t'} \right)$.
Ta có: $\overrightarrow {PQ}  = \left( { - 5 - 7t' - t; - 4 + 2t' - 2t; - 7 + 3t' + t} \right)$.
Vectơ $\overrightarrow {PQ}$ đồng thời vuông góc với hai vectơ chỉ phương $\overrightarrow {{u_1}}$ và $\overrightarrow {{u_2}}$ nên

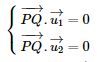
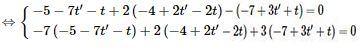
Vậy $P\left( {7;3;9} \right)\,,\,Q\left( {3;1;1} \right)$ và do đó, đường vuông góc chung của ${d_1}$ và ${d_2}$ có phương trình:

${{x - 3} \over {7 - 3}} = {{y - 1} \over {3 - 1}} = {{z - 1} \over {9 - 1}} \Leftrightarrow {{x - 3} \over 2} = {{y - 1} \over 1} = {{z - 1} \over 4}$

Giaibaitap.me