Bài 23 trang 29 SGK Hình học 12 Nâng cao

Cho khối chóp tam giác \(S.ABC\). Trên ba đường thẳng \(SA, SB,SC\) lần lượt lấy ba điểm \(A’, B’, C'\) khác với \(S\). Gọi \(V\) và \(V’\) lần lượt là thể tích của các khối chóp \(S.ABC\) và \(S.A'B'C'\). Chứng minh rằng:

 \({V \over {V'}} = {{SA} \over {SA'}}.{{SB} \over {SB'}}.{{SC} \over {SC'}}\)

Giải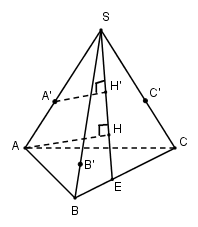

Gọi \(H\) và \(H’\) lần lượt là hình chiếu của \(A\) và \(A’\) trên mp \((SBC)\). Khi đó \(3\) điểm \(S, H, H’\) thẳng hàng (vì chúng là hình chiếu của ba điểm thẳng hàng \(S, A, A’\) trên mp \((SBC)\)) và vì \(A’H’ // AH\) nên \({{AH} \over {A'H'}} = {{SA} \over {SA'}}\). Ta có:
\({{{S_{SBC}}} \over {{S_{SB'C'}}}} = {{{1 \over 2}SB.SC.sin\widehat {BSC}} \over {{1 \over 2}SB'.SC'.sin\widehat {B'SC'}}} = {{SB} \over {SB'}}.{{SC} \over {SC'}}\)
Suy ra \({V \over {V'}} = {{{V_{A.SBC}}} \over {{V_{A'.SB'C'}}}} = {{{1 \over 3}{S_{SBC}}.AH} \over {{1 \over 3}{S_{SB'C'}}.A'H'}} = {{SA} \over {SA'}}.{{SB} \over {SB'}}.{{SC} \over {SC'}}\)

Bài 24 trang 29 SKG Hình học 12 Nâng cao

Khối chóp \(S.ABCD\) có đáy là hình bình hành, \(M\) là trung điểm của cạnh \(SC\). Mặt phẳng \((P)\) đi qua \(AM\), song song với \(BD\) chia khối chóp thành hai phần. Tính tỉ số thể tích cùa hai phần đó.

Giải

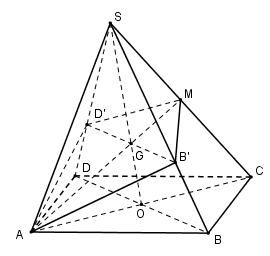
Gọi \(O\) là tâm hình bình hành \(ABCD\). Gọi \(G\) là giao điểm của \(SO\) và \(AM\) thì \(G\) là trọng tâm của tam giác \(SAC\) nên \({{SG} \over {SO}} = {2 \over 3}\).
Mặt phẳng \((P)\) song song với \(BD\) nên \((P)\) cắt mp \((SBD)\) theo giao tuyến \(B’D’\) đi qua \(G\) và \(B’D’ // BD\), trong đó \(B’, D’\) lần lượt trên \(SB\) và \(SD\).
có \(B’D’ // BD\) nên \({{SB'} \over {SB}} = {{SD'} \over {SD}} = {{SG} \over {SO}} = {2 \over 3}\)
Mặt phẳng \((P)\) chia khối chóp \(S.ABCD\) thành hai phần: Khối chóp \(S.AB’MD’\) và khối đa diện \(ABCDB’MD’\).

\({{{V_{S.AB'D'}}} \over {{V_{S.ABD}}}} = {{SA} \over {SA}}.{{SB'} \over {SB}}.{{SD'} \over {SD}} = {2 \over 3}.{2 \over 3} = {4 \over 9} \Rightarrow {{{V_{S.AB'D'}}} \over {{V_{S.ABCD}}}} = {2 \over 9}\)
(Vì \({V_{S.ABCD}} = 2{V_{S.ABD}}\))
\({{{V_{S.MB'D'}}} \over {{V_{S.CBD}}}} = {{SM} \over {SC}}.{{SB'} \over {SB}}.{{SD'} \over {SD}} = {1 \over 2}.{2 \over 3}.{2 \over 3} = {2 \over 9} \)

\(\Rightarrow {{{V_{S.MB'D'}}} \over {{V_{S.ABCD}}}} = {1 \over 9}\)
Từ đó suy ra \({{{V_{S.AB'MD'}}} \over {{V_{S.ABCD}}}} = {{{V_{S.AB'D'}} + {V_{S.MB'D'}}} \over {{V_{S.ABCD}}}} = {2 \over 9} + {1 \over 9} = {1 \over 3}\)
Vậy \({{{V_{S.AB'MD'}}} \over {{V_{ABCDB'MD'}}}} = {1 \over 2}\)

Bài 25 trang 29 SGK Hình học 12 Nâng cao

Chứng minh rằng nếu có phép vị tự tỉ số \(k\) biến tứ diện \(ABCD\) thành tứ diện \(A’B’C’D’\)a thì \({{{V_{A'B'C'D'}}} \over {{V_{ABCD}}}} = {\left| k \right|^3}\)

Giải
Giả sử phép vị tự \(f\) tỉ số \(k\) biến hình chóp \(A.BCD\) thành hình chóp \(A’.B’C’D’\). Khi đó, \(f\) biến đường cao \(AH\) của hình chóp \(A.BCD\) thành đường cao \(A‘H’\) của hình chóp \(A’.B’C’D’\) do đó \(A'H' = \left| k \right|AH\). Tam giác \(BCD\) được biến thành tam giác \(B’C’D’\) qua \(f\) nên \({S_{B'C'D'}} = {k^2}{S_{BCD}}\)
Từ đó suy ra \({{{V_{A'B'C'D'}}} \over {{V_{ABCD}}}} = {{{1 \over 3}{S_{B'C'D'}}.A'H'} \over {{1 \over 3}{S_{BCD}}.AH}} = {\left| k \right|^3}\)

Giaibaitap.me