Bài 17 trang 59 SGK Hình học 12 Nâng cao

Trong mỗi trường hợp sau, hãy gọi tên hình tròn xoay:

a) Sinh bởi ba cạnh của một tam giác cân khi quay quanh trục đối xứng của tam giác đó.

b) Sinh bởi một tam giác vuông (kể cả điểm trong) khi quay quanh đường thẳng chứa một cạnh góc vuông.

Giải

a) Hình nón

b) Khối nón.

Bài 18 trang 59 SGK Hình học 12 Nâng cao

Cho điểm \(A\) nằm trong mặt cầu \(S\). Chứng minh rằng các đường thẳng đi qua \(A\) tiếp xúc với mặt cầu \(S\) luôn nằm trên một mặt nón xác định.

Giải

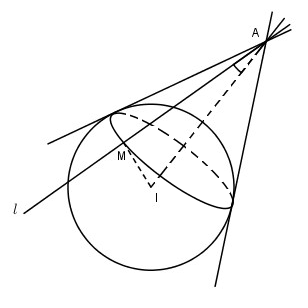
Giả sử \(Al\) là một tiếp tuyến của mặt cầu \(S(I;R)\) với tiếp điểm là \(M\). Khi đó nếu \(\Delta \) là đường thẳng \(AI\) và \(\alpha \) là góc giữa đường thẳng \(Al\) và \(\Delta \) thì \(\alpha  = \widehat {MAI}\).

Ta có: \(9\sin \alpha  = {{MI} \over {IA}} = {R \over {IA}}\), suy ra góc \(\alpha \) không đổi. Vậy \(Al\) là đường sinh của mặt nón \((N)\) có đỉnh \(A\) và góc ở đỉnh là \(2\alpha \).

Bài 19 trang 60 SGK Hình học 12 Nâng cao

Một mặt cầu gọi là ngoại tiếp một hình nón nếu mặt cầu đó đi qua đỉnh của hình nón và đi qua đường tròn đáy của hình nón. Hình nón như vậy gọi là nội tiếp mặt cầu đó.

a) Chứng minh rằng mọi hình nón đều có mặt cầu ngoại tiếp duy nhất.

b) Một hình nón có chiều cao \(h\) và bán kính đáy bằng \(r\). Tìm bán kính mặt cầu ngoại tiếp hình nón đó.

c) Cho hình nón nội tiếp mặt cầu bán kính \(R\). Nếu hình nón đó có chiều cao bằng \(h\) thì bán kính đáy của nó bằng bao nhiêu? Tính diện tích xung quanh của hình nón đó.

Giải

a)

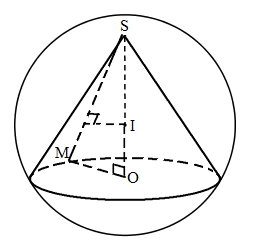
Hình nón \((N)\) có đỉnh \(S\) và đường tròn đáy là \((O;r)\). Lấy điểm \(M\) trên \((O;r)\) thì \(\Delta SOM\) vuông tại \(O\).

\(SO\) là trục của đường tròn \((O;r)\) nên \(I\) là tâm của mặt cầu ngoại tiếp hình nón khi và chỉ khi \(I\) thuộc \(SO\) và cách đều hai điểm \(S, M\). Vậy \(I\) là giao điểm của \(SO\) với mặt phẳng trung trực của \(SM\). Mặt cầu tâm \(I\) bán kính \(R = IS\) là mặt cầu ngoại tiếp duy nhất.

b)

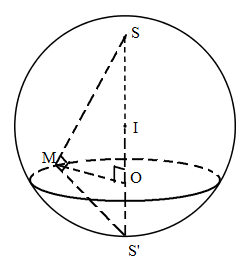
Kẻ đường kính \(SS’\) của mặt cầu ngoại tiếp hình nón \((SS’ > h)\)

\(\Delta MSS'\) vuông tại \(M\) có đường cao \(MO = r\).

Ta có:

\(\eqalign{
& M{O^2} = OS.OS' \Rightarrow {r^2} = h\left( {SS' - h} \right) \cr 
& \Rightarrow SS' = {{{r^2}} \over h} + h = {{{r^2} + {h^2}} \over h} \cr} \)

Vậy bán kính mặt cầu ngoại tiếp hình nón là \(R = {1 \over 2}SS' = {{{r^2} + {h^2}} \over {2h}}\)

c) Nếu hình nón có chiều cao \(h\), bán kính đáy là \(r\) nội tiếp mặt cầu bán kính \(R\) thì theo câu b) ta có hệ thức \({r^2} = h\left( {2R - h} \right)\).

Vậy \(r = \sqrt {h\left( {2R - h} \right)} \)

Độ dài đường sinh \(l = SM = \sqrt {SO.SS'}  = \sqrt {2R.h} \)

Diện tích xung quanh của hình nón là \({S_{xq}} = \pi rl = \pi \sqrt {h\left( {2R - h} \right)} .\sqrt {2Rh} \)

\(= \pi h\sqrt {2R\left( {2R - h} \right)} \)

Giaibaitap.me