Bài 1 trang 63 SGK Hình học 12 Nâng cao

Cho mp  $(P)$ và điểm $A$ không thuộc $(P)$. Chứng minh rằng mọi mặt cầu đi qua $A$ và có tâm nằm trên $(P)$ luôn luôn đi qua hai điểm cố định.

Giải

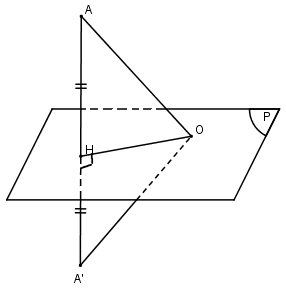
Lấy điểm $O$ nằm trên mp $(P)$. Gọi $(S)$ là mặt cầu đi qua $A$ có tâm $O$.

Gọi $A’$ là điểm đối xứng của $A$ qua mp $(P)$ ta có $OA’ = OA = R$ nên $(S)$ đi qua $A’$. Vậy mặt cầu $(S)$ luôn đi qua hai điểm cố định $A$ và $A’$.

Bài 2 trang 63 SGK Hình học 12 Nâng cao

Xác định tâm và bán kính của mặt cầu ngoại tiếp hình chóp $S.ABC$, biết $SA = SB = SC = a$, $\widehat {ASB} = {60^0},\widehat {BSC} = {90^0},\widehat {CSA} = {120^0}$.

Giải

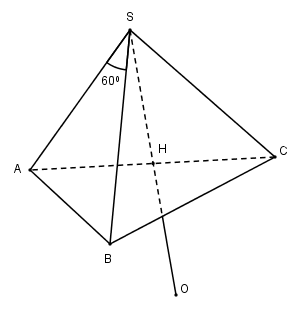
Áp dụng định lí Cosin trong tam giác $SAB, SAC$ ta có:

$\eqalign{ & A{B^2} = S{A^2} + S{B^2} - 2SA.SB.\cos {60^0} \cr  & = {a^2} + {a^2} - 2{a^2}.{1 \over 2} = {a^2} \Rightarrow AB = a \cr  & A{C^2} = S{A^2} + S{C^2} - 2SA.SC.\cos {120^0} \cr  & = {a^2} + {a^2} - 2{a^2}\left( { - {1 \over 2}} \right) = 3{a^2} \Rightarrow AC = a\sqrt 3 \cr}$

Trong tam giác vuông $SBC$ có: $B{C^2} = S{B^2} + S{C^2} = 2{a^2} \Rightarrow BC = a\sqrt 2$

Ta có: $A{C^2} = A{B^2} + B{C^2} \Rightarrow \Delta ABC$ vuông tại $B$.

Gọi $H$ là trung điểm của $AC$ thì $H$ là tâm đường tròn ngoại tiếp tam giác ABC.

Vì $SA = SB = SC$ nên $SH \bot mp\left( {ABC} \right)$

Và $S{H^2} = S{C^2} - H{C^2} = {a^2} - {\left( {{{a\sqrt 3 } \over 2}} \right)^2} = {{{a^2}} \over 4}$

$\Rightarrow SH = {a \over 2}$

Gọi $O$ là điểm đối xứng của $S$ qua $H$ thì $SO = OA = OB = OC = a$ nên mặt cầu ngoại tiếp hình chóp $S.ABC$ có tâm $O$ và bán kính $R = a$.

Bài 3 trang 63 SGK Hình học 12 Nâng cao

Cho hai đường tròn $(O; r)$ và $(O’; r’)$ cắt nhau tại hai điểm $A, B$ và lần lượt nằm trên hai mặt phẳng phân biệt $(P)$ và $(P’)$.

a) Chứng minh rằng có mặt cầu $(S)$ đi qua hai đường tròn đó.

b) Tìm bán kính $R$ của mặt cầu $(S)$ khi $r = 5, r' = \sqrt {10}$, $AB = 6$, ${\rm{OO}}' = \sqrt {21}$.

Giải

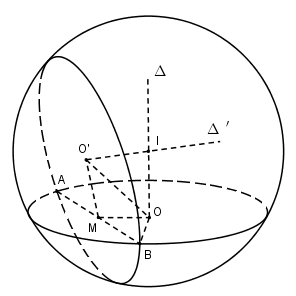
a) Gọi $M$ là trung điểm của $AB$ ta có: $OM \bot AB$ và $O'M \bot AB \Rightarrow AB \bot \left( {OO'M} \right)$

Gọi $\Delta ,\,\Delta '$ lần lượt là trục của đường tròn $(O; r)$ và $(O’; r’)$ thì $AB \bot \Delta \,\,,\,\,AB \bot \Delta '$. Do đó $\Delta ,\,\Delta '$ cùng nằm trong mp $(OO’M)$.

Gọi $I$ là giao điểm của $\Delta$ và $\Delta '$ thì $I$ là tâm của mặt cầu $(S)$ đi qua hai đường tròn $(O; r)$ và $(O’; r’)$ và $S$ có bán kính $R = IA$.

b) Ta có: $MA = MB = 3\,\,,\,\,OA = r = 5,\,\,OA' = r' = \sqrt {10}$

$\eqalign{ & OM = \sqrt {O{A^2} - A{M^2}} = \sqrt {25 - 9} = 4 \cr  & O'M = \sqrt {O'{A^2} - A{M^2}} = \sqrt {10 - 9} = 1 \cr}$

Áp dụng định lí Cosin trong $\Delta {\rm{OMO'}}$ ta có:

$\eqalign{ & OO{'^2} = O{M^2} + O'{M^2} - 2OM.O'M.\cos \widehat {OMO'} \cr  & \Rightarrow 21 = 16 + 1 - 2.4.1.cos\widehat {OMO'} \cr&\Rightarrow \cos \widehat {OMO'} = - {1 \over 2} \cr  & \Rightarrow \widehat {OMO'} = {120^0},\,\,\widehat {OIO'} = {60^0} \cr}$

Áp dụng định lí Côsin trong tam giác $OMO’$ ta có:

$\eqalign{ & M{O^2} = MO{'^2} + OO{'^2} - 2MO'.OO'.cos\widehat {MO'O} \cr  & \Rightarrow \cos \widehat {MO'O} = {{\sqrt {21} } \over 7} \Rightarrow \sin \widehat {OO'I} = {{\sqrt {21} } \over 7} \cr}$

(Vì $\widehat {MO'O} + \widehat {OO'I} = {90^0}$)

Áp dụng định lí Cosin trong tam giác $OIO’$ ta có: 
${{OI} \over {\sin \widehat {OO'I}}} = {{OO'} \over {\sin \widehat {OIO'}}} \Leftrightarrow {{OI} \over {{{\sqrt {21} } \over 7}}} = {{\sqrt {21} } \over {{{\sqrt 3 } \over 2}}} \Leftrightarrow OI = 2\sqrt 3$

Vậy $R = \sqrt {O{A^2} + O{I^2}}  = \sqrt {25  + 12} = \sqrt {37}$

Giaibaitap.me