Bài 1 trang 77 sgk giải tích 12

Vẽ đồ thị của các hàm số:

a) \(y = 4^x\);

b) \(y= \left ( \frac{1}{4} \right )^{x}\).

Giải

a) Đồ thị hàm số \(y = 4^x\) 

Tập xác định: \(\mathbb R\)

Sự biến thiên:

\(y' = {4^x}\ln 4 > 0,\forall x \in \mathbb R\)

- Hàm số đồng biến trên \(\mathbb R\)

- Giới hạn đặc biệt:

   \(\eqalign{
& \mathop {\lim }\limits_{x \to - \infty } y = 0 \cr 
& \mathop {\lim }\limits_{x \to + \infty } y = + \infty \cr} \)

Tiệm cận ngang: \(y=0\)

- Bảng biến thiên:

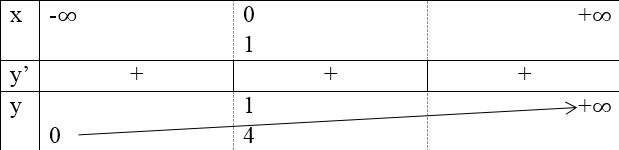
Đồ thị:

Đồ thị nằm hoàn toàn phía trên trục hoành, cắt trục tung tại các điểm \((0;1)\), đi qua điểm \((1;4)\) và qua các điểm \((\frac{1}{2}; 2)\), \((-\frac{1}{2}; \frac{1}{2})\), \((-1; \frac{1}{4})\).

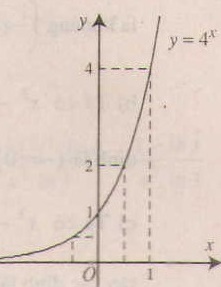
b) Đồ thị hàm số \(y=\left ( \frac{1}{4} \right )^{x}\) 

Tập xác định: \(\mathbb R\)

Sự biến thiên:

\(y' =  - {\left( {{1 \over 4}} \right)^x}\ln 4 < 0,\forall x \in \mathbb R\)

- Hàm số nghịch biến trên \(\mathbb R\)

- Giới hạn:

  \(\eqalign{
& \mathop {\lim }\limits_{x \to - \infty } y = + \infty \cr 
& \mathop {\lim }\limits_{x \to + \infty } y = 0 \cr} \)

Tiệm cận ngang \(y=0\)

- Bảng biến thiên:

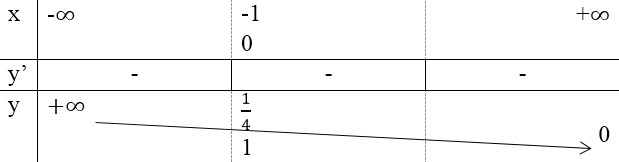
Đồ thị:

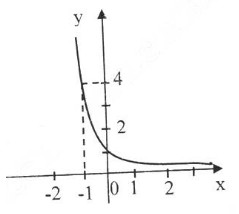
Đồ thị hàm số nằm hoàn toàn về phía trên trục hoành, cắt trục tung tại điểm (0; 1), đi qua điểm (1; \(\frac{1}{4}\)) và qua các điểm (\(-\frac{1}{2}\); 2), (-1;4). 

Bài 2 trang 77 sgk giải tích 12

Tính đạo hàm của các hàm số:

a) \(y = 2xe^x +3sin2x\);

b) \(y = 5x^2- 2^xcosx\);

c) \(y = {{x + 1} \over {{3^x}}}\).

Giải:

a) \(y' = (2x{e^x})' + 3(\sin 2x)' = 2.{e^x} + 2x({e^x})'\)

\(+ {\rm{ }}3.2cos2x\)=\(2\left( {1 + x} \right){e^x} + 6cos2x\)

b) \(y' = 10x-({2^x}cosx)'\)\( = 10x-({2^x}ln2.cosx-{2^x}.sinx)\)\(= 10x - {2^x}\left( {ln2.cosx-sinx} \right)\).

c) 

\(\eqalign{
& y' = \left( {x + 1} \right)'. {3^{ - x}} + \left( {x + 1} \right)\left( {{3^{ - x}}} \right)' \cr 
& = {3^{ - x}} + \left( {x + 1} \right){3^{ - x}}\ln 3,\left( { - x} \right)' \cr 
& = {3^{ - x}}\left[ {1 - \ln 3\left( {x + 1} \right)} \right] \cr 
& = {{1 - \left( {{\rm{x}} + 1} \right)\ln 3} \over {{3^x}}} \cr} \)

Bài 3 trang 77 sgk giải tích 12

Tìm tập xác định của các hàm số:

a) \(y = lo{g_2}\left( {5 - 2x} \right)\) ;

b) \(y =lo{g_3}({x^2} - 2x)\) ;

c) \(y=log_{\frac{1}{5}}\left ( x^{2} -4x+3 \right )\);

d) \(y= log_{0,4}\frac{3x+1}{1-x}\).

Giải:

Hàm số \(y = log_{a}\varphi (x)\) ( cơ số a dương, khác 1 đã cho) xác định khi và chỉ khi \(\varphi (x)\) > 0. Vì vậy hàm số \(y= log_{a}\varphi (x)\) có tập xác định là tập nghiệm bất phương trình \(\varphi (x)\) > 0.

a) ta có \(5- 2x > 0\) \(\Leftrightarrow x < \frac{5}{2}\). Vậy hàm số \(y = lo{g_2}\left( {5 - 2x} \right)\) có tập xác định là khoảng \(\left( { - \infty ;{5 \over 2}} \right)\).

b) Ta có \(x^2-2x > 0 \Leftrightarrow x< 0\) hoặc \(x>2\) . Vậy hàm số \(y =lo{g_3}({x^2} - 2x)\) có tập xác định là khoảng \((-∞; 0) ∪ (2;+∞)\).

c) Ta có \( x^2- 4x + 3 > 0 \Leftrightarrow x< 1\) hoặc \(x> 3\). vậy hàm số \(y= log_{\frac{1}{5}}\left ( x^{2} -4x+3 \right )\) có tập xác định là \((-∞; 1) ∪ (3;+∞)\).

d) Ta có \(\frac{3x+2}{1-x} > 0\) \(\Leftrightarrow (3x+2) (1-x) > 0\) \(\Leftrightarrow\) \(-\frac{2}{3} < x <1\).

Vậy hàm số \(y = log_{0,4}\frac{3x+1}{1-x}\) có tập xác định là khoảng \(\left( { - {2 \over 3};1} \right)\).

Giaibaitap.me