Bài 5 trang 50 SGK Hình học 12

Cho tứ diện đều \(ABCD\) cạnh \(a\). Gọi \(H\) là hình chiếu vuông góc của đỉnh \(A\) xuống mặt phẳng \((BCD)\).

a) Chứng minh \(H\) là tâm đường tròn ngoại tiếp tam giác \(BCD\). Tính độ dài đoạn \(AH\).

b) Tính diện tích xung quanh và thể tích của khối trụ có đường tròn đáy ngoại tiếp tam giác \(BCD\) và chiều cao \(AH\).

Giải

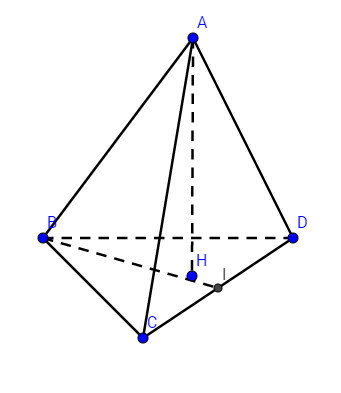
a) Ta biết rằng tứ diện đều là tứ diện có \(6\) cạnh đều bằng nhau.

Vì \(AB = AC = AD\) và \(AH \bot (BCD)\) nên có \(HB = HC = HD\).

Vậy \(H\) là tâm đường tròn ngoại tiếp tam giác đều \(BCD\).

Ta có \(BH = {2 \over 3}BI = {{a\sqrt 3 } \over 3}\);

Do tam giác \(ABH\) vuông tại \(H\) nên : \(A{H^2} = A{B^2} - B{H^2}={a^2} - {{{a^2}} \over 3} = {2 \over 3}{a^2}\) .

Vậy \(AH = {{\sqrt 6 } \over 3}a\)

b) Vì tam giác \(BCD\) đều cạnh \(a\), nên bán kính đường tròn ngoại tiếp tam giác là \(R = BH = {{a\sqrt 3 } \over 3}\) . Vì vậy diện tích xung quanh của hình trụ là:

\(S = 2\pi Rh = 2\pi {{a\sqrt 3 } \over 3}.{{\sqrt 6 } \over 3}a = {{2\sqrt 2 } \over 3}\pi {a^2}\) (đtdt).

Thể tích khối trụ là: \(V = \pi {R^2}h = \pi {{{a^2}} \over 3}.{{\sqrt 6 } \over 3}a = {{\sqrt 6 } \over 9}\pi {a^3}\) (đtdt)

Bài 6 trang 50 SGK Hình học 12

Cho hình vuông \(ABCD\) cạnh \(a\). Từ tâm \(O\) của hình vuông dựng đường thẳng \(\Delta\) vuông góc với mặt phẳng \((ABCD)\). Trên \(\Delta\) lấy điểm \(S\) sao cho \(OS ={a \over 2}\). Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp \(S.ABCD\). Tính diện tích của mặt cầu và thể tích của khối cầu được tạo nên bởi mặt cầu đó.

Giải

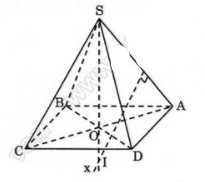
Do \(\Delta\) là trục của hình vuông \(ABCD\), nên tâm \(I\) của mặt cầu ngoại tiếp hình chóp \(S.ABCD\) nằm trên \(\Delta\).

Vì \(SO = {a \over 2} < OC = {{a\sqrt 2 } \over 2}\) nên tâm \(I\) của mặt cầu nằm trên phần kéo dài của \(SO\).

Ta có: \(SI = IC \Rightarrow {a \over 2} + OI = \sqrt {O{I^2} + O{C^2}} \)

\( \Rightarrow {\left( {{a \over 2} + OI} \right)^2} = O{I^2} + {{{a^2}} \over 2}\)

\( \Rightarrow O{I^2} + a.OI + {{{a^2}} \over 4} = O{I^2} + {{{a^2}} \over 4}\)

\( \Rightarrow OI = {a \over 4} \Rightarrow R = SO + OI = {{3a} \over 4}\)

Vậy tâm \(I\) của mặt cầu ngoại tiếp hình chóp \(S.ABCD\) nằm trên \(SO\) mà \(SI = R =\) \({{3a} \over 4}\) ; (\(R\) là bán kính hình cầu). Khi đó diện tích mặt cầu là:

\(S = 4\pi {R^2} = {9 \over 4}\pi {a^2}\) (đvdt)

Thể tích của khối cầu là: \(V = {4 \over 3}\pi {R^3} = {9 \over {16}}{\pi ^3}\) (đvdt)

Bài 7 trang 50 SGK Hình học 12

Cho hình trụ có bán kính đáy \(r\), trục \(OO' = 2r\) và mặt cầu đường kính \(OO'\).

a) Hãy so sánh diện tích mặt cầu và diện tích xung quanh của hình trụ đó.

b) Hãy so sánh thể tích khối trụ và thể tích khối cầu được tạo nên bởi hình trụ và mặt cầu đã cho.

Giải

a) \(S\)_{mặt cầu} = \(4πr^2\)

\(S\)_{hình trụ} = \(4πr^2\)                       

Vậy \(S\)_{mặt cầu}=\(S\)_{hình trụ}

b) \(V\)_{khối cầu} = \({4 \over 3}\pi {r^3}\)

\(V\)_{khối trụ} = \(2πr^3\)                         

Vậy \({{{V_{KT}}} \over {{V_{KC}}}} = {{2\pi {r^3}} \over {{4 \over 3}\pi {r^3}}} = {3 \over 2}\).

Giaibaitap.me