Bài 8 trang 91 - SGK Hình học 12

Cho điểm \(M(1 ; 4 ; 2)\) và mặt phẳng \((α): x + y + z -1 = 0\).

a) Tìm tọa độ điểm \(H\) là hình chiếu vuông góc của điểm \(M\) trên mặt phẳng \((α)\) ;

b) Tìm tọa độ điểm \(M'\) đối xứng với \(M\) qua mặt phẳng \((α)\).

c) Tính khoảng cách từ điểm \(M\) đến mặt phẳng \((α)\).

Giải:

a) Xét đường thẳng \(d\) qua \(M\) và \(d ⊥ (α)\).

Khi đó \(H\) chính là giao điểm của \(d\) và \((α)\). 

Vectơ \(\overrightarrow{n}(1 ; 1 ; 1)\) là vectơ pháp tuyến của \((α)\) nên \(\overrightarrow{n}\) là vectơ chỉ phương của \(d\).

Phương trình tham số của đường thẳng \(d\) có dạng:    \(\left\{\begin{matrix} x=1+t & \\ y=4+t & \\ z=2+t & \end{matrix}\right.\).

Thay tọa độ \(x ; y ; z\) của phương trình trên vào phương trình xác định \((α)\), ta có:

\(3t + 6 = 0 => t = -2 => H(-1 ; 2 ; 0)\).

b) Gọi \(M'(x ; y ; z)\) là điểm đối xứng của \(M\) qua mặt phẳng \((α)\), thì hình chiếu vuông góc \(H\) của \(M\) xuống \((α)\) chính là trung điểm của \(MM'\).

Ta có: 

\(\frac{x+1}{2}=-1 => x = -3\) ;

\(\frac{y+4}{2}=2   => y = 0\) ;

\(\frac{z+2}{2}=0    => z = -2\).

Vậy \(M'(-3 ; 0 ;2)\).

c) Tính khoảng cách từ điểm \(M\) đến mặt phẳng \((α)\) 

Cách 1: \(d(M,(\alpha ))=\frac{|1+4+2-1|}{\sqrt{1+1+1}}=\frac{6}{\sqrt{3}}=2\sqrt{3}\).

Cách 2: Khoảng cách từ M đến (α) chính là khoảng cách MH:

     \(d(M,(α) )= MH\) = \(\sqrt{2^{2}+2^{2}+2^{2}}=2\sqrt{3}\).

Bài 9 trang 91 - SGK Hình học 12

Cho hai đường thẳng:

\(d\): \(\left\{\begin{matrix} x=1-t & \\ y=2+2t & \\ z=3t& \end{matrix}\right.\) và \(d'\): \(\left\{\begin{matrix} x=1+t' & \\ y=3-2t' & \\ z=1& \end{matrix}\right.\).

Chứng minh d và d' chéo nhau.

Giải:

Đường thẳng \(d\) qua điểm \(M(1 ; 2 ; 0)\) và có vec tơ chỉ phương \(\overrightarrow{u}(-1 ; 2 ; 3)\).

Đường thẳng \(d'\) qua điểm \(M'(1 ; 3 ;1)\) và có vectơ chỉ phương \(\overrightarrow{u'}(1 ; -2 ; 0)\).

Cách 1. Xét \(\left [\overrightarrow{u},\overrightarrow{u'} \right ]=\left (\begin{vmatrix} 2 & 3\\ -2&0 \end{vmatrix};\begin{vmatrix} 3 &-1 \\ 0&1 \end{vmatrix};\begin{vmatrix} -1 & 2\\ 1& -2 \end{vmatrix} \right )\)

                                    \(= (6 ; 3 ;0)\).

                     \(\overrightarrow{MM'} = (0 ; 1 ; 1)\).

Ta có : \(\left [\overrightarrow{u},\overrightarrow{u'} \right ].\overrightarrow{MM'}= 6.0 + 3.1 + 0.1 = 3≠ 0\).

Do đó d và d' chéo nhau.

Bài 10 trang 91 - SGK Hình học 12.

Giải bài toán sau đây bằng phương pháp tọa độ:

Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(1\). Tính khoảng cách từ đỉnh \(A\) đến các mặt phẳng \((A'BD)\) và \((B'D'C)\).

 Giải

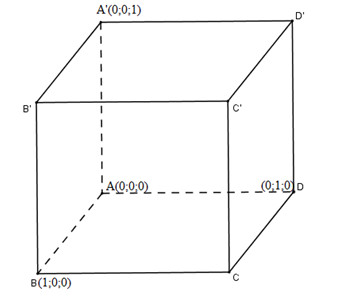
Chọn hệ trục tọa độ \(Oxyz\) sao cho \(A(0 ; 0 ; 0), B(1 ; 0 ;  0), D(0 ; 1; 0), A'(0 ; 0 ; 1)\)

Khi đó

\(B'(1 ; 0 ; 1), D'(0 ; 1 ; 1), C(1 ; 1 ; 0)\). Phương trình mặt phẳng \((A'BD)\) có dạng:

 \(x + y + z - 1 = 0\).                         (1)

\(\overrightarrow{CB'}(0 ; -1 ; 1)\) ; \(\overrightarrow{CD'}(-1 ; 0 ; 1)\).

Mặt phẳng \((B'D'C)\) qua điểm \(C\) và nhận \(\overrightarrow{n}=\left [\overrightarrow{CB'},\overrightarrow{CD'} \right ] = (-1 ; -1 ; -1 )\) làm vectơ pháp tuyến. Phương trình mặt phẳng \((B'D'C)\) có dạng:

\(x + y + z - 2 = 0\)                          (2)

Ta có \(d_{1}(A,(A'BD))=\frac{1}{\sqrt{3}}.\)

       \(d_{2}(A,(B'D'C))=\frac{2}{\sqrt{3}}.\)

Giaibaitap.me