Bài 54 trang 113 SGK Đại số và Giải tích 12 Nâng cao
Tìm đạo hàm của các hàm số sau:
a) \(y = \left( {3x - 2} \right){\ln ^2}x\);
b) \(y = \sqrt {{x^2} + 1} \ln {x^2}\);
c) \(y = x.\ln {1 \over {1 + x}}\);
d) \(y = {{\ln \left( {{x^2} + 1} \right)} \over x}\).
Giải
a) \({y'} = 3{\ln ^2}x + \left( {3x - 2} \right).{{2\ln x} \over x} = 3{\ln ^2}x + {{2\left( {3x - 2} \right)\ln x} \over x}\).
b) \({y'} = {x \over {\sqrt {{x^2} + 1} }}.\ln {x^2} + \sqrt {{x^2} + 1} .{{2x} \over {{x^2}}} = {{x\ln {x^2}} \over {\sqrt {{x^2} + 1} }} + {{2\sqrt {{x^2} + 1} } \over x}\).
c) \({y'} = \ln {1 \over {1 + x}} + x.{{ - {1 \over {{{\left( {1 + x} \right)}^2}}}} \over {{1 \over {1 + x}}}} = - \ln \left( {1 + x} \right) - {x \over {x + 1}}\).
d) \({y'} = {{{{2x} \over {{x^2} + 1}}.x - \ln \left( {{x^2} + 1} \right)} \over {{x^2}}} = {{2} \over {{x^2} + 1}} - {{\ln \left( {{x^2} + 1} \right)} \over {{x^2}}}\).
Bài 55 trang 113 SGK Đại số và Giải tích 12 Nâng cao
Trong các hàm số sau đây, hàm số nào đồng biến, hàm số nào nghịch biến trên khoảng xác định của nó?
a) \(y = {\log _{{2 \over e}}}x\);
b) \(y = {\log _a}x\) với \(a = {1 \over {3\left( {\sqrt 3 - \sqrt 2 } \right)}}\).
Giải
a) Vì \({2 \over e} < 1\) nên hàm số \(y = {\log _{{2 \over e}}}x\) nghịch biến trên \(\left( {0; + \infty } \right)\).
b) Vì \(a = {1 \over {3\left( {\sqrt 3 - \sqrt 2 } \right)}} = {{\sqrt 3 + \sqrt 2 } \over 3} > 1\) nên hàm số \(y = {\log _a}x\) đồng biến trên \(\left( {0; + \infty } \right)\).
Bài 56 trang 113 SGK Đại số và Giải tích 12 Nâng cao
Vẽ đồ thị của các hàm số sau:
a) \(y = {\log _{\sqrt 2 }}x\); b) \(y = {\log _{{2 \over 3}}}x\);
Giải
a) TXĐ: \(D = \left( {0; + \infty } \right)\)
\(a = \sqrt 2 > 1\) nên hàm số \(y = {\log _{\sqrt 2 }}x\) đồng biến trên \(\left( {0; + \infty } \right)\)
Bảng giá trị:

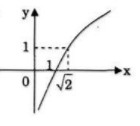
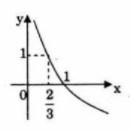
b) TXĐ: \(D = \left( {0; + \infty } \right)\)
\(a = {2 \over 3} < 1\) nên hàm số \(y = {\log _{{2 \over 3}}}x\) nghịch biến trên \(\left( {0; + \infty } \right)\)
Bảng giá trị:
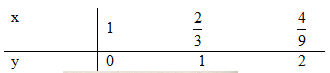
Giaibaitap.me
Giải bài tập trang 112, 113 bài 5 hàm số mũ và hàm số lôgarit SGK Giải tích 12 Nâng cao. Câu 51: Giải bài tập trang 111, 112, 113 bài 5 hàm số mũ và hàm số lôgarit SGK Giải tích 12 Nâng cao....
Giải bài tập trang 117 bài 6 hàm số lũy thừa SGK Giải tích 12 Nâng cao. Câu 57: Trên hình 2.10 cho hai đường cong ...
Giải bài tập trang 117, 118 bài 6 hàm số lũy thừa SGK Giải tích 12 Nâng cao. Câu 60: Chứng minh rằng đồ thị của hai hàm số sau đối xứng với nhau qua trục tung...
Giải bài tập trang 123, 124 bài 7 phương trình mũ và lôgarit SGK Giải tích 12 Nâng cao. Câu 63: Giải các phương trình sau:...
