Bài 51 trang 112 SGK Đại số và Giải tích 12 Nâng cao
Giải bài tập trang 111, 112, 113 bài 5 hàm số mũ và hàm số lôgarit SGK Giải tích 12 Nâng cao.:
a) \(y = {\left( {\sqrt 2 } \right)^x}\); b) \(y = {\left( {{2 \over 3}} \right)^x}\);
Giải
a) TXĐ: \(D =\mathbb R\)
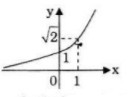
\(a = \sqrt 2 > 1\) hàm số \(y = {\left( {\sqrt 2 } \right)^x}\) đồng biến trên \(\mathbb R\)
Bảng giá trị:
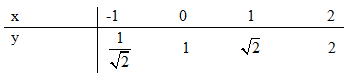
Đồ thị:
b) TXĐ: \(D =\mathbb R\)
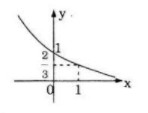
\(a = {2 \over 3} < 0\) hàm số \(y = {\left( {{2 \over 3}} \right)^x}\) nghịch biến trên \(\mathbb R\)
Bảng giá trị:

Đồ thị:
Bài 52 trang 112 SGK Đại số và Giải tích 12 Nâng cao
Sử dụng công thức \(L\left( {dB} \right) = 10\log {I \over {{I_0}}}\) (xem bài đọc thêm “Lôgarit trong một số công thức đo lường “ tr.99), hãy tính gần đúng, chính xác đến hàng đơn vị, độ lớn dB của âm thanh có tỉ số \({I \over {{I_0}}}\) cho bảng sau rồi điền vào cột còn trống:
|
STT |
Loại âm thanh |
\({I \over {{I_0}}}\) |
Độ lớn (L) |
|
1 |
Ngưỡng nghe |
1 |
|
|
2 |
Nhạc êm dịu |
400 |
|
|
3 |
Nhạc mạnh phát ra từ loa |
6,8 x 108 |
|
|
4 |
Tiếng máy bay phản lực |
2,3 x 1012 |
|
|
5 |
Ngưỡng đau tai |
1013 |
|
Giải
|
STT |
Loại âm thanh |
\({I \over {{I_0}}}\) |
Độ lớn (L) |
|
1 |
Ngưỡng nghe |
1 |
0 dB |
|
2 |
Nhạc êm dịu |
400 |
36 dB |
|
3 |
Nhạc mạnh phát ra từ loa |
6,8 x 108 |
88 dB |
|
4 |
Tiếng máy bay phản lực |
2,3 x 1012 |
124 dB |
|
5 |
Ngưỡng đau tai |
1013 |
130 dB |
Bài 53 trang 113 SGK Đại số và Giải tích 12 Nâng cao
Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to 0} {{\ln \left( {1 + 3x} \right)} \over x}\)
b) \(\mathop {\lim }\limits_{x \to 0} {{\ln \left( {1 + {x^2}} \right)} \over x}\)
Giải
a) \(\mathop {\lim }\limits_{x \to 0} {{\ln \left( {1 + 3x} \right)} \over x} = 3.\mathop {\lim }\limits_{x \to 0} {{\ln \left( {1 + 3x} \right)} \over {3x}} = 3\).
b) Vì \(\mathop {\lim }\limits_{x \to 0} {{\ln \left( {1 + {x^2}} \right)} \over {{x^2}}} = 1\) nên \(\mathop {\lim }\limits_{x \to 0} {{\ln \left( {1 + {x^2}} \right)} \over x} = \mathop {\lim }\limits_{x \to 0} x{{\ln \left( {1 + {x^2}} \right)} \over {{x^2}}} = 0.1 = 0\).
Giaibaitap.me
Giải bài tập trang 117 bài 6 hàm số lũy thừa SGK Giải tích 12 Nâng cao. Câu 57: Trên hình 2.10 cho hai đường cong ...
Giải bài tập trang 117, 118 bài 6 hàm số lũy thừa SGK Giải tích 12 Nâng cao. Câu 60: Chứng minh rằng đồ thị của hai hàm số sau đối xứng với nhau qua trục tung...
Giải bài tập trang 123, 124 bài 7 phương trình mũ và lôgarit SGK Giải tích 12 Nâng cao. Câu 63: Giải các phương trình sau:...
Giải bài tập trang 123, 124, 125 bài 7 phương trình mũ và lôgarit SGK Giải tích 12 Nâng cao. Câu 69: Giải các phương trình sau...
