Bài 2.62 trang 105 Sách bài tập (SBT) Toán Hình học 10

Cho tam giác ABC \(\widehat {BAC} = {60^ \circ }\), AB = 4 và AC = 6.

a) Tính tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AB} .\overrightarrow {BC} \), độ dài cạnh BC và bán kính R của đường tròn ngoại tiếp tam giác ABC;

b) Lấy các điểm M, N định bởi: \(2\overrightarrow {AM}  + 3\overrightarrow {MC}  = \overrightarrow 0 \) và \(\overrightarrow {NB}  + x\overrightarrow {NC}  = \overrightarrow 0 (x \ne  - 1)\). Định x để AN vuông góc với BM.

Gợi ý làm bài

a) 

\(\eqalign{
& \overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos A \cr
& = 4.6.\left( {{1 \over 2}} \right) = 12 \cr} \)

\(\eqalign{
& \overrightarrow {AB} .\overrightarrow {BC} = \overrightarrow {AB} (\overrightarrow {AC} - \overrightarrow {AB} ) \cr
& = \overrightarrow {AB} .\overrightarrow {AC} - A{B^2} = 12 - 16 = - 4 \cr
& B{C^2} = {(\overrightarrow {AC} - \overrightarrow {AB} )^2} \cr
& = A{C^2} - 2\overrightarrow {AB} .\overrightarrow {AC} + A{B^2} \cr
& = 36 - 2.12 + 16 = 28 \cr
& \Rightarrow BC = 2\sqrt {7.} \cr} \)

\(R = {{BC} \over {2\sin A}} = {{2\sqrt 7 } \over {2.{{\sqrt 3 } \over 2}}} = {{2\sqrt {21} } \over 3}.\)

b) 

\(\eqalign{
& 2\overrightarrow {AM} + 3\overrightarrow {MC} = \overrightarrow 0 \cr
& \Leftrightarrow 2\overrightarrow {AM} + 3(\overrightarrow {AC} - \overrightarrow {AM} ) = \overrightarrow 0 \cr
& \Rightarrow \overrightarrow {AM} = 3\overrightarrow {AC} \Rightarrow \overrightarrow {AB} + \overrightarrow {BM} = 3\overrightarrow {AC} \cr
& \Rightarrow \overrightarrow {BM} = 3\overrightarrow {AC} - \overrightarrow {AB} \cr} \)

và \(\eqalign{
& \overrightarrow {NB} + x\overrightarrow {NC} = \overrightarrow 0 \cr
& \Rightarrow \overrightarrow {AB} - \overrightarrow {AN} + x(\overrightarrow {AC} - \overrightarrow {AN} ) = \overrightarrow 0 \cr} \)

\( \Rightarrow \overrightarrow {AN}  = {1 \over {x + 1}}(\overrightarrow {AB}  + x\overrightarrow {AC} ).\)

AN vuông góc với BM: \(\overrightarrow {AN} .\overrightarrow {BM}  = 0\)

\(\eqalign{
& \Leftrightarrow \left( {\overrightarrow {AB} + x\overrightarrow {AC} } \right)(3\overrightarrow {AC} - \overrightarrow {AB} ) = 0 \cr
& \Leftrightarrow (3 - x)\overrightarrow {AB} .\overrightarrow {AC} - A{B^2} + 3xA{C^2} = 0 \cr
& \Leftrightarrow \left( {3 - x} \right).12 - 16 + 3x.36 = 0 \cr
& \Leftrightarrow 96x + 20 = 0 \cr
& \Leftrightarrow x = - {5 \over {24}} \cr} \)

Bài 2.63 trang 105 Sách bài tập (SBT) Toán Hình học 10

Cho tam giác ABC có a = 12, b = 16, c = 20.

a)Tính diện tích S và chiều cao \({h_a}\) của tam giác;

b)Tính độ dài đường trung tuyến \({m_a}\) của tam giác;

c)Tính bán kính R và r của các đường tròn ngoại tiếp và nội tiếp tam giác.

Gợi ý làm bài 

a) Theo công thức Hê – rông với \(p = {1 \over 2}(12 + 16 + 20) = 24\)

Ta có: \(S = \sqrt {24\left( {24 - 12} \right)\left( {24 - 16} \right)\left( {24 - 20} \right)}  = 96\)

\({h_a} = {{2S} \over a} = {{2.96} \over {12}} = 16\)

b) \(\eqalign{
& m_a^2 = {{2({b^2} + {c^2}) - {a^2}} \over 4} \cr
& = {{2\left( {{{16}^2} + {{20}^2}} \right) - {{12}^2}} \over 4} = 292 \cr} \)

\({m_a} = \sqrt {292}  \approx 17,09\)

c) \(\eqalign{
& R = {{abc} \over {4S}} = {{12.16.20} \over {4.96}} = 10; \cr
& r = {S \over p} = {{96} \over {24}} = 4 \cr} \)

Bài 2.64 trang 105 Sách bài tập (SBT) Toán Hình học 10

Hai chiếc tàu thủy P và Q cách nhau 300m. Từ P và Q thẳng hàng với chân A của tháp hải đẳng AB trên bờ biển người ta nhìn chiều cao AB của tháp dưới các góc \(\widehat {BPA} = {35^o}\) và \(\widehat {BQA} = {48^ô}\)

a)Tính BQ;

b)Tính chiều cao của tháp.

Gợi ý làm bài

a) (Xem hình 2.34) 

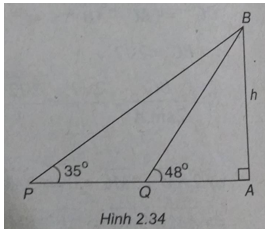
Ta có: \(\widehat {PBQ} = {48^ \circ } - {35^ \circ } = {13^ \circ }\)

Trong tam giác BPQ ta có:

\({{BQ} \over {\sin P}} = {{PQ} \over {\sin B}} \Leftrightarrow {{BQ} \over {\sin {{35}^ \circ }}} = {{300} \over {\sin {{13}^ \circ }}}\)

Do đó: \(BQ = {{300.\sin {{35}^ \circ }} \over {\sin {{13}^ \circ }}} \approx 764,935(m)\)

b) Chiều cao của tháp là

\(\eqalign{
& AB = BQ\sin {48^ \circ } \cr
& \approx 764,935.\sin {48^ \circ } \approx 568,457(m) \cr} \)

Giaibaitap.me