Bài 14 trang 40 Sách bài tập (SBT) Toán Đại số 10

Xác định trục đối xứng, tọa độ đỉnh, giao điểm với trục tung và trục hoành của parabol.

a) \(y = 2{x^2} - x - 2\)

b) \(y =  - 2{x^2} - x + 2\)

c) \(y =  - {1 \over 2}{x^2} + 2x - 1\)

d) \(y = {1 \over 5}{x^2} - 2x + 6\)

Gợi ý làm bài

a) Ở đây \(a = 2;b =  - 2;c =  - 2\) . Ta có \(\Delta  = {( - 1)^2} - 4.2.( - 2) = 17\)

Trục đối xứng là đường thẳng \(x = {1 \over 4}\) ; đỉnh \(I({1 \over 4}; - {{17} \over 8})\) giao với trục tung tại điểm (0;-2).

Để tìm giao điểm với trục hoành ta giải phương trình

\(2{x^2} - x - 2 = 0 \Leftrightarrow {x_{1,2}} = {{1 \pm \sqrt {17} } \over 4}\)

Vậy các giao điểm với trục hoành là \(({{1 + \sqrt {17} } \over 4};0)\) và \(({{1 - \sqrt {17} } \over 4};0)\)

b) Trục đối xứng \(x =  - {1 \over 4}\) ; đỉnh \(I( - {1 \over 4}; - {{17} \over 8})\) giao với trục tung tại điểm (0;2); giao với trục hoành tại các điểm \(( - {{1 + \sqrt {17} } \over 4};0)\) và \(({{\sqrt {17}  - 1} \over 4};0)\) .

c) Trục đối xứng x = 2; đỉnh I(2;1); giao với trục tung tại điểm (0;-1) giao với trục hoành tại các điểm \((1 + \sqrt 2 ;0)\) và \((2 - \sqrt 2 ;0)\)

d) Trục đối xứng x = 5; đỉnh I(5;1); giao với trục tung tại điểm (0;6). Parabol không cắt trục hoành \((\Delta  =  - {4 \over 5} < 0)\)

Bài 15 trang 40 Sách bài tập (SBT) Toán Đại số 10

Lập bảng biến thiên và vẽ đồ thị của hàm số bậc hai

a) \(y = 2{x^2} + 4x - 6\)

b) \(y =  - 3{x^2} - 6x + 4\)

c) \(y = \sqrt 3 {x^2} + 2\sqrt 3 x + 2\)

d) \(y =  - 2({x^2} + 1)\)

Gợi ý làm bài

a) Hàm số bậc hai đã cho có a = 2; b = 4; c = -6;

Vậy \( - {b \over {2a}} =  - 1;\Delta  = {b^2} - 4ac = 64; - {\Delta  \over {4a}} =  - 8\)

Vì a > 0, ta có bảng biến thiên 

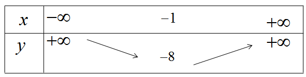
Hàm số nghịch biến trên khoảng \(( - \infty ; - 1)\) đồng biến trên khoảng \(( - 1; + \infty )\)

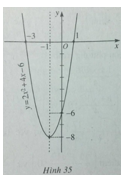
Để vẽ đồ thị ta có trục đối xứng là đường thẳng x = -1; đỉnh I(-1;-8); giao với tục tung tại điểm (0;-6); giao với trục hoành tại các điểm (-3;0) và (1;0).

Đồ thị của hàm số \(y = 2{x^2} + 4x - 6\) được vẽ trên hình 35.

b) Bảng biến thiên

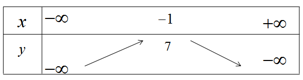
Hàm số đồng biến trên khoảng \(( - \infty ; - 1)\) và nghịch biến trên khoảng \(( - 1; + \infty )\)

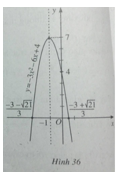
Đỉnh parabol I(-1;7). Đồ thị của hàm số \(y =  - 3{x^2} - 6x + 4\) được vẽ trên hình 36.

c) Bảng biến thiên

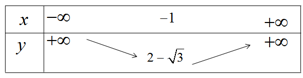
Hàm số nghịch biến trên khoảng \(( - \infty ; - 1)\) và đồng biến trên khoảng \(( - 1; + \infty )\)

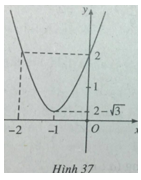
Đỉnh parabol \(( - 1;2 - \sqrt 3 )\)

Đồ thị hàm số được vẽ trên hình 37.

d) \(y =  - 2{x^2} - 2\)

Bảng biến thiên

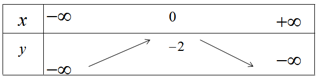
Hàm số đồng biến trên khoảng \(( - \infty ;0)\) và nghịch biến trên khoảng  \((0; + \infty )\) , hàm số là chẵn.

Đỉnh parabol I(0;-2); đồ thị đi qua điểm (1;-4) và điểm (-1;-4). 

Đồ thị hàm số \(y =  - 2({x^2} + 1)\) được vẽ trên hình 38.

Bài 16 trang 40 Sách bài tập (SBT) Toán Đại số 10

Xác định hàm số bậc hai \(y = a{x^2} - 4x + c\), biết rằng đồ thị của nó

a) Đi qua hai điểm A(1;-2) và B(2;3);

b) Có đỉnh là I(-2 ;-1) ;

c) Có hoành độ đỉnh là -3 và đi qua điểm P(-2 ;1) ;

d) Có trục đối xứng là đường thẳng x = 2 và cắt trục hoành tại điểm M(3 ;0).

Gợi ý làm bài

Các hàm số bậc hai cần xác định đều có b = -4.

a) Ta có 

\(\left\{ \matrix{
- 2 = a - 4 + c \hfill \cr
3 = 4a - 8 + c \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a + c = 2 \hfill \cr
4a + c = 11 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = 3 \hfill \cr
c = - 1 \hfill \cr} \right.\)

Vậy hàm số cần tìm là \(y = 3{x^2} - 4x - 1\)

b) \(y =  - {x^2} - 4x - 5\)

c) \(y =  - {2 \over 3}{x^2} - 4x - {{13} \over 3}\)

d) \(y = {x^2} - 4x + 3\)

Giaibaitap.me