Bài 1 trang 47 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo
Câu hỏi:
Tìm tập xác định của các hàm số sau:
a) \(f(x) = \sqrt { - 5x + 3} \)
b) \(f(x) = 2 + \frac{1}{{x + 3}}\)
Tập xác định của hàm số \(y = f(x)\) là tập hợp tất cả các số thực x sao cho biểu thức \(f(x)\) có nghĩa.
a) \(\sqrt A \) có nghĩa \( \Leftrightarrow A \ge 0\)
b) \(\frac{A}{B}\) có nghĩa \( \Leftrightarrow B \ne 0\)
a) Biểu thức \(f(x)\) có nghĩa khi và chỉ khi \( - 5x + 3 \ge 0,\)tức là khi \(x \le \frac{3}{5}.\)
Vậy tập xác định của hàm số này là \(D = ( - \infty ;\frac{3}{5}]\)
b) Biểu thức \(f(x)\) có nghĩa khi và chỉ khi \(x + 3 \ne 0,\)tức là khi \(x \ne - 3\)
Vậy tập xác định của hàm số này là \(D = \mathbb{R}\backslash \left\{ { - 3} \right\}\)
Bài 2 trang 47 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo
Câu hỏi:
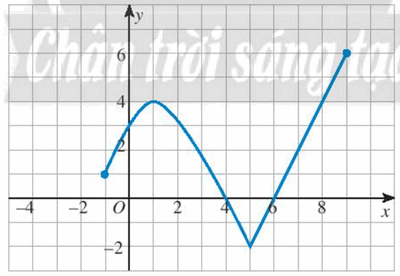
Tìm tập xác định, tập giá trị của hàm số có đồ thị như Hình 10.
Phương pháp:
+) Tập xác định là tập hợp các giá trị của biến số x.
+) Tập giá trị là tập hợp các giá trị y (tương ứng với x thuộc tập xác định)
Từ đồ thị trên, ta thấy hàm số xác định trên [-1; 9].
Do đó tập xác định của hàm số là D = [-1; 9].
Giá trị thấp nhất của y = f(x) là – 2 tương ứng với x = 5 và giá trị cao nhất của y = f(x) là 6 tương ứng với x = 9.
Do đó tập giá trị của hàm số là [-2; 6].
Bài 3 trang 47 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo
Câu hỏi:
Tìm các khoảng đồng biến, nghịch biến của các hàm số sau:
a) \(f(x) = - 5x + 2\)
b) \(f(x) = - {x^2}\)
Bước 1: Lấy \({x_1},{x_2} \in D\) là hai số tùy ý sao cho \({x_1} < {x_2}\).
Bước 2: Tìm điều kiện để \(f({x_1}) < f({x_2})\) và \(f({x_1}) > f({x_2})\)
a) \(f({x_1}) = - 5{x_1} + 2,f({x_2}) = - 5{x_2} + 2\)
b) \(f({x_1}) = - {x_1}^2,f({x_2}) = - {x_2}^2\)
Bước 3: Kết luận khoảng đồng biến, nghịch biến
+ \(f({x_1}) < f({x_2})\) với \(x \in {T_1}\) thì hàm số đồng biến trên khoảng \({T_1}\)
+ \(f({x_1}) > f({x_2})\) với \(x \in {T_2}\) thì hàm số nghịch biến trên khoảng \({T_2}\)
a)
Tập xác định D = R
Lấy x1 , x2 là hai số thực tùy ý thỏa mãn x1 < x2, ta có:
f(x1) – f(x2) = (-5x1 + 2) – (-5x2 + 2) = -5x1 + 2 + 5x2 – 2 = -5x1 + 5x2 = 5(x2 – x1)
Vì x1 < x2 ⇒ 5(x2 – x1) > 0 ⇒ f(x1) – f(x2) > 0 hay f(x1) > f(x2).
Vậy hàm số nghịch biến (giảm) trên R
b)
Tập xác định D = R
Lấy x1 , x2 là hai số thực tùy ý thỏa mãn x1 < x2, ta có:
f(x1) – f(x2) = - x12 – (-x22) = x22 - x12 = (x2 – x1)(x2 + x1)
+) Với x1, x2 ∈ (-∞; 0) và x1 < x2, khi đó: x1 + x2 < 0 và x2 – x1 > 0
Do đó, f(x1) – f(x2) < 0 ⇒ f(x1) < f(x2),, nên hàm số f(x) đồng biến trên khoảng (-∞; 0).
+) Với x1, x2 ∈ (-∞; 0) và x1 < x2, khi đó: x1 + x2 > 0 và x2 – x1 > 0
Do đó, f(x1) – f(x2) > 0 ⇒ f(x1) > f(x2) nên hàm số f(x) nghịch biến trên khoảng (0; +∞).
Vậy hàm số f(x) = -x2 đồng biến trên khoảng (-∞; 0) và nghịch biến trên khoảng (0; +∞).
Bài 4 trang 47 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo
Câu hỏi:
Vẽ đồ thị hàm số \(f\left( x \right) = \left| x \right|\) biết rằng hàm số này còn được viết như sau:
\(f(x) = \left\{ \begin{array}{l}x\quad \quad (x \ge 0)\\ - x\quad \;\;(x < 0)\end{array} \right.\)
Vẽ đồ thị từng hàm trên mỗi khoảng cho trước.
Trả lời:
Tập xác định của hàm số D = R
Ta có:
Với x = 0 thì f(0) = 0, ta được điểm O(0; 0).
Với x = 1 thì f(1) = 1, ta được điểm A(1; 1).
Với x = 2 thì f(2) = 2, ta được điểm B(2; 2).
Với x = 3 thì f(3) = 3, ta được điểm C(3; 3).
Với x = -1 thì f(-1) = - (-1) = 1, ta được điểm D(-1; 1).
Với x = -2 thì f(-2) = - (-2) = 2, ta được điểm E(-2; 2).
Với x = -3 thì f(-3) = - (-3) = 3, ta được điểm F(-3; 3).
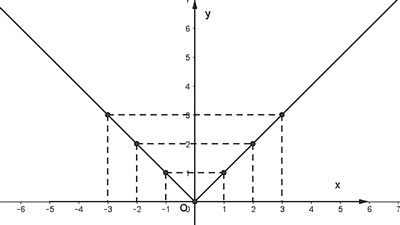
Từ các điểm O(0; 0), A(1; 1), B(2; 2), C(3; 3), D(-1; 1), E(-2; 2), F(-3; 3) ta vẽ được đồ thị hàm số f(x) = |x| như sau:
Bài 5 trang 48 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo
Câu hỏi:
Tìm tập xác định, tập giá trị và vẽ đồ thị hàm số:
\(f(x) = \left\{ \begin{array}{l} - 1\quad \quad x < 0\\1\;\quad \quad \;{\kern 1pt} x > 0\end{array} \right.\quad \)
+) Tập xác định là tập hợp các giá trị của x để f(x) có nghĩa.
+) Tập giá trị là tập hợp các giá trị của f(x) với x thuộc tập xác định.
+) Vẽ đồ thị từng hàm trên mỗi khoảng cho trước
Trả lời:
+) Dễ thấy: hàm số được xác định với mọi \(x > 0\) và \(x < 0\).
Do đó tập xác định của hàm số là \(D = \mathbb{R}{\rm{\backslash }}\{ 0\} \)
+) Với \(x \in D\):
+ Nếu \(x > 0\) thì \(f(x) = 1\)
+ Nếu \(x < 0\) thì \(f(x) = - 1\)
Vậy tập giá trị của hàm số là \(T = \{ - 1;1\} \)
+) Vẽ đồ thị hàm số:
Với \(x \in ( - \infty ;0)\) đồ thị hàm số là đường thẳng \(y = - 1\)
Với \(x \in (0; + \infty )\) đồ thị hàm số là đường thẳng \(y = 1\)
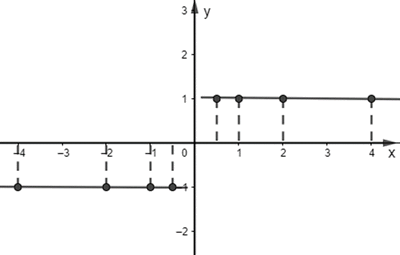
Ta được đồ thị hàm số như hình trên.
Bài 6 trang 48 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo
Câu hỏi:
Một hãng taxi có bảng giá như sau:
|
|
Giá mở cửa (0,5 km) |
Giá cước các kilomet tiếp theo |
Giá cước từ kilomet thứ 31 |
|
Taxi 4 chỗ |
11 000 đồng |
14 500 đồng |
11 600 đồng |
|
Taxi 7 chỗ |
11 000 đồng |
15 500 đồng |
13 600 đồng |
a) Xem số tiền đi taxi là một hàm số phụ thuộc số kilomet di chuyển, hãy viết công thức của các hàm số dựa trên thông tin từ bảng giá đã cho theo từng yêu cầu:
i) Hàm số \(f(x)\) để tính số tiền hành khách phải trả khi di chuyển \(x\) km bằng xe taxi 4 chỗ.
ii) Hàm số \(g(x)\) để tính số tiền hành khách phải trả khi di chuyển \(x\) km bằng xe taxi 7 chỗ.
b) Nếu cần đặt xe taxi cho 30 hành khách, nên đặt toàn bộ xe 4 chỗ hay xe 7 chỗ thì có lợi hơn?
a) Viết công thức tính tiền trong mỗi trường hợp (theo số km), từ đó suy ra hàm số nhiều công thức tương ứng.
b) Tính số tiền phải trả trong mỗi trường hợp, từ đó đưa ra lời khuyên về chọn xe.
a)
i) Khi di chuyển bằng xe taxi 4 chỗ:
Nếu x ≤ 0,5 thì số tiền hành khách phải trả là: 11 000x (nghìn đồng).
Nếu 0,5 < x < 31 thì số tiền hành khách phải trả là: 11 000.0,5 + 14 500(x – 0,5) = 14 500x – 1 750 (nghìn đồng).
Nếu x ≥ 31 thì số tiền hành khách phải trả là: 11 000.0,5 + 14 500(31 – 0,5) + 11 600(x – 31) = 11 600x + 88 150 (nghìn đồng).
Vậy hàm số f(x) được xác định như sau:
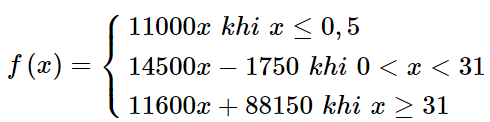
ii) Khi di chuyển bằng xe taxi 7 chỗ:
Nếu x ≤ 0,5 thì số tiền hành khách phải trả là: 11 000x (nghìn đồng).
Nếu 0,5 < x < 31 thì số tiền hành khách phải trả là: 11 000.0,5 + 15 500(x – 0,5) = 15 500x – 2 250 (nghìn đồng).
Nếu x ≥ 31 thì số tiền hành khách phải trả là: 11 000.0,5 + 15 500(31 – 0,5) + 13 600(x – 31) = 13 600x + 56 650 (nghìn đồng).
Vậy hàm số g(x) được xác định như sau:
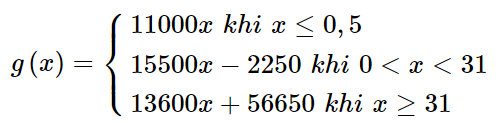
b) Có tất cả 30 hành khách nếu đặt xe 4 chỗ thì cần 8 xe, còn nếu đặt xe 7 chỗ thì cần 5 xe.
Với x ≤ 0,5, ta có:
Số tiền hành khách phải trả khi thuê xe 4 chỗ là: 8.11 000x = 88 000x (nghìn đồng).
Số tiền hành khách phải trả khi thuê xe 7 chỗ là: 5.11 000x = 55 000x (nghìn đồng).
Vì 55 000 < 88 000 nên 55 000x < 88 000x.
Do đó nếu quãng đường di chuyển nhỏ hơn 0,5km thì nên đặt xe 7 chỗ thì có lợi hơn.
Với 0,5 < x < 31, ta có:
Số tiền hành khách phải trả khi thuê xe 4 chỗ là: 8.(14 500x – 1 750) = 116 000x – 14 000 (nghìn đồng).
Số tiền hành khách phải trả khi thuê xe 7 chỗ là: 5.(15 500x – 2 250) = 77 500x – 11 250 (nghìn đồng).
Ta có: 44 000 < 116 000x – 14 000 < 3 582 000 và 27 500 < 77 500x – 11 250 < 2 391 250.
Do đó nếu quãng đường di chuyển lớn hơn 0,5km và nhỏ hơn 31km thì nên đặt xe 7 chỗ thì có lợi hơn.
Với x ≥ 31, ta có:
Số tiền hành khách phải trả khi thuê xe 4 chỗ là: 8.(11 600x + 88 150) = 92 800x + 705 200 (nghìn đồng).
Số tiền hành khách phải trả khi thuê xe 7 chỗ là: 5.(13 600x + 56 650) = 68 000x + 183 250 (nghìn đồng).
Ta có: 92 800x + 705 200 ≥ 68 000x + 183 250 .
Do đó nếu quãng đường di chuyển lớn hơn 0,5km và nhỏ hơn 31km thì nên đặt xe 7 chỗ thì có lợi hơn.
Vậy nếu đặt xe taxi cho 30 hành khách thì nên đặt toàn bộ xe 7 chỗ thì có lợi hơn.
Câu hỏi:
Số 2 đã trải qua hành trình thú vị và bị biến đổi sau khi đi qua chiếc hộp đen.

Bác thợ máy đã giải mã hộp đen cho một số x bất kì như sau:
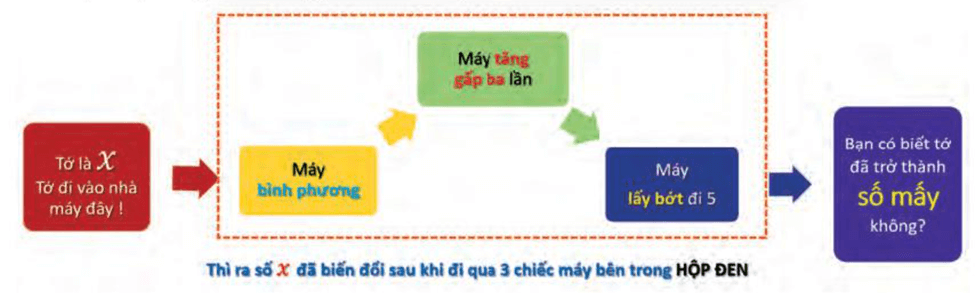
Bên trong hộp đen là một đoạn chương trình được cài đặt sẵn. Ta xem đoạn chương trình này như một hàm số f(x). Hãy viết biểu thức của f(x) để mô tả sự biến đổi đã tác động lên x.
Trả lời:
Sự biến đổi đã tác động lên x như sau:
Khi x đi qua máy bình phương x biến đổi thành x2;
Tiếp tục đi qua máy tăng gấp ba lần ta được 3x2;
Tiếp sau đó đi qua máy lấy bớt đi 5 ta được 3x2 – 5;
Vậy f(x) = 3x2 – 5.
Giaibaitap.me
Giải bài tập Toán 10 trang 56, 57 Chân trời sáng tạo tập 1 - Bài 2: Hàm số bậc hai sách. Bài 1: Hàm số nào sau đây là hàm số bậc hai?
Giải bài tập Toán 10 trang 59 Chân trời sáng tạo tập 1 - Bài tập cuối chương 3. Bài 2: Tìm điều kiện của m để mỗi hàm số sau đây là một hàm số bậc hai:
Giải bài tập Toán 10 trang 65 Chân trời sáng tạo tập 1 - Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Bài 4 : Cho tam giác ABC. Chứng minh rằng: a) sinA = sin(B + C); b) cosA = – cos(B + C).
Giải bài tập Toán 10 trang 72, 73 Chân trời sáng tạo tập 1 - Bài 2: Định lí côsin và định lí sin. Bài 1 : Tính độ dài cạnh x trong các tam giác sau :
