Bài 1 trang 72 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo
Câu hỏi:
Tính độ dài cạnh x trong các tam giác sau:
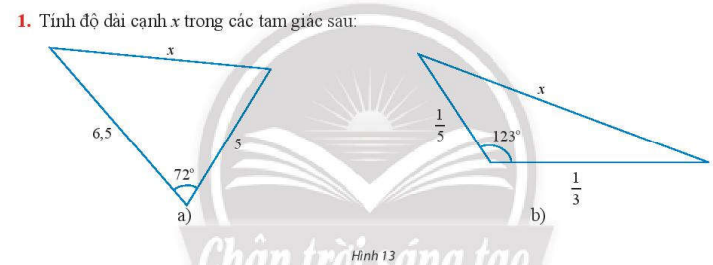
Phương pháp:
Áp dụng định lí cosin
Trả lời:
a) Áp dụng định lí cosin, ta có:
\(\begin{array}{*{20}{l}}
{{x^2} = 6,{5^2} + {5^2} - 2.6,5.5.\cos {{72}^o} \approx 47,16}\\
{ \Leftrightarrow x = \sqrt {47,16} \approx 6,87}
\end{array}\)
b) Áp dụng định lí cosin, ta có:
\(\begin{array}{l}{x^2} = {\left( {\frac{1}{5}} \right)^2} + {\left( {\frac{1}{3}} \right)^2} - 2.\frac{1}{5}.\frac{1}{3}.\cos {123^o} \approx 0,224\\ \Leftrightarrow x = \sqrt {0,224} \approx 0,473\end{array}\)
Bài 2 trang 72 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo
Câu hỏi:
Tính độ dài cạnh c trong tam giác ABC ở Hình 14.
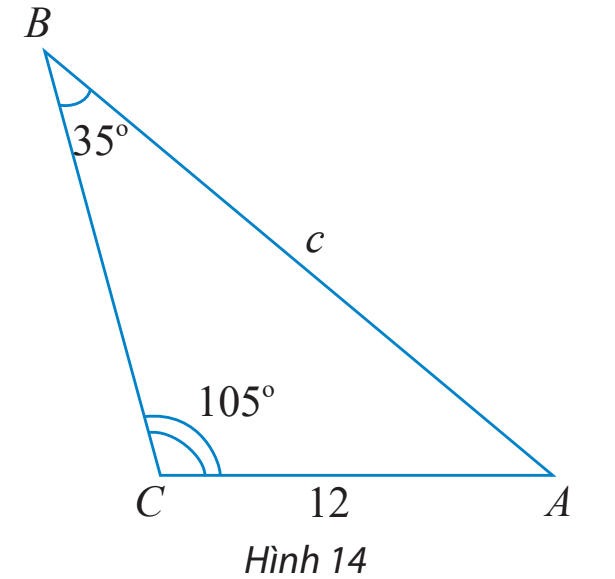
Phương pháp:
Áp dụng định lí sin:
\(\frac{AB}{{\sin C}} = \frac{{AC}}{{\sin {B}}}\)
Trả lời:
Áp dụng định lí sin, ta có:
\(\frac{c}{{\sin {{105}^o}}} = \frac{{12}}{{\sin {{35}^o}}} \Rightarrow c = \frac{{12.\sin {{105}^o}}}{{\sin {{35}^o}}} \approx 20,2\)
Bài 3 trang 72 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo
Câu hỏi:
Cho tam giác ABC, biết cạnh \(a = 152,\;\widehat B = {79^o},\;\widehat C = {61^o}.\) Tính các góc, các cạnh
còn lại và bán kính đường tròn ngoại tiếp của tam giác đó.
Phương pháp:
Áp dụng định lí sin:
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
Trả lời:
Tam giác ABC có
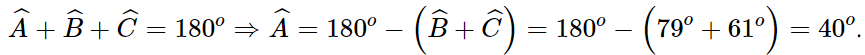
Áp dụng định lí sin ta có:
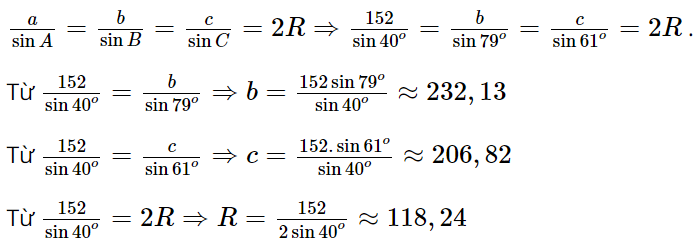
Vậy góc và các cạnh còn lại, bán kính đường tròn ngoại tiếp của tam giác ABC là:
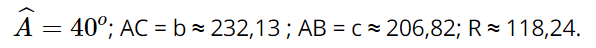
Bài 4 trang 73 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo
Câu hỏi:
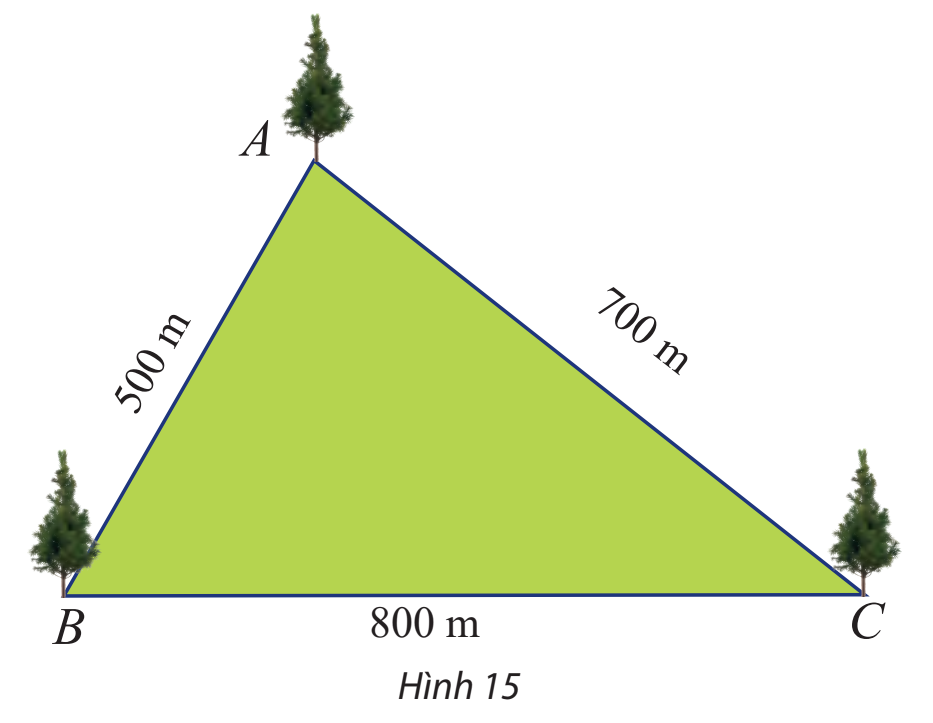
Một công viên có dạng hình tam giác với các kích thước như Hình 15. Tính số đo các góc của tam giác đó.
Phương pháp:
Áp dụng định lí cosin để tính góc:
\(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}.\)
Trả lời:
Đặt \(a = BC,b = AC,c = AB\)
Ta có: \(a = 800,b = 700,c = 500.\)
Áp dụng định lí cosin, ta có:
\(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}.\)
Suy ra:
\(\begin{array}{l}\cos A = \frac{{{{700}^2} + {{500}^2} - {{800}^2}}}{{2.700.500}} = \frac{1}{7} \Rightarrow \widehat A = {81^o}47'12,44'';\\\cos B = \frac{{{{500}^2} + {{800}^2} - {{700}^2}}}{{2.500.800}} = \frac{1}{2} \Rightarrow \widehat B = {60^o};\\\cos C = \frac{{{{800}^2} + {{700}^2} - {{500}^2}}}{{2.800.700}} = \frac{{11}}{{14}} \Rightarrow \widehat C = {38^o}12'47,56''.\end{array}\)
Vậy \(\widehat A = {81^o}47'12,44'';\widehat B = {60^o};\widehat C = {38^o}12'47,56''.\)
Bài 5 trang 73 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo
Câu hỏi:
Tính diện tích một lá cờ hình tam giác cân có độ dài cạnh bên là 90 cm và góc ở đỉnh là \({35^o}.\)

Phương pháp:
Tính diện tích bằng công thức: \(S = \frac{1}{2}bc\sin A\)
Trả lời:
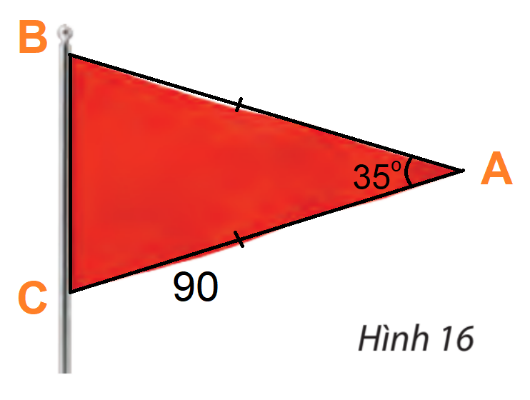
Kí hiệu các điểm A, B, C như hình trên.
Từ giả thiết ta có: \(AB = AC = 90,\widehat A = {35^o}\)
Áp dụng công thức \(S = \frac{1}{2}bc\sin A\), ta có: \(S = \frac{1}{2}.90.90.\sin {35^o} \approx 2323\;(c{m^2})\)
Bài 6 trang 73 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo
Câu hỏi:
Cho tam giác ABC có \(AB = 6,AC = 8\) và \(\widehat A = {60^o}.\)
a) Tính diện tích tam giác ABC.
b) Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Tính diện tích tam giác IBC.
Phương pháp:
a) Tính diện tích bằng công thức: \(S = \frac{1}{2}bc\sin A\)
b) Tìm a, từ đó suy ra R bằng định lí sin => Tính diện tích tam giác IBC
Trả lời:
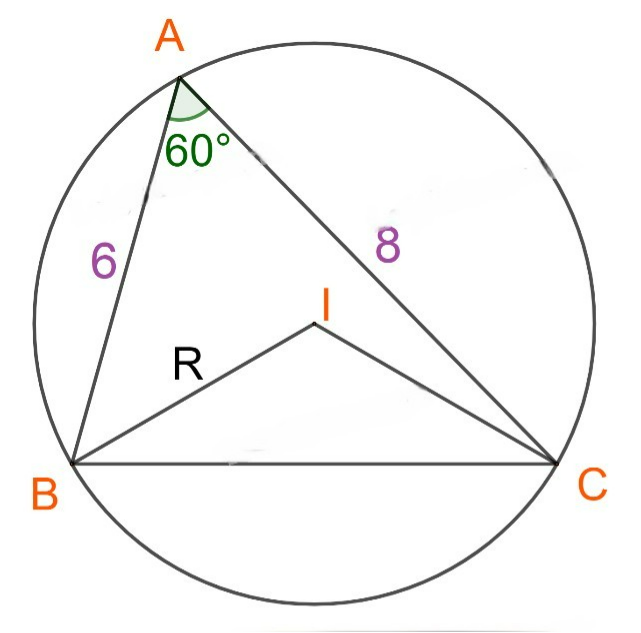
Đặt \(a = BC,b = AC,c = AB.\)
a) Áp dụng công thức \(S = \frac{1}{2}bc\sin A\), ta có: \({S_{ABC}} = \frac{1}{2}.8.6.\sin {60^o} = \frac{1}{2}.8.6.\frac{{\sqrt 3 }}{2} = 12\sqrt 3 \)
b) Áp dụng định lí cosin cho tam giác ABC ta được:
\(\begin{array}{l}B{C^2} = {a^2} = {8^2} + {6^2} - 2.8.6.\cos {60^o} = 52\\ \Rightarrow BC = 2\sqrt {13} \end{array}\)
Xét tam giác IBC ta có:
Góc \(\widehat {BIC} = 2.\widehat {BAC} = {120^o}\)(góc ở tâm và góc nội tiếp cùng chắn một cung)
\(IB = IC = R = \frac{a}{{2\sin A}} = \frac{{2\sqrt {13} }}{{2.\frac{{\sqrt 3 }}{2}}} = \frac{{2\sqrt {39} }}{3}.\)
\( \Rightarrow {S_{IBC}} = \frac{1}{2}.\frac{{2\sqrt {39} }}{3}.\frac{{2\sqrt {39} }}{3}\sin {120^o} = \frac{{13\sqrt 3 }}{3}.\)
Bài 7 trang 73 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo
Câu hỏi:
Cho tam giác ABC có trọng tâm G và độ dài ba cạnh AB, BC, CA lần lượt là 15, 18, 27.
a) Tính diện tích và bán kính đường tròn nội tiếp tam giác ABC.
b) Tính diện tích tam giác GBC.
Phương pháp:
a) Tính r bằng công thức: \(S = p.r\). Trong đó S tính bởi công thức heron.
b) Tìm a, từ đó suy ra R bằng định lí sin => Tính diện tích tam giác IBC
Trả lời:
a) Đặt \(a = BC,b = AC,c = AB.\)
Ta có: \(p = \frac{1}{2}(15 + 18 + 27) = 30\)
Áp dụng công thức heron, ta có:
\({S_{ABC}} = \sqrt {30(30 - 15)(30 - 18)(30 - 27)} = 90\sqrt 2 \)
Và \(r = \frac{S}{p} = \frac{{90\sqrt 2 }}{{30}} = 3\sqrt 2 \)
b) Gọi, H, K lần lượt là chân đường cao hạ từ A và G xuống BC, M là trung điểm BC.
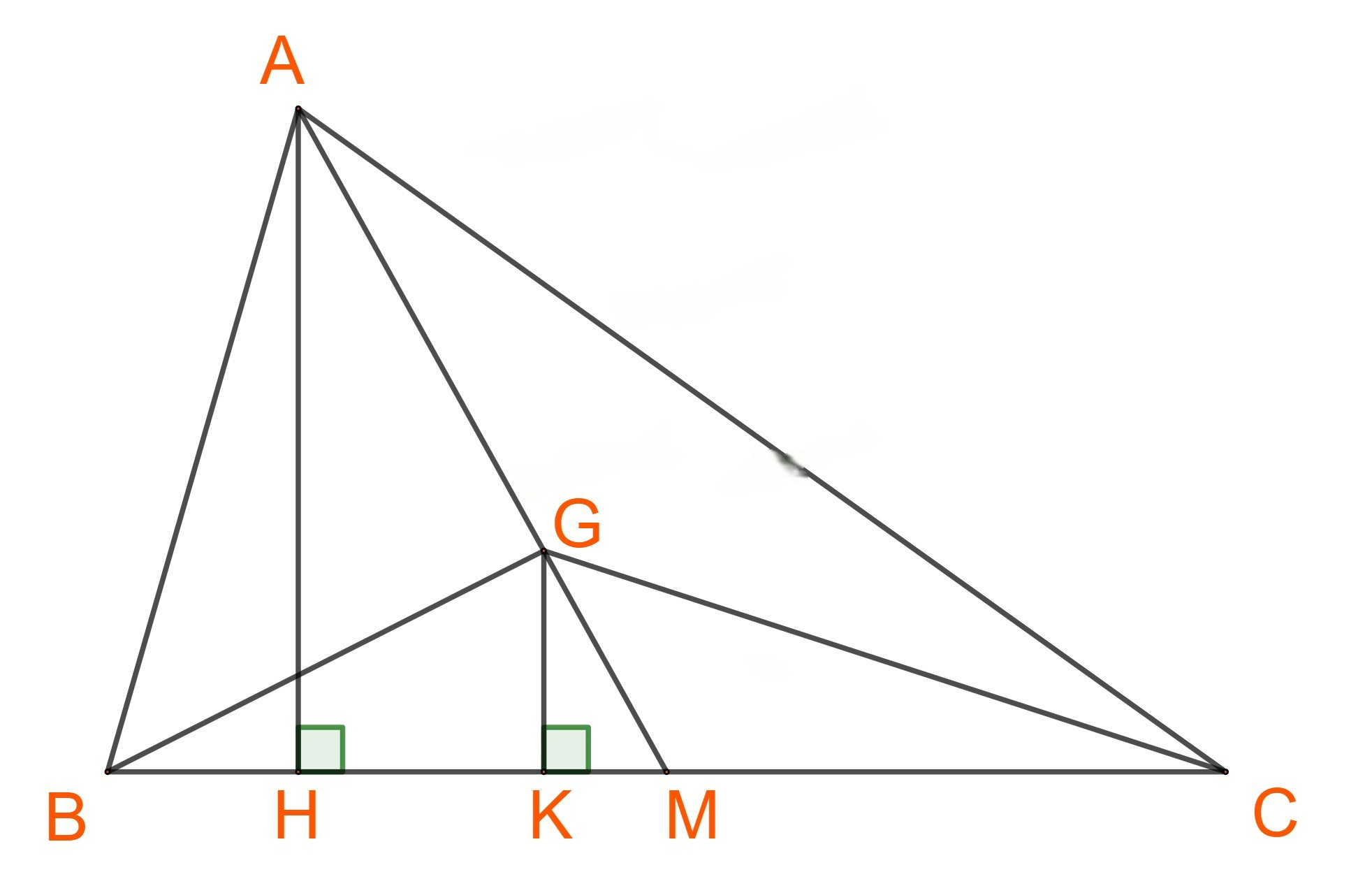
G là trọng tâm tam giác ABC nên \(GM = \frac{1}{3}AM\)
\(\begin{array}{l} \Rightarrow GK = \frac{1}{3}.AH\\ \Rightarrow {S_{GBC}} = \frac{1}{3}.\,{S_{ABC}} = \frac{1}{3}.90\sqrt 2 = 30\sqrt 2 .\end{array}\)
Câu hỏi:
Cho \({h_a}\) là đường cao vẽ từ đỉnh A, R là bán kính đường tròn ngoại tiếp tam giác ABC. Chứngminh hệ
thức: \({h_a} = 2R\sin B\sin C.\)
Phương pháp:
Bước 1: Tính \({h_a}\) theo b và sinC
Bước 2: Tính b theo R và sinB. Từ đó suy ra điều phải chứng minh.
Trả lời:
Đặt \(a = BC,b = AC,c = AB\)
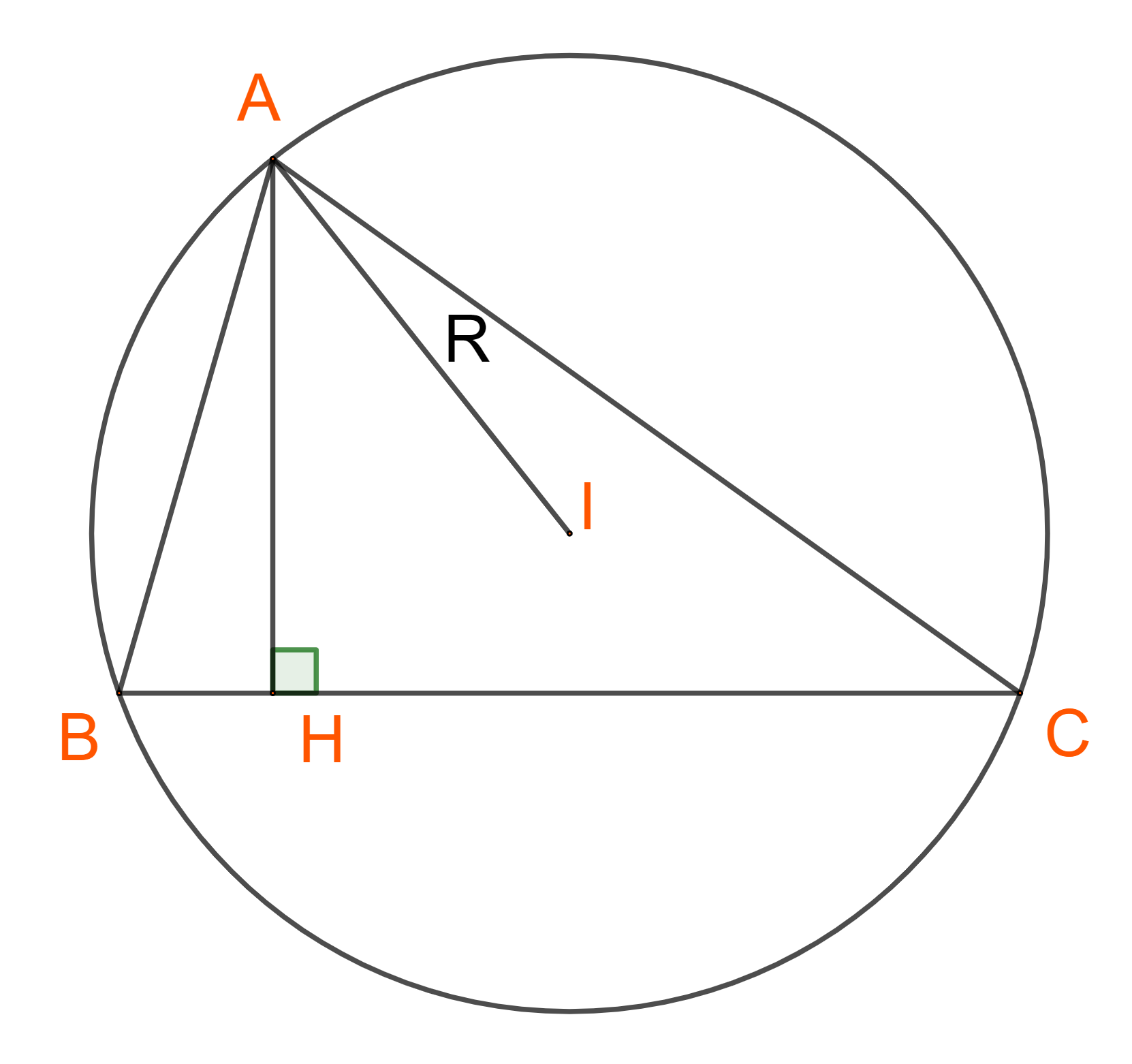
Ta có: \(\sin C = \frac{{AH}}{{AC}} = \frac{{{h_a}}}{b} \Rightarrow {h_a} = b.\sin C\)
Theo định lí sin, ta có: \(\frac{b}{{\sin B}} = 2R \Rightarrow b = 2R.\sin B\)
\( \Rightarrow {h_a} = 2R.\sin B.\sin C\)
Câu hỏi:
Cho tam giác ABC có góc B nhọn, AD và CE là hai đường cao.
a) Chứng minh \(\frac{{{S_{BDE}}}}{{{S_{BAC}}}} = \frac{{BD.BE}}{{BA.BC}}.\)
b) Biết rằng \({S_{ABC}} = 9{S_{BDE}}\) và \(DE = 2\sqrt 2 .\) Tính \(\cos B\) và bán kính đường tròn ngoại
tiếp tam giác ABC.
Phương pháp:
a) Tính diện tích bằng công thức \(S = \frac{1}{2}ac.\sin B\)
b) \(\cos B = \frac{{BD}}{{BA}} = \frac{{BE}}{{BC}}\)
Trả lời:

a) Áp dụng công thức \(S = \frac{1}{2}ac.\sin B\) cho tam giác ABC và BED, ta có:
\({S_{ABC}} = \frac{1}{2}.BA.BC.\sin B;{S_{BED}} = \frac{1}{2}..BE.BD.\sin B\)
\( \Rightarrow \frac{{{S_{BED}}}}{{{S_{ABC}}}} = \frac{{\frac{1}{2}.BE.BD.\sin B}}{{\frac{1}{2}.BA.BC.\sin B}} = \frac{{BE.BD}}{{BA.BC}}\)
b) Ta có: \(\cos B = \frac{{BD}}{{BA}} = \frac{{BE}}{{BC}}\)
Mà \(\frac{{{S_{BED}}}}{{{S_{ABC}}}} = \frac{1}{9} \Rightarrow \frac{{BD}}{{BA}}.\frac{{BE}}{{BC}} = \frac{1}{9}\)
\( \Rightarrow \cos B = \frac{{BD}}{{BA}} = \frac{{BE}}{{BC}} = \frac{1}{3}\)
+) Xét tam giác ABC và tam giác DEB ta có:
\(\frac{{BE}}{{BC}} = \frac{{BD}}{{BA}} = \frac{1}{3}\) và góc B chung
\( \Rightarrow \Delta ABC \sim \Delta DEB\) (cgc)
\( \Rightarrow \frac{{DE}}{{AC}} = \frac{1}{3} \Rightarrow AC = 3.DE = 3.2\sqrt 2 = 6\sqrt 2 .\)
Ta có: \(\cos B = \frac{1}{3} \Rightarrow \sin B = \sqrt {1 - {{\left( {\frac{1}{3}} \right)}^2}} = \frac{{2\sqrt 2 }}{3}\) (do B là góc nhọn)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AC}}{{\sin B}} = 2R \Rightarrow R = \frac{{6\sqrt 2 }}{{\frac{{2\sqrt 2 }}{3}}}:2 = \frac{9}{2}\)
Bài 10 trang 73 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo
Câu hỏi:
Cho tứ giác lồi ABCD có các đường chéo \(AC = x,BD = y\) và góc giữa AC và BD bằng \(\alpha .\) Gọi S là diện
tích của tứ giác ABCD.
a) Chứng minh \(S = \frac{1}{2}xy.\sin \alpha \)
b) Nêu kết quả trong trường hợp \(AC \bot BD.\)
Phương pháp:
a) Tính diện tích 4 tam giác nhỏ theo \(\sin \alpha \).
Chú ý: \(\sin ({180^o} - \alpha ) = \sin \alpha \)
b) \(\alpha = {90^o}\) thì \(\sin \alpha = 1\)
Trả lời:
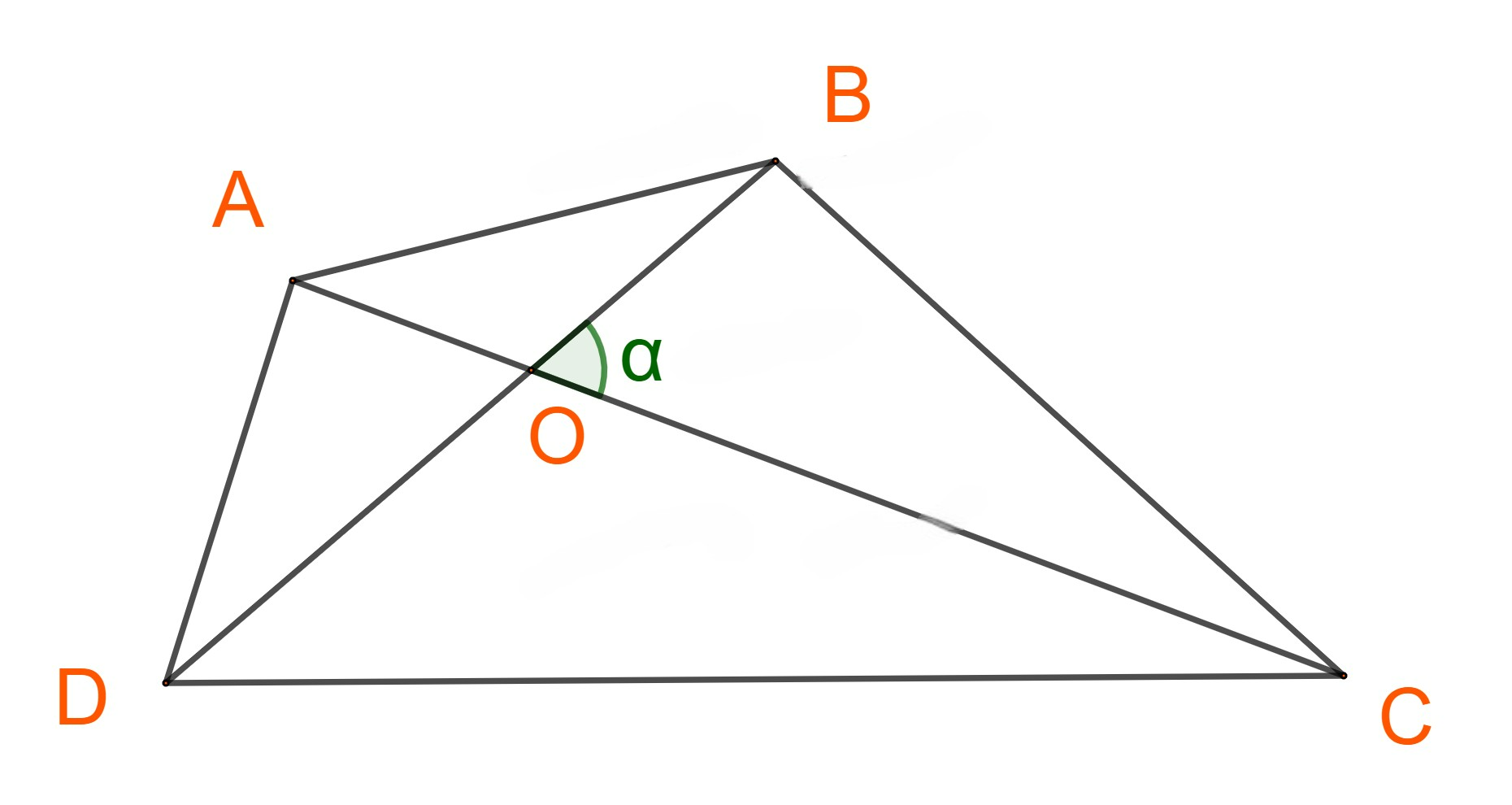
Gọi O là giao điểm của AC và BD.
a) Áp dụng công thức \(S = \frac{1}{2}ac.\sin B\), ta có:
\(\begin{array}{l}{S_{OAD}} = \frac{1}{2}.OA.OD.\sin \alpha ;\quad {S_{OBC}} = \frac{1}{2}.OB.OC.\sin \alpha ;\\{S_{OAB}} = \frac{1}{2}.OA.OB.\sin ({180^o} - \alpha );\quad {S_{OCD}} = \frac{1}{2}.OD.OC.\sin ({180^o} - \alpha ).\end{array}\)
Mà \(\sin ({180^o} - \alpha ) = \sin \alpha \)
\( \Rightarrow {S_{OAB}} = \frac{1}{2}.OA.OB.\sin \alpha ;\quad {S_{OCD}} = \frac{1}{2}.OD.OC.\sin \alpha .\)
\(\begin{array}{l} \Rightarrow {S_{ABCD}} = \left( {{S_{OAD}} + {S_{OAB}}} \right) + \left( {{S_{OBC}} + {S_{OCD}}} \right)\\ = \frac{1}{2}.OA.\sin \alpha .(OD + OB) + \frac{1}{2}.OC.\sin \alpha .(OB + OD)\\ = \frac{1}{2}.OA.\sin \alpha .BD + \frac{1}{2}.OC.\sin \alpha .BD\\ = \frac{1}{2}.BD.\sin \alpha .(OA + OC)\\ = \frac{1}{2}.AC.BD.\sin \alpha = \frac{1}{2}.x.y.\sin \alpha .\end{array}\)
b) Nếu \(AC \bot BD\) thì \(\alpha = {90^o} \Rightarrow \sin \alpha = 1.\)
\( \Rightarrow {S_{ABCD}} = \frac{1}{2}.x.y.1 = \frac{1}{2}.x.y.\)
Giaibaitap.me
Giải bài tập Toán 10 trang 77, 78 Chân trời sáng tạo tập 1 - Bài 3: Giải tam giác và ứng dụng thực tế. Bài 1 : Giải tam giác ABC trong các trường hợp sau:
Giải bài tập Toán 10 trang 78, 79 Chân trời sáng tạo tập 1 - Bài tập cuối chương 4. Bài 5 : Cho hình bình hành ABCD. a) Chứng minh 2(AB2 + BC2) = AC2 + BD2.
Giải bài tập Toán 10 trang 86, 87 Chân trời sáng tạo tập 1 - Bài 1: Khái niệm vectơ. Bài 1: a) Bạn hãy tìm sự khác biệt giữa hai đại lượng sau: - Bác Ba có số tiền là 20 triệu đồng. - Một cơn bão di chuyển với vận tốc 20 km/h theo hướng đông bắc.
Giải bài tập Toán 10 trang 93 Chân trời sáng tạo tập 1 - Bài 2: Tổng và hiệu của hai vectơ. Bài 1 : Cho hình bình hành ABCD có O là giao điểm của hai đường chéo và một điểm M tùy ý. Chứng minh rằng:
