Bài 1 trang 65 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo
Câu hỏi:
Cho biết \(\sin {30^o} = \frac{1}{2};\sin {60^o} = \frac{{\sqrt 3 }}{2};\tan {45^o} = 1.\) Sử dụng mối liên hệ giữa các giá trị lượng giác của hai góc bù nhau, phụ nhau để tính giá trị của \(E = 2\cos {30^o} + \sin {150^o} + \tan {135^o}.\)
Phương pháp:
\(\begin{array}{l}\cos {30^o} = \sin \left( {{{90}^o} - {{30}^o}} \right) = \sin {60^o}\\\sin {150^o} = \sin \left( {{{180}^o} - {{150}^o}} \right) = \sin {30^o}\\\tan {135^o} = - \tan \left( {{{180}^o} - {{135}^o}} \right) = - \tan {45^o}\end{array}\)
Ta có:
\(\begin{array}{l}\cos {30^o} = \sin \left( {{{90}^o} - {{30}^o}} \right) = \sin {60^o} = \frac{{\sqrt 3 }}{2};\\\sin {150^o} = \sin \left( {{{180}^o} - {{150}^o}} \right) = \sin {30^o} = \frac{1}{2};\\\tan {135^o} = - \tan \left( {{{180}^o} - {{135}^o}} \right) = - \tan {45^o} = - 1\end{array}\)
\( \Rightarrow E = 2.\frac{{\sqrt 3 }}{2} + \frac{1}{2} - 1 = \sqrt 3 - \frac{1}{2}.\)
Câu hỏi:
Chứng minh các hệ thức sau:
a) \(\sin {20^o} = \sin {160^o}\)
b) \(\cos {50^o} = - \cos {130^o}\)
\(\begin{array}{l}\sin \left( {{{180}^o} - \alpha } \right) = \sin \alpha \\\cos \left( {{{180}^o} - \alpha } \right) = - \cos \alpha \end{array}\)\(({0^o} \le \alpha \le {180^o})\)
a) Ta có sin20° = sin(180° – 20°) = sin160° (hai góc bù nhau).
Vậy sin20° = sin160°.
b) Ta có: cos50° = – cos(180° – 50°) = – cos130° (hai góc bù nhau).
Vậy cos50° = – cos 130°.
Bài 3 trang 65 SGK Toán lớp 10 tập 1 - Chân trời sáng tạo
Câu hỏi:
Tìm góc \(\alpha \;\;({0^o} \le \alpha \le {180^o})\) trong mỗi trường hợp sau:
a) \(\cos \alpha = - \frac{{\sqrt 2 }}{2}\)
b) \(\sin \alpha = 0\)
c) \(\tan \alpha = 1\)
d) \(\cot \alpha \) không xác định.
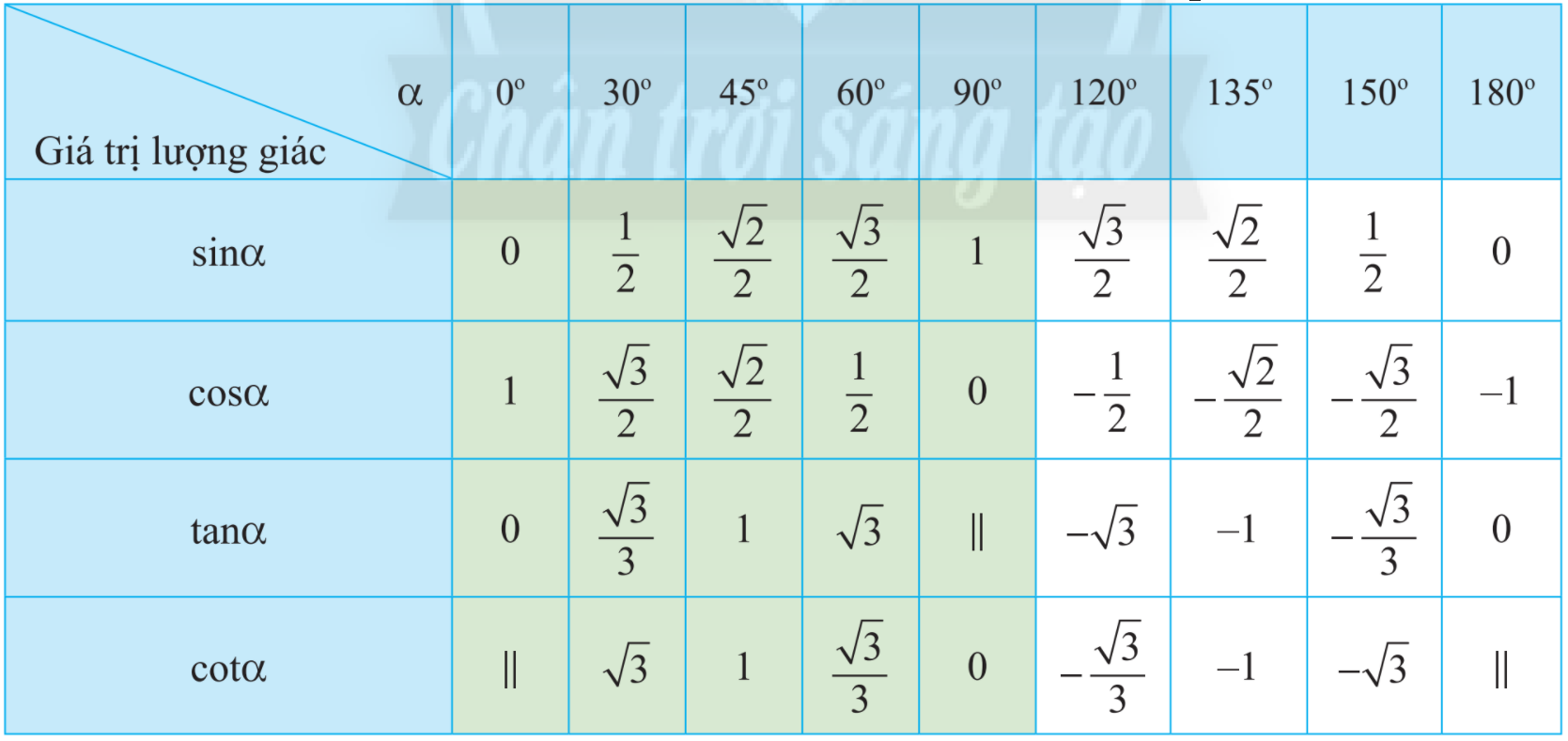
Trả lời:
a) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\cos \alpha \) ta có:
\(\cos \alpha = \frac{{ - \sqrt 2 }}{2}\) với \(\alpha = {135^o}\)
b) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\sin \alpha \) ta có:
\(\sin \alpha = 0\) với \(\alpha = {0^o}\) và \(\alpha = {180^o}\)
c) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\tan \alpha \) ta có:
\(\tan \alpha = 1\) với \(\alpha = {45^o}\)
d) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\cot \alpha \) ta có:
\(\cot \alpha \) không xác định với \(\alpha = {0^o}\) hoặc \(\alpha = {180^o}\)
Câu hỏi:
Cho tam giác ABC. Chứng minh rằng:
a) \(\sin A = \sin \;(B + C)\)
b) \(\cos A = - \cos \;(B + C)\)
Phương pháp:
\(\begin{array}{l}\sin \left( {{{180}^o} - A} \right) = \sin A\\\cos \left( {{{180}^o} - A} \right) = - \cos A\end{array}\)\(({0^o} \le \widehat A \le {180^o})\)
Ta có: \(A+B+C=180^o\)
a)
\(\sin (B + C) = \sin \left( {{{180}^o} - A} \right) = \sin A\)
Vậy \(\sin A = \sin \;(B + C)\)
b)
\(\cos (B + C) = \cos \left( {{{180}^o} - A} \right) = - \cos A\)
Vậy \(\cos A = - \cos \;(B + C)\)
Câu hỏi:
b) \(\tan \alpha .\cot \alpha = 1\;({0^o} < \alpha < {180^o},\alpha \ne {90^o})\)
c) \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\;(\alpha \ne {90^o})\)
d) \(1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\;({0^o} < \alpha < {180^o})\)
Phương pháp:
Lấy điểm M trên nửa đường tròn đơn vị sao cho \(\alpha = \widehat {xOM}\)
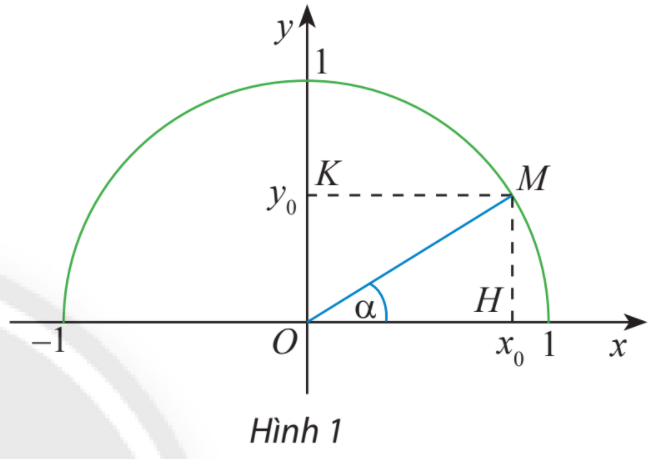
\(\sin \alpha = \frac{{MH}}{{OM}};\;\cos \alpha = \frac{{OH}}{{OM}};\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.\)
Trên nửa đường tròn đơn vị, lấy điểm M sao cho \(\widehat {xOM} = \alpha \)
Gọi H, K lần lượt là các hình chiếu vuông góc của M trên Ox, Oy.
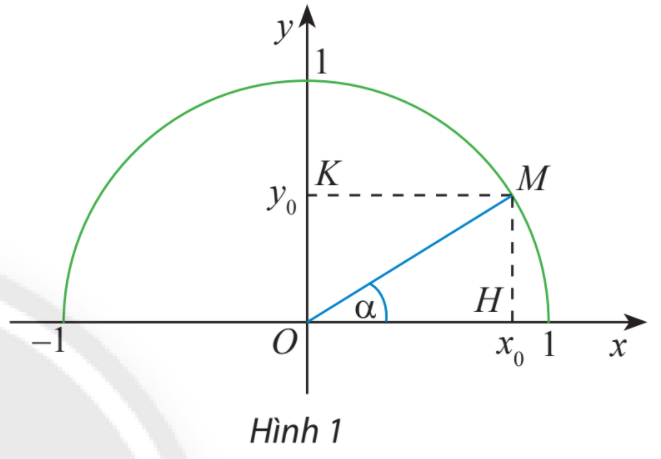
Ta có: tam giác vuông OHM vuông tại H và \(\alpha = \widehat {xOM}\)
Do đó: \(\sin \alpha = \frac{{MH}}{{OM}} = MH;\;\cos \alpha = \frac{{OH}}{{OM}} = OH.\)
\( \Rightarrow {\cos ^2}\alpha + {\sin ^2}\alpha = O{H^2} + M{H^2} = O{M^2} = 1\)
Ta có:
\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.\\ \Rightarrow \;\tan \alpha .\cot \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\end{array}\)
Với \(\alpha \ne {90^o}\) ta có:
\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\\ \Rightarrow \;1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\;\end{array}\)
Ta có:
\(\begin{array}{l}\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }};\;\\ \Rightarrow \;1 + {\cot ^2}\alpha = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\;\end{array}\)
Câu hỏi:
Cho góc \(\alpha \) với \(\cos \alpha = - \frac{{\sqrt 2 }}{2}.\) Tính giá trị của biểu thức \(A = 2{\sin ^2}\alpha + 5{\cos ^2}\alpha .\)
Phương pháp:
Sử dụng đẳng thức \({\cos ^2}\alpha + {\sin ^2}\alpha = 1\)
Trả lời:
Ta có: \(A = 2{\sin ^2}\alpha + 5{\cos ^2}\alpha = 2({\sin ^2}\alpha + {\cos ^2}\alpha ) + 3{\cos ^2}\alpha \)
Mà \({\cos ^2}\alpha + {\sin ^2}\alpha = 1;\cos \alpha = - \frac{{\sqrt 2 }}{2}.\)
\( \Rightarrow A = 2 + 3.{\left( { - \frac{{\sqrt 2 }}{2}} \right)^2} = 2 + 3.\frac{1}{2} = \frac{7}{2}.\)
Câu hỏi:
Dùng máy tính cầm tay, hãy thực hiện các yên cầu dưới đây:
a) Tính \(\sin {168^o}45'33'';\cos {17^o}22'35'';\tan {156^o}26'39'';\cot {56^o}36'42''.\)
b) Tìm \(\alpha \;({0^o} \le \alpha \le {180^o}),\)trong các trường hợp sau:
i) \(\sin \alpha = 0,862.\)
ii) \(\cos \alpha = - 0,567.\)
iii) \(\tan \alpha = 0,334.\)
Phương pháp:
a) Để tính \(\sin {168^o}45'33''\), bấm liên tiếp các phím:

Để tính \(\cot {56^o}36'42''\) ta tính \(1:\tan {56^o}36'42''\).
b) Để tìm \(\alpha \) biết \(\sin \alpha = 0,862\), bấm liên tiếp các phím:

Trả lời:
a)
\(\begin{array}{l}\sin {168^o}45'33'' = 0,195;\\\cos {17^o}22'35'' = 0,954;\\\tan {156^o}26'39'' = - 0,436;\\\cot {56^o}36'42'' = 0,659\end{array}\)
b)
i) \(\alpha = {59^o}32'30,8''.\)
ii) \(\alpha = {124^o}32'28,65''.\)
iii) \(\alpha = {18^o}28'9,55''.\)
Giải bài tập Toán 10 trang 72, 73 Chân trời sáng tạo tập 1 - Bài 2: Định lí côsin và định lí sin. Bài 1 : Tính độ dài cạnh x trong các tam giác sau :
Giải bài tập Toán 10 trang 77, 78 Chân trời sáng tạo tập 1 - Bài 3: Giải tam giác và ứng dụng thực tế. Bài 1 : Giải tam giác ABC trong các trường hợp sau:
Giải bài tập Toán 10 trang 78, 79 Chân trời sáng tạo tập 1 - Bài tập cuối chương 4. Bài 5 : Cho hình bình hành ABCD. a) Chứng minh 2(AB2 + BC2) = AC2 + BD2.
Giải bài tập Toán 10 trang 86, 87 Chân trời sáng tạo tập 1 - Bài 1: Khái niệm vectơ. Bài 1: a) Bạn hãy tìm sự khác biệt giữa hai đại lượng sau: - Bác Ba có số tiền là 20 triệu đồng. - Một cơn bão di chuyển với vận tốc 20 km/h theo hướng đông bắc.
