A. Trắc nghiệm

Bài 6.36 trang 25 SGK Toán 8 Kết nối tri thức tập 2

Khẳng định nào sau đây là đúng:

A. \(\frac{{{{\left( {x - 1} \right)}^2}}}{{x - 2}} = \frac{{{{\left( {1 - x} \right)}^2}}}{{2 - x}}\)

B. \(\frac{{3{\rm{x}}}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{3{\rm{x}}}}{{{{\left( {x - 2} \right)}^2}}}\)

C. \(\frac{{3{\rm{x}}}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{ - 3{\rm{x}}}}{{{{\left( {x - 2} \right)}^2}}}\)

D. \(\frac{{3{\rm{x}}}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{3{\rm{x}}}}{{{{\left( { - x - 2} \right)}^2}}}\)\(\)

Lời giải:

Khẳng định D là khẳng định đúng

Vì \({\left( {x + 2} \right)^2} = {\left( { - x - 2} \right)^2}\)

Bài 6.37 trang 25 SGK Toán 8 Kết nối tri thức tập 2

Khẳng định nào sau đây là sai:

A. \(\frac{{ - 6{\rm{x}}}}{{ - 4{{\rm{x}}^2}{{\left( {x + 2} \right)}^2}}} = \frac{3}{{2{\rm{x}}{{\left( {x + 2} \right)}^2}}}\)

B. \(\frac{{ - 5}}{{ - 2}} = \frac{{10{\rm{x}}}}{{4{\rm{x}}}}\)

C. \(\frac{{x + 1}}{{x - 1}} = \frac{{{x^2} + x + 1}}{{{x^2} - x + 1}}\)

D. \(\frac{{ - 6{\rm{x}}}}{{ - 4{{\left( { - x} \right)}^2}{{\left( {x - 2} \right)}^2}}} = \frac{3}{{2{\rm{x}}{{\left( { - x + 2} \right)}^2}}}\)

Lời giải:

Đáp án đúng là: C

Khẳng định C là sai vì:

(x + 1)(x² – x + 1) = x³ + 1 và (x – 1)(x² + x + 1) = x³ – 1.

Suy ra (x + 1)(x² – x + 1) ≠ (x – 1)(x² + x + 1).

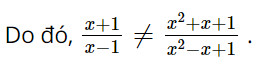
Bài 6.38 trang 25 SGK Toán 8 Kết nối tri thức tập 2

Trong hằng đẳng thức \(\frac{{2{{\rm{x}}^2} + 1}}{{4{\rm{x}} - 1}} = \frac{{8{{\rm{x}}^3} + 4{\rm{x}}}}{Q}\), Q là đa thức

A.4x

B. \(4{{\rm{x}}^2}\)

C.16x−4

D. \(16{{\rm{x}}^2} - 4{\rm{x}}\)

Lời giải:

\(\begin{array}{l}\frac{{2{{\rm{x}}^2} + 1}}{{4{\rm{x}} - 1}} = \frac{{8{{\rm{x}}^3} + 4{\rm{x}}}}{Q}\\ \Rightarrow Q = \frac{{\left( {8{{\rm{x}}^3} + 4{\rm{x}}} \right)\left( {4{\rm{x}} - 1} \right)}}{{2{{\rm{x}}^2} + 1}}\\Q = \frac{{4{\rm{x}}\left( {2{{\rm{x}}^2} + 1} \right)\left( {4{\rm{x}} - 1} \right)}}{{2{{\rm{x}}^2} + 1}}\\Q = 4{\rm{x}}\left( {4{\rm{x}} - 1} \right) = 16{{\rm{x}}^2} - 4{\rm{x}}\end{array}\)

Đáp án D

Bài 6.39 trang 25 SGK Toán 8 Kết nối tri thức tập 2

Nếu \(\frac{{ - 5{\rm{x}} + 5}}{{2{\rm{x}}y}} - \frac{{ - 9{\rm{x}} - 7}}{{2{\rm{x}}y}} = \frac{{b{\rm{x}} + c}}{{xy}}\) thì b + c

A. -4

B. 8

C. 4

D. -10

Lời giải:

Đáp án đúng là: B

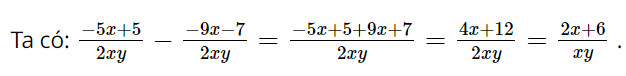
Suy ra b = 2 và c = 6.

Vậy b + c = 2 + 6 = 8.

Bài 6.40 trang 25 SGK Toán 8 Kết nối tri thức tập 2

Một ngân hàng huy động vốn với mức lãi suất một năm là x%. Để sau một năm, người gửi lãi a đồng thì người đó phải gửi vào ngân hàng số tiền là:

A. \(\frac{{100{\rm{a}}}}{x}\) (đồng)

B. \(\frac{a}{{x + 100}}\) (đồng)

C. \(\frac{a}{{x + 1}}\) (đồng)

D. \(\frac{{100{\rm{a}}}}{{x + 100}}\) (đồng)

Lời giải:

Sau một năm, người gửi lãi a đồng thì người đó phải gửi vào ngân hàng số tiền là: \(\frac{{100{\rm{a}}}}{x}\)

Chọn đáp án A

B. Tự luận

Bài 6.41 trang 26 SGK Toán 8 Kết nối tri thức tập 2

Tìm đa thức P trong các đẳng thức sau:

a) \(P + \frac{1}{{x + 2}} = \frac{x}{{{x^2} - 2{\rm{x}} + 4}}\)

b) \(P - \frac{{4\left( {x - 2} \right)}}{{x + 2}} = \frac{{16}}{{x - 2}}\)

c) \(P.\frac{{x - 2}}{{x + 3}} = \frac{{{x^2} - 4{\rm{x}} + 4}}{{{x^2} - 9}}\)

d) \(P:\frac{{{x^2} - 9}}{{2{\rm{x}} + 4}} = \frac{{{x^2} - 4}}{{{x^2} + 3{\rm{x}}}}\)

Lời giải:

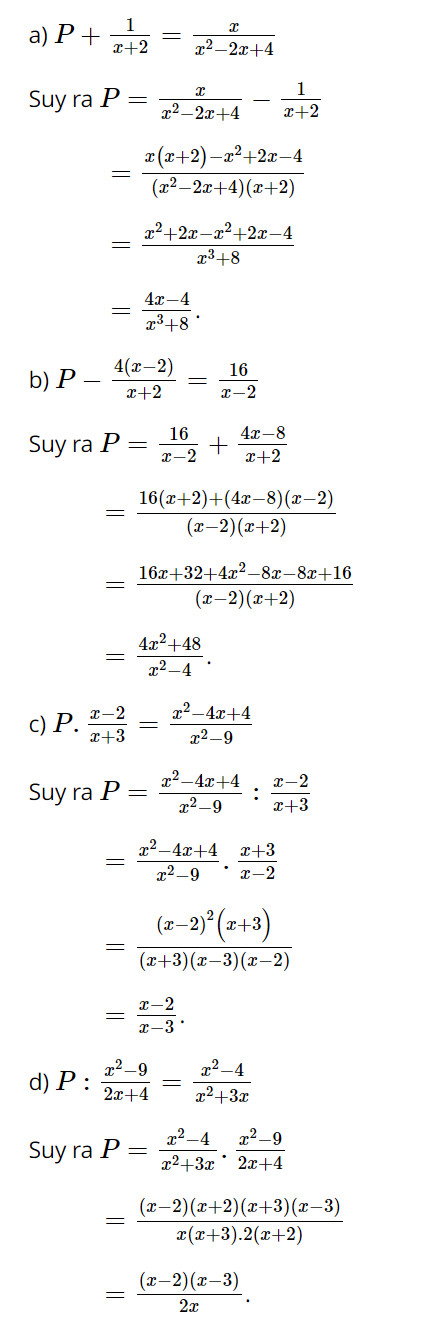
Bài 6.42 trang 26 SGK Toán 8 Kết nối tri thức tập 2

Rút gọn biểu thức sau:

a) \(\frac{2}{{3{\rm{x}}}} + \frac{x}{{x - 1}} + \frac{{6{{\rm{x}}^2} - 4}}{{2{\rm{x}}\left( {1 - x} \right)}}\)

b) \(\frac{{{x^3} + 1}}{{1 - {x^3}}} + \frac{x}{{x - 1}} - \frac{{x + 1}}{{{x^2} + x + 1}}\)

c) \(\left( {\frac{2}{{x + 2}} - \frac{2}{{1 - x}}} \right).\frac{{{x^2} - 4}}{{4{{\rm{x}}^2} - 1}}\)

d) \(1 + \frac{{{x^3} - x}}{{{x^2} + 1}}\left( {\frac{1}{{1 - x}} - \frac{1}{{1 - {x^2}}}} \right)\)

Lời giải:

a)

a) \(\frac{2}{{3{\rm{x}}}} + \frac{x}{{x - 1}} + \frac{{6{x^2} - 4}}{{2x\left( {1 - x} \right)}}\)\( = \frac{2}{{3{\rm{x}}}} + \frac{{ - x}}{{1 - x}} + \frac{{3{{\rm{x}}^2} - 2}}{{x\left( {1 - x} \right)}}\)\( = \frac{{2 - 2x - 3{x^2} + 9{x^2} - 6}}{{3x\left( {1 - x} \right)}}\)

\( = \frac{{6{x^2} - 2x - 4}}{{3x\left( {1 - x} \right)}} = \frac{2({3x+1})}{3x} \)

b)

\(\begin{array}{l}\frac{{{x^3} + 1}}{{1 - {x^3}}} + \frac{x}{{x - 1}} - \frac{{x + 1}}{{{x^2} + x + 1}}\\ = \frac{{ - {x^3} - 1}}{{{x^3} - 1}} + \frac{x}{{x - 1}} - \frac{{x + 1}}{{{x^2} + x + 1}}\\ = \frac{{ - {x^3} - 1 + x\left( {{x^2} + x + 1} \right) - \left( {{x^2} - 1} \right)}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}\\ = \frac{{ - {x^3} - 1 + {x^3} + {x^2} + x - {x^2} + 1}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}\\ = \frac{x}{{{x^3} - 1}}\end{array}\)

c)

Ta có: \(\frac{2}{{x + 2}} - \frac{2}{{1 - x}} = \frac{{2\left( {1 - x} \right) - 2\left( {x + 2} \right)}}{{\left( {x + 2} \right)\left( {1 - x} \right)}} = \frac{{2 - 2{\rm{x}} - 2{\rm{x}} - 4}}{{\left( {x + 2} \right)\left( {1 - x} \right)}} = \frac{{ - 4x - 2}}{{\left( {x + 2} \right)\left( {1 - x} \right)}} = \frac{{2\left( {2x + 1} \right)}}{{\left( {x + 2} \right)\left( {x - 1} \right)}}\);

\(\frac{{{x^2} - 4}}{{4{{\rm{x}}^2} - 1}} = \frac{{\left( {x - 2} \right)\left( {x + 2} \right)}}{{\left( {2x - 1} \right)\left( {2x + 1} \right)}}\).

Do đó

 \(\begin{array}{l}\left( {\frac{2}{{x + 2}} - \frac{2}{{1 - x}}} \right).\frac{{{x^2} - 4}}{{4{{\rm{x}}^2} - 1}} = \frac{{2\left( {2x + 1} \right)}}{{\left( {x + 2} \right)\left( {x - 1} \right)}}.\frac{{\left( {x - 2} \right)\left( {x + 2} \right)}}{{\left( {2x - 1} \right)\left( {2x + 1} \right)}}\\ = \frac{{2(x - 2)}}{{\left( {2x - 1} \right)\left( {x - 1} \right)}}\end{array}\)

d)

\(\begin{array}{l}1 + \frac{{{x^3} - x}}{{{x^2} + 1}}\left( {\frac{1}{{1 - x}} - \frac{1}{{1 - {x^2}}}} \right)\\ = 1 + \frac{{{x^3} - x}}{{{x^2} + 1}}\left( {\frac{1}{{1 - x}} - \frac{1}{{1 - {x^2}}}} \right)\\ = 1 + \frac{{{x^3} - x}}{{{x^2} + 1}}.\frac{{1 + x - 1}}{{1 - {x^2}}}\\ = 1 + \frac{{x\left( {{x^2} - 1} \right)}}{{{x^2} + 1}}.\frac{x}{{1 - {x^2}}}\\ = 1 + \frac{{ - {x^2}\left( {{x^2} - 1} \right)}}{{\left( {{x^2} + 1} \right)\left( {{x^2} - 1} \right)}}\\ = 1 + \frac{{ - {x^2}}}{{{x^2} + 1}}\\ = \frac{{{x^2} + 1 - {x^2}}}{{{x^2} + 1}}\\ = \frac{1}{{{x^2} + 1}}\end{array}\)

Bài 6.43 trang 26 SGK Toán 8 Kết nối tri thức tập 2

Cho phân thức: \(P = \frac{{2{\rm{x}} + 1}}{{x + 1}}\)

a) Viết điều kiện xác định của P

b) Hãy viết P dưới dạng \(a - \frac{b}{{x + 1}}\), trong đó a, b là số nguyên dương

c) Với giá trị nào của x thì P có giá trị là số nguyên

Lời giải:

a) Điều kiện xác định của P là x + 1 ≠ 0 hay x ≠ –1.

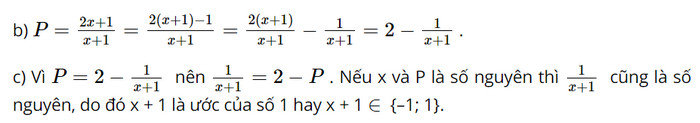
Do vậy x + 1 = – 1, suy ra x = – 2 hoặc x + 1 = 1, suy ra x = 0.

Vậy giá trị của P là số nguyên khi x = 0 hoặc x = – 2.

Bài 6.44 trang 26 SGK Toán 8 Kết nối tri thức tập 2

Một xe ô tô đi từ Hà Nội đến Vinh với vận tốc 60km/h và dự kiến sẽ đến Vinh sau 5 giờ chạy. Tuy nhiên, sau \(2\frac{2}{3}\) giờ chạy với vận tốc 60km/h, xe dừng nghỉ 20 phút. Sau khi dừng nghỉ, để đến Vinh đúng thời gian dự kiến, xe phải tăng vận tốc so với chặng đầu

a) Tính độ dài quãng đường Hà Nội - Vinh

b) Tính độ dài quãng đường còn lại sau khi dừng nghỉ

c) Cho biết ở chặng thứ hai xe tăng vận tốc thêm x (km/h). Hãy viết biểu thức P biểu thị thời gian (tính bằng giờ) thực tế xe chạy hết chặng đường Hà Nội - Vinh

d) Tính thời gian của P lần lượt tại x = 5, x = 10; x = 15, từ đó cho biết ở chặng thứ hai (sau khi xe dừng nghỉ):

- Nếu tăng vận tốc thêm 5km/h thì xe đến Vinh muộn hơn dự kiến bao nhiêu giờ?

- Nếu tăng vận tốc thêm 10km/h thì xe đến Vinh có đúng thời gian dự kiến không?

- Nếu tăng vận tốc thêm 15km/h thì xe đến Vinh sớm hơn dự kiến bao nhiêu giờ? 

Lời giải:

a) Độ dài quãng đường Hà Nội - Vinh: s = v.t => s = 60.5 = 300 (km)

b) Độ dài quãng đường còn lại sau khi dừng nghỉ: 300 − (60. \(\frac{8}{3}\)) = 140 (km)

c)  \(P = \frac{8}{3} + \frac{{140}}{{x + 60}} + \frac{1}{3} = 3 + \frac{{140}}{{x + 60}}\)

d) Có x = 5 => \(P = \frac{{67}}{{13}}\)

         x = 10 => P = 5

        x = 15 => P = \(\frac{{73}}{{15}}\)

=> Nếu tăng vận tốc thêm 5km/h thì xe đến Vinh muộn hơn dự kiến \(\frac{2}{{13}}\) giờ

 Nếu tăng vận tốc thêm 10km/h thì xe đến Vinh đến đúng thời gian dự kiến

 Nếu tăng vận tốc thêm 15km/h thì xe đến Vinh sớm hơn dự kiến \(\frac{2}{{15}}\) giờ

Giaibaitap.me