Bài 1 trang 22 SGK Toán 8 Chân trời sáng tạo tập 2

Tìm các hàm số bậc nhất trong các hàm số sau đây và xác định các hệ số \(a,b\) của chúng.

a) \(y = 4x + 2\);                  b) \(y = 5 - 3x\);                            c) \(y = 2 + {x^2}\);

d) \(y =  - 0,2x\);                  e) \(y = \sqrt 5 x - 1\).

Lời giải:

a) Hàm số \(y = 4x + 2\) là hàm số bậc nhất vì có dạng \(y = ax + b\) với\(a,b\) là các số cho trước và \(a \ne 0\). Ta có, \(a = 4;b = 2\).

b) Hàm số \(y = 5 - 3x =  - 3x + 5\) là hàm số bậc nhất vì có dạng \(y = ax + b\) với\(a,b\) là các số cho trước và \(a \ne 0\). Ta có, \(a =  - 3;b = 5\).

c) Hàm số \(y = 2 + {x^2}\) không phải là hàm số bậc nhất vì không có dạng \(y = ax + b\) với\(a,b\) là các số cho trước và \(a \ne 0\).

d) Hàm số \(y =  - 0,2x\) là hàm số bậc nhất vì có dạng \(y = ax + b\) với\(a,b\) là các số cho trước và \(a \ne 0\). Ta có, \(a =  - 0,2;b = 0\).

e) Hàm số \(y = \sqrt 5 x - 1\) là hàm số bậc nhất vì có dạng \(y = ax + b\) với\(a,b\) là các số cho trước và \(a \ne 0\). Ta có, \(a = \sqrt 5 ;b =  - 1\).

Bài 2 trang 22 SGK Toán 8 Chân trời sáng tạo tập 2

Với giá trị nào của \(m\) thì mỗi hàm số sau đây là hàm số bậc nhất?

a) \(y = \left( {m - 1} \right)x + m\);                        b) \(y = 3 - 2mx\).

Lời giải:

a) Điều kiện để hàm số y = (m − 1)x + m là hàm số bậc nhất là m − 1 ≠ 0 hay m ≠ 1.

b) Điều kiện để hàm số y = 3 − 2mx là hàm số bậc nhất là −2m ≠ 0 hay m ≠ 0.

Bài 3 trang 22 SGK Toán 8 Chân trời sáng tạo tập 2

a) Vẽ đồ thị các hàm số sau đây trên cùng một mặt phẳng tọa độ:

\(y = x\);        \(y = x + 2\);              \(y =  - x\)                 \(y =  - x + 2\).

b) Bốn đồ thị nói trên cắt nhau tại các điểm \(O\left( {0;0} \right),A,B,C\). Tứ giác có bốn đỉnh \(O;A;B;C\) là hình gì? Giải thích.

Lời giải:

a) 

- Vẽ đồ thị hàm số \(y = x\)

Cho \(x = 1 \Rightarrow y = 1\)\( \Rightarrow \) đồ thị hàm số đi qua điểm \(A\left( {1;1} \right)\).

Đồ thị hàm số \(y = x\)là đường thẳng đi qua hai điểm \(O\left( {0;0} \right)\) và \(A\left( {1;1} \right)\).

- Vẽ đồ thị hàm số \(y = x + 2\)

Cho \(x = 0 \Rightarrow y = 2\) ta được điểm \(B\left( {0;2} \right)\) trên trục \(Oy\).

Cho \(y = 0 \Rightarrow x =  - 2\) ta được điểm \(M\left( { - 2;0} \right)\) trên \(Ox\).

Đồ thị hàm số\(y = x + 2\)là đường thẳng đi qua hai điểm \(B\left( {0;2} \right)\) và \(M\left( { - 2;0} \right)\).

- Vẽ đồ thị hàm số \(y =  - x\)

Cho \(x = 1 \Rightarrow y =  - 1\)\( \Rightarrow \) đồ thị hàm số đi qua điểm \(C\left( {1; - 1} \right)\).

Đồ thị hàm số \(y =  - x\) là đường thẳng đi qua hai điểm \(O\left( {0;0} \right)\) và \(C\left( {1; - 1} \right)\).

- Vẽ đồ thị hàm số \(y =  - x + 2\)

Cho \(x = 0 \Rightarrow y = 2\) ta được điểm \(B\left( {0;2} \right)\) trên trục \(Oy\).

Cho \(y = 0 \Rightarrow x = 2\) ta được điểm \(N\left( {2;0} \right)\) trên \(Ox\).

Đồ thị hàm số \(y =  - x + 2\) là đường thẳng đi qua hai điểm \(B\left( {0;2} \right)\) và \(N\left( {2;0} \right)\).

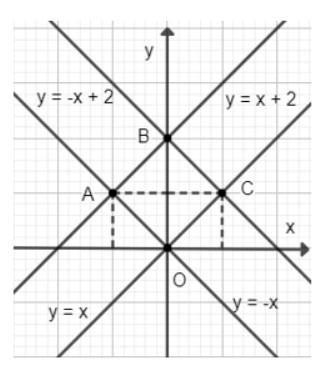
b) 

Vì đường thẳng \(y = x\);\(y = x + 2\) song song với nhau và \(y =  - x\);\(y =  - x + 2\) song song với nhau nên tứ giác \(OABC\) là hình bình hành.

Lại có \(OC;OA\) là đường chéo của hình vuông có độ dài cạnh là 1 nên \(OC = OA\). Do đó, tứ giác \(OABC\) là hình thoi.

Lại có \(OC;OA\) là đường chéo của hình vuông nên cũng là đường phân giác. Do đó, \(\widehat {COB} = \widehat {AOB} = 45^\circ  \Rightarrow \widehat {COA} = \widehat {COB} + \widehat {AOB} = 45^\circ  + 45^\circ  = 90^\circ \)

Hình thoi \(OABC\) có góc \(\widehat {COA} = 90^\circ \) nên tứ giác \(OABC\) là hình vuông.

Bài 4 trang 22 SGK Toán 8 Chân trời sáng tạo tập 2

Để đổi nhiệt độ từ \(F\) (Fahrenheit) sang độ \(C\) (Celsius), ta dùng công thức \(C = \dfrac{5}{9}.\left( {F - 32} \right)\).

a) \(C\) có phải hàm số bậc nhất theo biến số \(F\) không?

b) Hãy tính \(C\) khi \(F = 32\) và tính \(F\) khi \(C = 100\).

Lời giải:

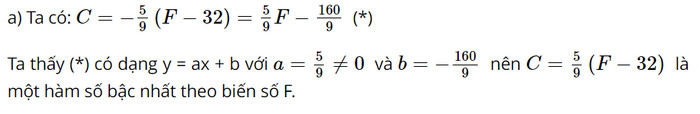
b) Khi F = 32 ta có:

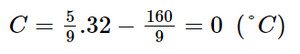
Khi C = 100, thế vào (*) ta có:

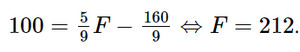
Bài 5 trang 22 SGK Toán 8 Chân trời sáng tạo tập 2

Gọi \(C\) và \(r\) lần lượt là chu vi và bán kính của một đường tròn. Hãy chứng tỏ \(C\) là một hàm số bậc nhất theo biến số \(r\). Tìm hệ số \(a,b\) của hàm số này.

Lời giải:

Công thức tính chu vi đường tròn:

\(C = \pi .d = \pi .2r\) (đơn vị độ dài)

Trong đó, \(C\) là chu vi đường tròn; \(r\) là bán kính đường tròn; \(d\) là đường kính đường tròn.

Vì \(C = 2\pi .r\) nên \(C\) là hàm số bậc nhất theo biến \(r\) vì có dạng \(C = a.r + b\).

Ta có: \(C = 2\pi .r\) nên \(a = 2\pi ;b = 0\).

Vậy C là một hàm số bậc nhất theo biến \(r\) với \(a = 2\pi ;b = 0\).

Bài 6 trang 22 SGK Toán 8 Chân trời sáng tạo tập 2

Một người đi bộ trên đường thẳng với tốc độ \(v\left( {km/h} \right)\). Gọi \(s\left( {km} \right)\) là quãng đường đi được trong \(t\left( h \right)\). 

a) Lập công thức tính \(s\) theo \(t\).

b) Vẽ đồ thị của hàm số \(s\) theo \(t\) khi \(v = 4\).

Lời giải:

a) s = vt.

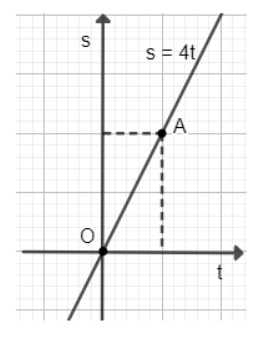
b) Hàm số: s = 4t.

Đồ thị hàm số s = 4t là đường thẳng đi qua 2 điểm O(0; 0); A(1; 4).

Giaibaitap.me