Bài 1 trang 26 SGK Toán 8 Chân trời sáng tạo tập 2

Cho hàm số bậc nhất \(y = ax - 4\)

a) Tìm hệ số góc \(a\) biết rằng đồ thị hàm số đi qua điểm \(M\left( {1; - 2} \right)\).

b) Vẽ đồ thị của hàm số.

Lời giải:

a) Đồ thị hàm số đi qua điểm M(1; −2) nên ta có: −2 = a − 4 suy ra a = 2.

b) Đồ thi hàm số y = 2x − 4 đi qua hai điểm A(0; −4) và B(2; 0).

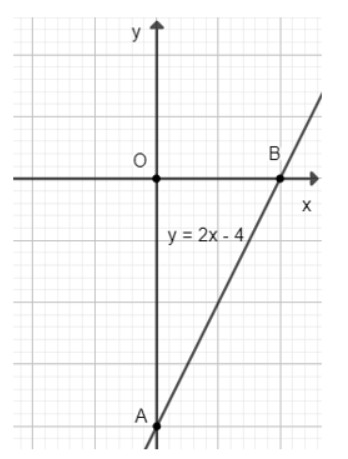
Bài 2 trang 26 SGK Toán 8 Chân trời sáng tạo tập 2

a) Vẽ đồ thị của hàm số \(y = x\) và \(y = x + 2\) trên cùng một mặt phẳng tọa độ.

b) Dùng thước đo góc để tìm góc tạo bởi hai đường thẳng  \(y = x\) và \(y = x + 2\) với trục \(Ox\).

Lời giải:

a)

- Vẽ đồ thị hàm số \(y = x\).

Cho \(x = 1 \Rightarrow y = 1 \Rightarrow \)Đồ thị hàm số đi qua điểm \(M\left( {1;1} \right)\).

Đồ thị hàm số \(y = x\) là đường thẳng đi qua hai điểm \(O\) và \(M\).

- Vẽ đồ thị hàm số \(y = x + 2\)

Cho \(x = 0 \Rightarrow y = 2\) ta được điểm \(A\left( {0;2} \right)\) trên trục \(Oy\).

Cho \(y = 0 \Rightarrow x = \dfrac{{ - 2}}{1} =  - 2\) ta được điểm \(B\left( { - 2;0} \right)\) trên \(Ox\).

Đồ thị hàm số \(y = x + 2\) là đường thẳng đi qua hai điểm \(A\) và \(B\). 

b) Góc tạo bởi hai đường thẳng  \(y = x\) và \(y = x + 2\) với trục \(Ox\) lần lượt là \({\alpha _1}\) và \({\alpha _2}\).

Dùng thước đo độ kiểm tra ta thấy số đo \({\alpha _1} = {\alpha _2} = 45^\circ \).

Bài 3 trang 26 SGK Toán 8 Chân trời sáng tạo tập 2

Hãy chỉ ra ba cặp đường thẳng cắt nhau và các cặp đường thẳng song song với nhau trong các đường thẳng sau:

\({d_1}:y = 0,2x\);          \({d_2}:y =  - 2x + 4\);                       \({d_3}:y = 0,2x - 0,8\);

\({d_4}:y =  - 2x - 5\);               \({d_5}:y = \sqrt 3 x + 3\);                           \({d_6}:y = \sqrt 3 x - \sqrt 5 \). 

Lời giải:

Ba cặp đường thẳng cắt nhau: d₁ và d₂; d₂ và d₃; d₃ và d₄ (vì hai đường thẳng trong mỗi cặp có hệ số góc khác nhau).

Các cặp đường thẳng song song: d₁ và d₃ (có hế số góc đều bằng 0,2), d₂ và d₄ ( có hệ số góc đều bằng −2); d₅ và d₆ ( có hệ số góc đều bằng ).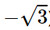

Bài 4 trang 26 SGK Toán 8 Chân trời sáng tạo tập 2

Tìm hệ số góc \(a\) để hai đường thẳng \(y = ax + 2\) và \(y = 9x - 9\) song song với nhau.

Lời giải:

Để hai đường thẳng \(y = ax + 2\) và \(y = 9x - 9\) song song với nhau thì \(\left\{ \begin{array}{l}a = 9\\2 \ne  - 9\end{array} \right. \Rightarrow a = 9\).

Do đó, để đường thẳng \(y = ax + 2\) song song với đường thẳng \(y = 9x - 9\) thì \(a = 9\).

Bài 5 trang 26 SGK Toán 8 Chân trời sáng tạo tập 2

Cho hai hàm số bậc nhất \(y = 2mx - 5\) và \(y = 2x + 1\).

Với giá trị nào của \(m\) thì đồ thị của hai hàm số đã cho là:

a) Hai đường thẳng song song với nhau?

b) Hai đường thẳng cắt nhau?

Lời giải:

a) Hai đường thẳng y = 2mx – 5 và y = 2x + 1 song song với nhau nên có hệ số góc bằng nhau suy ra m = 1.

b) Hai đường thẳng y = 2mx – 5 và y = 2x + 1 song song với nhau nên có hệ số góc khác nhau suy ra m ≠ 1.

Bài 6 trang 26 SGK Toán 8 Chân trời sáng tạo tập 2

Cho đường thẳng \(d:y = x + 2023\). Xác định hai hàm số biết đồ thị của chúng là hai đường thẳng song song với \(d\).

Lời giải:

Đường thẳng \(d:y = x + 2023\) có \(a = 1;b = 2023\).

- Gọi \({d_1}:y = {a_1}x + {b_1}\) là đường thẳng cần tìm thứ nhất. Vì \({d_1}\) song song với \(d\) nên \(\left\{ \begin{array}{l}a = {a_1}\\b \ne {b_1}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}1 = {a_1}\\2023 \ne {b_1}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{a_1} = 1\\{b_1} \ne 2023\end{array} \right.\). Ta chọn \({b_1} = 25\)

Ta có đường thẳng \({d_1}:y = x + 25\).

Vậy hàm số thứ nhất cần tìm là \(y = x + 25\)

- Gọi \({d_2}:y = {a_2}x + {b_2}\) là đường thẳng cần tìm thứ hai. Vì \({d_2}\) song song với \(d\) nên \(\left\{ \begin{array}{l}a = {a_2}\\b \ne {b_2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}1 = {a_2}\\2023 \ne {b_2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{a_2} = 1\\{b_2} \ne 2023\end{array} \right.\). Ta chọn \({b_2} = 5\)

Ta có đường thẳng \({d_2}:y = x + 5\).

Vậy hàm số thứ hai cần tìm là \(y = x + 5\). 

Bài 7 trang 26 SGK Toán 8 Chân trời sáng tạo tập 2

Cho đường thẳng \(d:y =  - x - 2022\). Xác định hai hàm số biết đồ thị của chúng là hai đường thẳng cắt \(d\).

Lời giải:

Đường thẳng cắt d: y = −x − 2022 suy ra có hệ số góc khác −1.

Ta có:

d’: y = x + 1; d’’: y = 2x + 2022.

Bài 8 trang 27 SGK Toán 8 Chân trời sáng tạo tập 2

Lam phụ giúp mẹ bánh nước chanh, em nhận thấy số ly nước chanh \(y\) bán được trong ngày và nhiệt độ trung bình \(x\left( {^\circ C} \right)\) của ngày hôm đó có mối tương quan. Lan ghi lại các giá trị tương ứng của hai đại lượng \(x\) và \(y\) trong bảng sau:

a) So sánh các giá trị \(x\) và \(y\) tương ứng trong bảng dữ liệu trên với tọa độ \(\left( {x;y} \right)\) của các điểm \(A;B;C;D;E;F\) trên mặt phẳng tọa độ trong Hình 6.

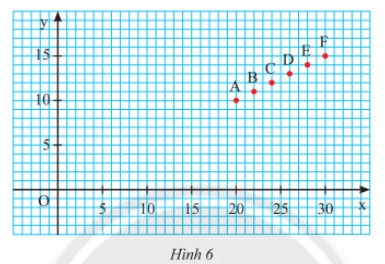
b) Cho biết đường thẳng \(d:y = mx\) đi qua các điểm \(A;B;C;D;E;F\) ở câu a. Tìm hệ số góc của \(d\).

Lời giải:

a) Điểm \(A\left( {20;10} \right);B\left( {22;11} \right);C\left( {24;12} \right);D\left( {26;13} \right);E\left( {28;14} \right);D\left( {30;15} \right)\)

Ta thấy mỗi cặp giá trị \(x;y\) tương ứng trong bảng là tọa độ của các điểm \(A;B;C;D;E;F\). 

b) Vì đường thẳng \(d:y = mx\) đi qua các điểm \(A;B;C;D;E;F\) nên ta chọn \(A\left( {20;10} \right)\) thay vào đường thẳng ta được:

\(10 = 20.m \Leftrightarrow m = 10:20 \Leftrightarrow m = \dfrac{1}{2}\)

Do đó đường thẳng cần tìm là: \(y = \dfrac{1}{2}x\).

Hệ số góc của đường thẳng là \(a = \dfrac{1}{2}\).

Bài 9 trang 27 SGK Toán 8 Chân trời sáng tạo tập 2

Một xe khách khởi hành từ bến xe phía Nam bưu điện thành phố Huế để đi vào thành phố Quy Nhơn với tốc độ 50 \(km/h\).

a) Cho biết bến xe cách bưu điện thành phố Huế 4 \(km\). Sau \(x\) giờ, xe khách cách bưu điện thành phố Huế \(y\)\(km\). Tính \(y\) theo \(x\).

b) Tìm hệ số góc của đường thẳng là đồ thị của hàm số \(y\) ở câu a.

Lời giải:

a) y = 50x + 4 (km)

b) Hệ số góc a = 50.

Bài 10 trang 27 SGK Toán 8 Chân trời sáng tạo tập 2

Một người bắt đầu mở một vòi nước vào một cái bể đã chứa sẵn 3 \({m^3}\) nước, mỗi giờ chảy được 1 \({m^3}\).

a) Tính thể tích \(y\left( {{m^3}} \right)\) của nước có trong bể sau \(x\) giờ.

b) Vẽ đồ thị của hàm số \(y\) theo biến số \(x\).

Lời giải:

a) Vì mỗi giờ vòi nước chảy được 1 \({m^3}\) nên sau \(x\) giờ vòi đã chảy được \(1.x\) \(\left( {{m^3}} \right)\) nước.

Ban đầu trong bể chứa sẵn 3 \({m^3}\) nước nên lượng nước \(y\) có trong bể sau \(x\) giờ là:

\(y = 1.x + 3 = x + 3\).

b) 

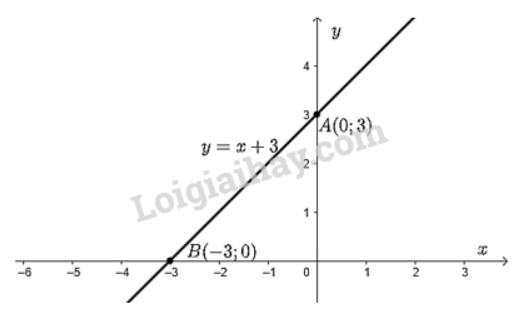
Vẽ đồ thị hàm số \(y = x + 3\)

Cho \(x = 0 \Rightarrow y = 3\) ta được điểm \(A\left( {0;3} \right)\) trên trục \(Oy\).

Cho \(y = 0 \Rightarrow x = \dfrac{{ - 3}}{1} =  - 3\) ta được điểm \(B\left( { - 3;0} \right)\) trên \(Ox\).

Đồ thị hàm số \(y = x + 3\) là đường thẳng đi qua hai điểm \(A;B\).

Giaibaitap.me