Bài 9 trang 26 SGK Hình học 12

Cho hình chóp tứ giác đều $S.ABCD$, đáy là hình vuông cạnh $a$, cạnh bên tạo với đáy một góc $60^0$. Gọi $M$ là trung điểm $SC$. Mặt phẳng đi qua $AM$ và song song với $BD$, cắt $SB$ tại $E$ và cắt $SD$ tại $F$. Tính thể tích khối chóp $S.AEMF$.

Giải

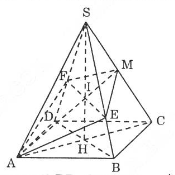
Hình chóp $S.ABCD$ là hình chóp đều nên chân $H$ của đường cao $SH$ chính là tâm của đáy. Mặt phẳng đi qua $AM$ và song song với $BD$ cắt mặt phẳng $(SDB)$ theo một giao tuyến song song với $BD$, hay $EF // BD$. Ta dựng giao tuyến $EF$ như sau: Gọi $I$ là giao điểm của $AM$ và $SH$.

Qua $I$ ta dựng một đường thẳng song song với $BD$, đường này cắt $SB$ ở $E$ và cắt $SD$ ở $F$.

Ta có: $\widehat {SAH}$ = $60^0$. Tam giác cân $SAC$ có $SA = SC$ và góc $SAC = 60^0$ nên nó là tam giác đều: $I$ là giao điểm của các trung tuyến $AM$ và $AH$ nên: ${{SI} \over {SH}} = {2 \over 3}$

Do $EF // DB'$ $\Rightarrow {{{\rm{EF}}} \over {DB}} = {{SF} \over {SD}} = {{SE} \over {SB}} = {{SI} \over {SH}} = {2 \over 3}$

Vì $DB = a\sqrt2$ $\Rightarrow {\rm{EF}} = {{2a\sqrt 2 } \over 3}$

Tam giác $SAC$ là tam giác đều nên $AM = {{AC\sqrt 3 } \over 2} = {{a\sqrt 6 } \over 2}$

Ta lại có $DB \bot (SAC)$ $\Rightarrow DB \bot AM$. Kết hợp với $DB // EF$ nên $EF \bot AM$. Tứ giác $AEMF$ có hai đường chéo vuông góc với nhau nên có diện tích:

${S_{AEMF}} = {1 \over 2}{\rm{EF}}.AM = {1 \over 2}.{{2a\sqrt 2 } \over 3}.{{a\sqrt 6 } \over 2} = {{{a^2}\sqrt 3 } \over 3}$

Mặt khác, tam giác $ASC$ là tam giác đều, $M$ là trung điểm của $SC$ nên $AM \bot SC$. Ta cũng có $DB \bot (SAM)$ $\Rightarrow  DB \bot SC$ vì $DB // EF$ nên $EF \bot SC$. Từ kết quả trên, suy ra $SM \bot(AEMF)$.

Dễ thấy $SM = {{a\sqrt 2 } \over 2}$ (do tam giác $SAC$ đều). Do đó: ${V_{S.AEMF}} = {1 \over 3}.{{{a^2}\sqrt 3 } \over 3}.{{a\sqrt 2 } \over 2} = {{{a^3}\sqrt 6 } \over {18}}$.

Bài 10 trang 27 SGK Hình học 12

Cho hình lăng trụ đứng tam giác $ABC.A'B'C'$ có tất cả các cạnh đều bằng $a$.

a) Tính thể tích khối tứ diện $A'BB'C$.

b) Mặt phẳng đi qua $A'B'$ và trọng tâm tam giác $ABC$, cắt $AC$ và $BC$ lần lượt tại $E$ và $F$. Tính thể tích hình chóp $C.A'B'FE$.

Giải 

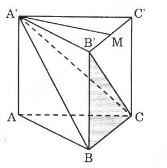
a) Ta tính thể tích hình chóp $A'.BCB'$.

Gọi $M$ là trung điểm của $B'C'$, ta có:

$A'M \bot B'C'$                                (1)

Lăng trụ $ABC.A'B'C'$ là lăng trụ đứng nên:

$BB' \bot (A'B'C')$

$\Rightarrow BB' \bot A'M$                             (2)

Từ (1) và (2) suy ra $A'M \bot (BB'C')$ hay $A'M$ là đường cao của hình chóp $A'.BCB'$.

Ta có: $A'M$ = ${{a\sqrt 3 } \over 2}$ ;        ${S_{BB'C}} = {1 \over 2}{a^2}$

$\Rightarrow {V_{A'BB'C}} = {1 \over 3}.A'M.{S_{BB'C}} \Rightarrow {V_{A'BB'C}} = {{{a^3}\sqrt 3 } \over {12}}$

b) 

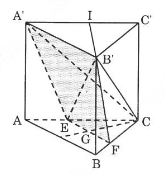
Thể tích hình chóp $C.A'B'EF$ bằng tổng thể tích hai hình chóp:

- $V_1$ là thể tích hình chóp đỉnh $B'$, đáy là tam giác $CEF$.

- $V_2$ là thể tích hình chóp đỉnh $B'$, đáy là tam giác $A'EC$.

Do $(ABC) // (A'B'C')$ nên dễ thấy $EF // AB$. Ta cũng có:

$EF$ = ${2 \over 3}a$

Hình chóp $B'.CEF$ có chiều cao $BB' = a$ và diện tích đáy là:

${S_{C{\rm{EF}}}} = {1 \over 2}.{{2a} \over 3}.{2 \over 3}.{{a\sqrt 3 } \over 2} = {{{a^2}\sqrt 3 } \over 9}$

Từ đây ta có: ${V_1} = {{{a^3}\sqrt 3 } \over {27}}$

Do $EC = {2 \over 3}AC$ nên ${S_{A'EC}} = {2 \over 3}a.{1 \over 2}a = {{{a^2}} \over 3}$

Hình chóp $B'.A'EC$ có chiều cao là $B'I$ (chiều cao của $△A'B'C'$) bằng ${{a\sqrt 3 } \over 2}$ nên $V_2$= ${{{a^3}\sqrt 3 } \over {18}}$

Vậy thể tích hình chóp $C.A'B'FE$ là: $V = V_1 + V_2$ = ${{5{a^3}\sqrt 3 } \over {54}}$

Bài 11 trang 27 SGK Hình học 12

Cho hình hộp $ABCD.A'B'C'D'$. Gọi $E$ và $F$ theo thứ tự là trung điểm của các cạnh $BB'$ và $DD'$. Mặt phẳng $(CEF)$ chia khối hộp trên làm hai khối đa diện. Tính tỉ số thể tích của hai khối đa diện đó.

Giải

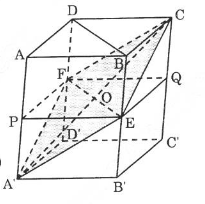
Ta xác định thiết diện của hình hộp $ABCD.A'B'C'D'$ khi cắt bởi $(CEF)$. Mặt phẳng $(CEF)$ chứa đường thẳng $EF$ mà $E$ là trung điểm của $BB', F$ là trung điểm của $CC'$ nên $EF$ chứa giao điểm $O$ của các đường chéo hình hộp, do đó mặt phẳng $(CEF)$ cùng chứa giao điểm $O$ của các đường chéo và nó cũng chứa đường chéo $A'C$ của hình hộp. Ta dễ dàng nhận xét rằng thiết diện chính là hình bình hành $CEA'F$. Qua $EF$ ta dựng một mặt phẳng song song với đáy hình hộp, mặt phẳng này cắt $AA'$ ở $P$ và cắt $CC'$ ở $Q$.

Ta có thể tích của hình hộp $ABCD.PEQF$ là:

$V_{ABCD.PEQF}$= ${1 \over 2}$$V_{ABCD.A'B'C'D'}$    (1)

Chứng minh tương tự ta được:

$V_{CFQE}=V_{A'FPE}$                            (2)

(Hai hình chóp $CFQE$ và $A'FPE$ có chiều cao bằng nhau và diện tích đáy bằng nhau).

Xét khối đa diện $ABCDE'F$ do mặt phẳng $(CEF)$ chia ra trên hình hộp $ABCD.A'B'C'D'$, ta có:

$V_{ABCD.FA'EQ}$ = ${1 \over 2}$ $V_{ABCD.FPE}+V_{A'FPE}$     (3)

Từ (1), (2), (3) suy ra:

$V_{ABCD.FA'EQ}$= ${1 \over 2}$ $V_{ABCD.A'B'C'D'}$  

Vậy mặt phẳng $(CEF)$ chia hình hộp thành hai khối đa diện có thể tích bằng nhau, tỉ số của chúng là $1$.

Chú ý: Có thể lí luận như sau: Giao điểm $O$ của các đường chéo của hình hộp là tâm đối xứng của hình hộp, do đó mặt phẳng $(CEF)$ chứa điểm $O$ nên chia hình hộp thành hai hình đối xứng với nhau qua điểm $O$. Vậy hai hình này là hai hình bằng nhau và có thể tích bằng nhau.

Bài 12 trang 27 SGK Hình học 12

Cho hình lập phương $ABCD.A'B'C'D'$ cạnh $a$. Gọi $M$ là trung điểm của $A'B', N$ là trung điểm của $BC$.

a) Tính thể tích khối tứ diện $ADMN$.

b) Mặt phẳng $(DMN)$ chia khối lập phương đã cho thành hai khối đa diện. Gọi $(H)$ là khối đa diện chứa đỉnh $A, (H')$ là khối đa diện còn lại. Tính tỉ số ${{{V_{(H)}}} \over {{V_{(H')}}}}$.

Giải

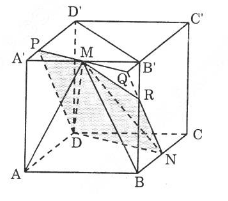
a) Ta tính thể tích hình chóp $M.ADN$. Hình chóp này có chiều cao bằng $a$ và diện tích đáy $AND$ bằng ${{{a^2}} \over 2}$

$V_{ADMN}$ = ${1 \over 3}$ . a . ${{{a^2}} \over 2}$ = ${{{a^3}} \over 6}$

b) Trước hết, ta dựng thiết diện của hình lập phương khi cắt bởi $(DMN)$.

Do $(ABCD) // (A'B'C'D')$ nên $(DMN)$ cắt $(A'B'C'D')$ theo một giao tuyến song song với $DN$. Ta dựng thiết diện như sau:

- Từ $M$ kẻ đường thẳng song song với $DN$, đường này cắt cạnh $A'D'$ tại điểm $P$ và cắt đường thẳng $C'B'$ tại điểm $Q$. Trong mặt phẳng $(BCC'B')$ thì $QN$ cắt cạnh $BB'$ tại điểm $R$; đa giác $DNRMP$  chính là thiết diện của hình lập phương khi cắt bởi $(DMN)$.

- Bây giờ ta tính thể tích khối đa diện $ABNDPMR$. Thể tích này có thể coi là thể tích của ba hình chóp:

          $V_1$ là thể tích hình chóp đáy $ABND$, đỉnh $M$;

          $V_2$  là thể tích hình chóp đáy $AA'PD$, đỉnh $M$;

          $V_3$ là thể tích hình chóp đáy $NRB$, đỉnh $M$.

Hình chóp $M.ABND$, có đường cao bằng $a$, diện tích đáy là hình thang $ABND$ là: 

${1 \over 2}\left( {{a \over 2} + a} \right).a = {{3{a^2}} \over 4}$

Suy ra: ${V_1} = {1 \over 3}.{{3{a^2}} \over 4}.a \Rightarrow {V_1} = {{{a^3}} \over 4}$

 $A'P$ = ${a \over 4}$. Hình chóp $M.AA'PD$ có chiều cao ${a \over 2}$ và diện tích hình thang $AA'PD$ là: ${1 \over 2}\left( {{a \over 4} + a} \right).a = {{5{a^2}} \over 8}$

Suy ra: ${V_2} = {1 \over 3}.{a \over 2}.{{5{a^2}} \over 8} \Rightarrow {V_2} = {{5{a^2}} \over {48}}$

$BR$ = ${2 \over 3}a$. Diện tích tam giác $NRB$ là: ${1 \over 2}.{2 \over 3}a.{a \over 2} = {{{a^2}} \over 6}$

Hình chóp $M.NRB$ có chiều cao ${a \over 2}$ và diện tích đáy ${{{a^2}} \over 6}$ nên:

${V_2} = {1 \over 3}.{a \over 2}.{{{a^2}} \over 6} \Rightarrow {V_3} = {{{a^3}} \over {36}}$

${V_{ABNDPMR}} = {V_1} + {V_2} + {V_3} = {{5{a^3}} \over {48}} + {{{a^3}} \over 4} + {{{a^3}} \over {36}} = {{55{a^3}} \over {144}}$

Thể tích phần còn lại là: ${{144{a^3}} \over {144}} - {{55{a^3}} \over {144}} = {{89{a^3}} \over {144}}$

Từ đây suy ra tỉ số cần tìm là: ${{55} \over {89}}$

Giaibaitap.me