Bài 1 trang 39 sách giáo khoa hình học lớp 12

Cho đường tròn tâm $O$ bán kính $r$ nằm trên mặt phẳng $(P)$. Từ những điểm $M$ thuộc đường tròn này ta kẻ những đường thẳng vuông góc với $(P)$. Chứng minh rằng những đường thẳng như vậy nằm trên một mặt trụ tròn xoay. Hãy xác định trục và bán kính của mặt trụ đó.

Giải

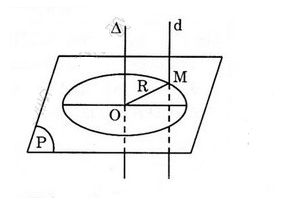
Xét đường thẳng $∆$ đi qua điểm $O$ và vuông góc với mặt phẳng $(P)$. Gọi $d$ là đưởng thẳng đi qua $M\in  (C)$ và $d$ vuông góc với $(P)$. Do đó $d // ∆$. Quay mặt phẳng $(Q)$ tạo bởi $d$ và $∆$ quanh đường thẳng $∆$, thì đường thẳng $d$ vạch lên một mặt trụ tròn xoay. Mặt trụ này chứa tất cả những đường thẳng đi qua các điểm $M \in (C)$ và vuông góc với $(P)$. Trục của mặt trụ là $∆$ và bán kính của trụ bằng $R$.

Trong mỗi trường hợp sau đây, hãy gọi tên các hình tròn xoay hoặc khối tròn xoay sinh ra bởi:

a) Ba cạnh của hình chữ nhật khi quay quanh đường thẳng chứa cạnh thứ tư.

b) Ba cạnh của một tam giác cân khi quay quanh trục đối xứng nó.

c) Một tam giác vuông kể cả các điểm trong của tam giác vuông đó khi quay quanh đường thẳng chứa một cnah góc vuông.

d) Một hình chữ nhật kể cả các điểm trong của hình chữ nhật đó khi quay quanh đường thẳng chứa một cạnh.

Giải:

Theo định nghĩa ta thấy kết quả:

a) Hình trụ tròn xoay có đường cao là cạnh thứ tư còn bán kính hình trụ bằng độ dài của cạnh kề với cạnh thứ tư đó.

b) Hình nón tròn xoay có chiều cao bằng chiều cao của tam giác cân, cond bán kính đáy bằng một nửađộ dài cạnh đáy của tam giác cân đó.

c) Khối nón tròn xoay.

d) Khối trụ tròn xoay.

Bài 3 trang 39 sách giáo khoa hình học lớp 12

Cho hình nón tròn xoay có đường cao $h = 20 cm$, bán kính đáy $r = 25 cm$.

a) Tính diện tích xung quanh của hình nón đã cho.

b) Tính thể tích của khối nón được tạo bởi hình nón đó.

c) Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là $12 cm$. Tính diện tích thiết diện đó.

Giải:

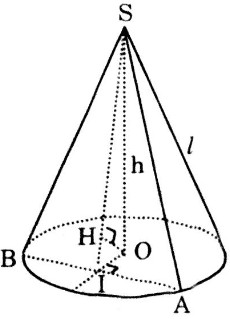
a) Giả sử $SA = l$ là độ dài đường sinh, $SH = h$ là chiều cao hình nón.

Trong tam giác vuông $SOA$ ta có:

$\eqalign{ & S{A^2} = S{O^2} + O{A^2} = {h^2} + {r^2} = {20^2} + {25^2} = 1025 \cr  & \Rightarrow SA = \sqrt {1025} \cr}$ 

Diện tích xung quanh hình nón là:

${S_{xq}} = \pi rl = \pi .25\sqrt {1025}  \approx 2514,5\left( {c{m^2}} \right)$

b) Thể tích khối nón là:

$V = {1 \over 3}\pi {r^2}h = {1 \over 3}\pi {.25^2}.20 \approx 13083,3\left( {c{m^3}} \right)$

c) Giả sử thiết diện $SAB$ đi qua đỉnh $S$ cắt đường tròn đáy tại $A$ và $B$. Gọi $I$ là trung điểm của dây cung $AB$. Từ tâm $O$ của đáy vẽ $OH$ vuông góc với $SI$.

Ta có $\left\{ \matrix{ AB \bot OI \hfill \cr  AB \bot SO \hfill \cr} \right. \Rightarrow AB \bot \left( {SOI} \right) \Rightarrow AB \bot OH$

Từ đó $\left\{ \matrix{ OH \bot AB \hfill \cr  OH \bot SI \hfill \cr} \right. \Rightarrow OH \bot \left( {SAB} \right) \Rightarrow OH = 12cm$

Trong tam giác vuông $SOI$ ta có: ${1 \over {O{H^2}}} = {1 \over {O{I^2}}} + {1 \over {O{S^2}}}$

$\eqalign{ & \Rightarrow {1 \over {O{I^2}}} = {1 \over {O{H^2}}} - {1 \over {O{S^2}}} \cr  & = {1 \over {{{12}^2}}} - {1 \over {{{20}^2}}} = {{256} \over {57600}} = {1 \over {225}} \cr  & \Rightarrow OI = 15cm \cr}$

Xét tam giác vuông $OAI$ ta có $AI^2 = OA^2 – OI^2 = 25^2 – 15^2 = 20^2$

Vậy $AI = 20cm$

Ta có: $SI.OH = SO.OI \Rightarrow SI = {{SO.OI} \over {OH}} = {{20.15} \over {12}} = 15cm$  

Vậy diện tích thiết diện $SAB$ là: ${S_{SAB}} = {1 \over 2}SI.AB = {1\over2}25.20 = 250\left( {c{m^2}} \right)$

Bài 4 trang 39 sách giáo khoa hình học lớp 12

Trong không gian cho hai điểm $A, B$ cố định và có độ dài $AB = 20 cm$. Gọi $d$ là một đường thẳng thay đổi luôn luôn đi qua $A$ và cách $B$ một khoảng  bằng $10 cm$. Chứng tỏ rằng đường thẳng $d$ luôn luôn nằm trên một mặt nón, hãy xác định trục và góc ở đỉnh của mặt nón đó.

Giải:

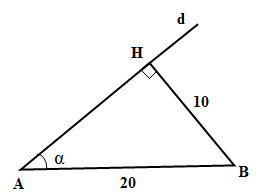
Kẻ $BH \bot d$ ta có $BH = 10cm$

Gọi $\alpha  = \widehat {ABH}$

Ta có $\sin \alpha  = {{BH} \over {AB}} = {1 \over 2} \Rightarrow \alpha  = {30^0}$ 

Vậy đường thẳng $d$ luôn thuộc mặt nón nhận đường thẳng $AB$ làm trục và có góc ở đỉnh bằng $2α = 60^0$

Giaibaitap.me