Bài 5 trang 39 sách giáo khoa hình học lớp 12

Một hình trụ có bán kính đáy $r = 5cm$ và có khoảng cách giữa hai đáy bằng $7 cm$.

a) Tính diện tích xung quanh của hình trụ và thể tích của khối trụ được tạo nên.

b) Cắt khối trụ bởi một mặt phẳng song song với trục và cách trục $3 cm$. Hãy tính diện tích của thiết diện được tạo nên.

Giải:

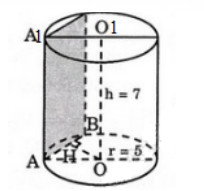
a) Theo đầu bài, hình trụ có chiều cao $h = 7 cm$ và bán kính đáy $r = 5 cm$.

Vậy diện tích xung quanh bằng:

$S_{xq}= 2πrh = 70π$($cm^2$)

Thể tích của khối trụ là:

             $V = πr^2h = 175π$ ($cm^3$)

b) Thiết diện là hình chữ nhật có một cạnh bằng chiều cao của hình trụ bằng $7 cm$. Giả sử thiết diện là $ABB_1A_1$.

Ta có $AA_1 = 7 cm, OH= 3 cm$.

Do tam giác $OAH$ vuông tại $H$ nên 

            $AH^2 = OA^2 – OH^2 = 25 – 9 = 16$.

Vậy $AH = 4 cm, AB = 8 cm$.

Diện tích của thiết diện là:

$S=AB.AA_1=8.7=56$ ($cm^2$).

Bài 6 trang 39 sách giáo khoa hình học lớp 12

Cắt một hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác đều canh $2a$. Tính diện tích xung quanh và thể tích của hình nón đó.

Giải:

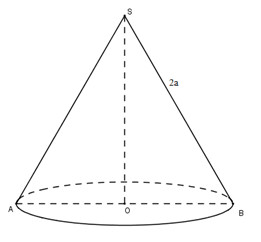
Theo đề bài, đường kính của hình tròn đáy của nón bằng $2a$. Vậy bán kính $R = a$.

Chiều cao của hình nón bằng chiều cao của tam giác đều, nên $h = a\sqrt3$ và đường sinh $l = 2a$.

Vậy diện tích xung quanh của hình nón là:

                            $S_{xq} = πRl = 2a^2π$

Thể tích khối nón là:

                            $V = {1 \over 3}\pi {r^2}.h = {1 \over 3}\pi {a^2}.a\sqrt 3  = {{\pi {a^3}\sqrt 3 } \over 3}$

Bài 7 trang 39 sách giáo khoa hình học lớp 12

Một hình trụ có bán kính $r$ và chiều cao $h = r\sqrt3$.

a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ.

b) Tính thể tích khối trụ tạo nên bởi hình trụ đã cho.

c) Cho hai điểm $A$ và $B$ lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng $AB$ và trục của hình trụ bằng $30^0$. Tính khoảng cách giữa đường thẳng $AB$ và trục của hình trụ

Giải:

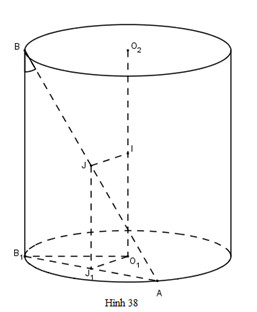
Theo công thức ta có:

$S_{xq} = 2πrh = 2\sqrt3 πr^2$ 

$S_{tp} = 2πrh + 2πr^2 =  2\sqrt3 πr^2 + 2 πr^2$

$= 2(\sqrt3 + 1)πr^2$  ( đơn vị thể tích)

b) $V$trụ = $πR^2h = \sqrt3 π r^3$

c) Giả sử trục của hình trụ là $O_1O_2$ và $A$ nằm trên đường tròn tâm $O_1$, $B$ nằm trên đường tròn tâm $O_2$; $I$ là trung điểm của $O_1O_2$ , $J$ là trung điểm của $AB$. Khi đó $IJ$ là đường vuông góc chung của $O_1O_2$  và $AB$. Hạ $BB_1$ vuông góc với đáy, $J_1$ là hình chiếu vuông góc của $J$ xuống đáy.

Ta có $J_{1}$ là trung điểm của $AB_{1}$, $O_{1}J_{1}$ = $IJ$.

Theo giả thiết $\widehat{B_{1}BA}$ = $30^0$^.

do vậy: $AB_1 = BB_1.tan 30^0$ = $\frac{\sqrt{3}}{3}h = r$.

Xét tam giác vuông $O_1J_1A$ vuông tại $J_1$ ta có: 

$O_{1}J^{2}_{1}$ = $O_{1}A^{2}$ - $AJ^{2}_{1} =$ $r^{2} - {\left( {{r \over 2}} \right)^2}=$ $\frac{3}{4}r^{2}$.

Vậy khoảng cách giữa $AB$ và $O_1O_2$ là: $\frac{\sqrt{3}}{2}r$

Giaibaitap.me