Bài 7 trang 44 sách sgk giải tích 12

Cho hàm số y = \(\frac{1}{4}x^{4}+\frac{1}{2}x^{2}+m\).

         a) Với giá trị nào của tham số \(m\), đồ thị của hàm số đi qua điểm \((-1 ; 1)\) ?

         b) Khảo sát sự biến thiên và vẽ đồ thị \((C)\) của hàm số khi \(m = 1\).

         c) Viết phương trình tiếp tuyến của \((C)\) tại điểm có tung độ bằng \(\frac{7}{4}\).

Giải

a) Điểm \((-1 ; 1)\) thuộc đồ thị của hàm số \(⇔1=\frac{1}{4}(-1)^{4}+\frac{1}{2}(-1)^{2}+m\Leftrightarrow m=\frac{1}{4}\).

b) \(m = 1\) \(\Rightarrow y=\frac{1}{4}x^{4}+\frac{1}{2}x^{2}+1\) .

Tập xác định:\(\mathbb R\).

* Sự biến thiên:

\(y'=x^{3}+x=x(x^{2}+1); y' = 0 ⇔ x = 0\).

- Hàm số đồng biến trên khoảng \((0;+\infty)\), nghịch biến trên khoảng \((-\infty;0)\)

- Cực trị:

    Hàm số đạt cực tiểu tại \(x=0\); \(y_{CT}=1\)

- Giới hạn: 

   \(\eqalign{
& \mathop {\lim y}\limits_{x \to - \infty } = + \infty \cr
& \mathop {\lim y}\limits_{x \to + \infty } = + \infty \cr} \)

- Bảng biến thiên:

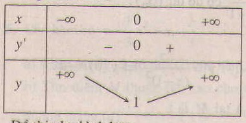
* Đồ thị 

Đồ thị hàm số giao trục \(0y\) tại điểm \((0;1)\).

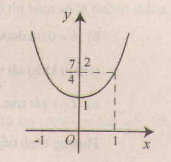
 c) \(\frac{1}{4}x^{4}+\frac{1}{2}x^{2}+1=\frac{7}{4}\Leftrightarrow x^{4}+2x^{2}-3=0\Leftrightarrow x^{2}=1\Leftrightarrow x=\pm 1.\)Vậy hai điểm thuộc \((C)\) có tung độ \(\frac{7}{4}\) là \(A(1 ; \frac{7}{4})\) và \(B(-1 ; \frac{7}{4})\). Ta có \(y'(-1) = -2, y'(1) = 2\).

Phương trình tiếp tuyến với \((C)\) tại \(A\) là: \(y - \frac{7}{4}= y'(1)(x - 1) ⇔ y = 2x -\frac{1}{4}\)

Phương trình tiếp tuyến với \((C)\) tại \(B\) là : \(y - \frac{7}{4}= y'(-1)(x + 1) ⇔ y = -2x - \frac{1}{4}\).

Bài 8 trang 44 sách sgk giải tích 12

Cho hàm số \(y = {x^3} + (m + 3){x^2} + 1 - m\) (m là tham số) có đồ thị là (C_m).

a) Xác định \(m\) để hàm số có điểm cực đại là \(x=-1\).

b) Xác định \(m\) để đồ thị (C_m) cắt trục hoành tại \(x=-2\).

Giải

 a) \(y' = 3{x^2} + 2(m + 3)x = x\left[ {3x + 2(m + 3)} \right]\);

\(y' = 0 \Leftrightarrow {x_1} = 0\) hoặc \({x_2} =  - {{2m + 6} \over 3}\)

Xảy ra hai trường hợp đối với dấu của \(y'\):

Trường hợp 1: \(x_1<x_2\)

Bảng biến thiên:

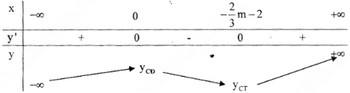
Trường hợp này hàm số đạt cực đại tại \(x=0\) do đó trường hợp này loại.

Trường hợp 2: \(x_2<x_1\)

Bảng biến thiên:

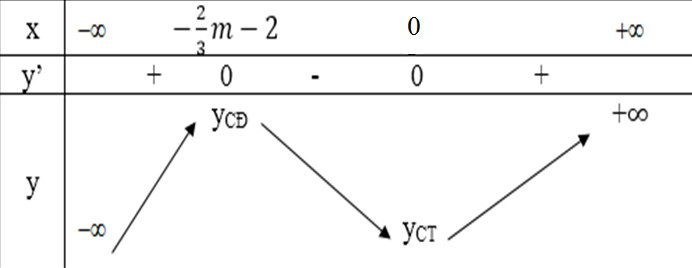
Để hàm số có điểm cực đại tại \(x = -1\) ta phải có

 \({x_2} =  - {{2m + 6} \over 3} =  - 1 \Leftrightarrow m =  - {3 \over 2}\)

(Chú ý : trường hợp \(x_1= x_2\) thì hàm số không có cực trị).

b) (C_m) cắt \(Ox\) tại \(x = -2\)\( ⇔ -8 + 4(m + 3) + 1 - m = 0 ⇔\) \(m =  - {5 \over 3}\).

Bài 9 trang 44 sách sgk giải tích 12

Cho hàm số \(y=\frac{(m+1)x-2m+1}{x-1}\) (m là tham số) có đồ thị là \((G)\).

a) Xác định \(m\) để đồ thị \((G)\) đi qua điểm \((0 ; -1)\).

b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số với \(m\) tìm được.

c) Viết phương trình tiếp tuyến của đồ thị trên tại giao điểm của nó với trục tung.

Giải

a) \((0 ; -1) ∈ (G) ⇔\)\(-1=\frac{(m+1)\cdot 0-2m+1}{0-1}\Leftrightarrow m=0.\)

b) \(m = 0\) ta được hàm số \(y=\frac{x+1}{x-1}\)  (G₀).

Tập xác định: \(D=\mathbb R \backslash {\rm{\{ }}1\}\)

* Sự biến thiên: 

\(y' = {{ - 2} \over {{{(x - 1)}^2}}} < 0\forall x \in D\)

- Hàm số nghịch biến trên khoảng: \((-\infty;1)\) và \((1;+\infty)\).

- Cực trị:

    Hàm số không có cực trị.

- Tiệm cận:

    \(\eqalign{
& \mathop {\lim y}\limits_{x \to \pm \infty } = 1 \cr
& \mathop {\lim y}\limits_{x \to {1^ - }} = - \infty \cr
& \mathop {\lim y}\limits_{x \to {1^ + }} = + \infty \cr} \)

Tiệm cận đứng là: \(x=1\), tiệm cận ngang là: \(y=1\)

- Bảng biến thiên:

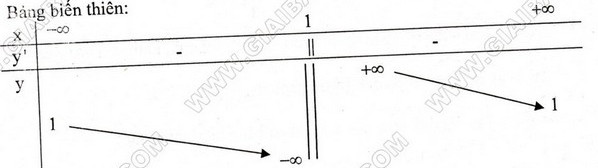
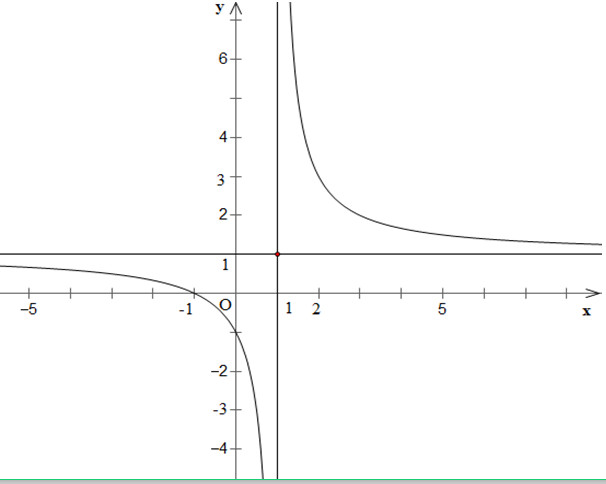
* Đồ thị:

Đồ thị hàm số giao trục \(Ox\) tại \((-1;0)\), trục \(Oy\) tại \((0;-1)\)

Đồ thị hàm số nhận \(I(1;1)\) làm tâm đối xứng.

c) (G₀) cắt trục tung tại \(M(0 ; -1)\). 

\(y'=\frac{-2}{(x-1)^{2}}\Rightarrow y'(0) = -2\).

Phương trình tiếp tuyến của (G₀) tại \(M\) là : \(y - (-1) = y'(0)(x - 0) ⇔ y= -2x - 1\).

Giaibaitap.me