Bài 4 trang 44 sách sgk giải tích 12

Bằng cách khảo sát hàm số, hãy tìm số nghiệm của các phương trình sau:

a) \({x^3}-3{x^2} + 5 = 0\);      

b) \(- 2{x^3} + 3{x^2}-2 = 0\) ;      

c) \(2{x^2}-{x^4} =  - 1\).

Giải:

a) Xét hàm số \(y ={x^3}-3{x^2} + 5\) .

Tập xác định : \(\mathbb R\).

* Sự biến thiên:

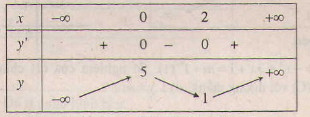
\(y'{\rm{ }} = 3{x^{2}} - {\rm{ }}6x{\rm{ }} = {\rm{ }}3x\left( {x{\rm{ }} - {\rm{ }}2} \right)\); \(y' = 0 ⇔ x = 0,x = 2\).

- Hàm số đồng biến trên khoảng \((-\infty;0)\) và \((2;+\infty)\); nghịch biến trên khoảng \((0;2)\).

- Cực trị: 

     Hàm số đạt cực đạt tại \(x=0\); \(y_{CĐ}=5\)

     Hàm số đạt cực tiểu tại \(x=2\); \(y_{CT}=1\)

- Giới hạn:   

\(\eqalign{
& \mathop {\lim y}\limits_{x \to - \infty } = - \infty \cr 
& \mathop {\lim y}\limits_{x \to + \infty } = + \infty \cr} \)

Bảng biến thiên:

* Đồ thị 

Đồ thị giao \(Oy\) tại điểm \((0;5)\)

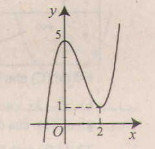
Số nghiệm của phương trình chính là giao của đồ thị hàm số \(y ={x^3}-3{x^2} + 5\) và trục hoành. Do đó từ đồ thị ta thấy phương trình có nghiệm duy nhất.

b) Xét hàm số \(y =- 2{x^3} + 3{x^2}\).

Tập xác định : \(\mathbb R\).

Sự biến thiên:

    \(y'= - 6{x^{2  + }}6x = -6x(x - 1); y' = 0 ⇔ x = 0,x = 1\).

- Hàm số đồng biến trên khoảng: \((-\infty;0)\) và \((1;+\infty)\); nghịch biến trên khoảng \((0;1)\).

- Cực trị:

    Hàm số đạt cực đại tại \(x=0\); \(y_{CĐ}=0\).

    Hàm số đạt cực tiểu tại \(x=1\); \(y_{CT}=-1\)

- Giới hạn: 

\(\eqalign{
& \mathop {\lim y}\limits_{x \to - \infty } = - \infty \cr 
& \mathop {\lim y}\limits_{x \to + \infty } = + \infty \cr} \)

Bảng biến thiên:

* Đồ thị 

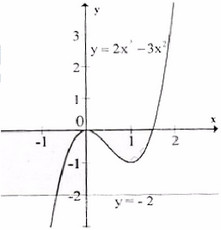
Số nghiệm của phương trình là giao điểm của đồ thị hàm số \(y =- 2{x^3} + 3{x^2}\) với đường thẳng \(y=2\). Từ đồ thị ta thấy phương trình có nghiệm duy nhất.

c) Xét hàm số \(y = f(x) =2{x^2}-{x^4}\)

Tập xác định : \(\mathbb R\).

Sự biến thiên:

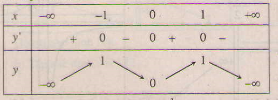
\(y' = 4x -4{x^{3}} = 4x(1- {x^2})\); \(y' = 0 ⇔ x = 0,x = ±1\).  

- Hàm số đồng biến trên khoảng: \((-\infty;-1)\) và \((0;1)\), nghịch biến trên khoảng \((-1;0)\) và \((1;+\infty)\).

- Cực trị:

    Hàm số đạt cực đại tại hai điểm \(x=-1\) và \(x=1\); \(y_{CĐ}=1\).

    Hàm số đạt cực tiểu tại \(x=0\); \(y_{CT}=0\)

- Giới hạn:

\(\eqalign{
& \mathop {\lim y}\limits_{x \to - \infty } = - \infty \cr 
& \mathop {\lim y}\limits_{x \to + \infty } = - \infty \cr} \)

Bảng biến thiên:

* Đồ thị

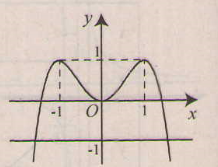
Số nghiệm của phương trình là giao của đồ thị hàm số \(y = f(x) =2{x^2}-{x^4}\) và đường thẳng \(y = -1\), từ đồ thị ta thấy phương trình đã cho có hai nghiệm phân biệt.

Bài 5 trang 44 sách sgk giải tích 12

a) Khảo sát sự biến thiên và vẽ đồ thị \((C)\) của hàm số

                                   \(y = -x^3+ 3x + 1\).

b) Dựa vào đồ thị \((C)\), biện luận về số nghiệm của phương trình sau theo tham số \(m\).

                                   \(x^3- 3x + m = 0\).

Giải:

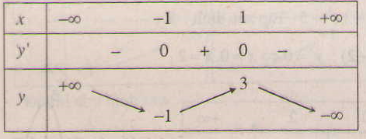
 a) Xét hàm số  \(y = -x^3+ 3x + 1\).

Tập xác định : \(\mathbb R\).

* Sự biến thiên:

\(y' = -3x^2+ 3 = -3(x^2-1)\); \(y' = 0 ⇔ x = -1,x = 1\).

- Hàm số đồng biến trên khoảng \((-1;1)\), nghịch biến trên khoảng \((-\infty;-1)\) và \((1;+\infty)\).

- Cực trị:

    Hàm số đạt cực đại tại \(x=1\); \(y_{CĐ}=3\)

    Hàm số đạt cực tiểu tại \(x=-1\); \(y_{CT}=-1\)

- Giới hạn:

\(\eqalign{
& \mathop {\lim y}\limits_{x \to - \infty } = + \infty \cr 
& \mathop {\lim y}\limits_{x \to + \infty } = - \infty \cr} \)

Bảng biến thiên:

* Đồ thị:

Đồ thị giao \(Oy\) tại điểm \(I(0;1)\) và nhận \(I\) làm tâm đối xứng.

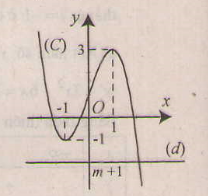
b) \(x^3- 3x + m = 0\) \(⇔ -x^3+ 3x + 1 = m + 1\) (1). Số nghiệm của (1) chính là  số giao điểm của đồ thị hàm số (C) với đường thẳng (d) : \(y = m + 1\).

Từ đồ thị ta thấy :

       +)  \(m + 1 < -1 ⇔ m < -2 \): (d) cắt (C) tại 1 điểm, (1) có 1 nghiệm.

       +)  \(m + 1 = -1 ⇔ m = -2\) : (d) cắt (C) tại 1 điểm và tiếp xúc với (C) tại 1 điểm, (1) có 2 nghiệm.

       +)  \(-1 < m + 1 < 3 ⇔ -2 < m < 2\) : (d) cắt (C) tại 3 điểm, (1) có 3 nghiệm.

       +)  \( m + 1 = 3 ⇔ m = 2\) : (d) cắt (C) tại 1 điểm và tiếp xúc với (C) tại 1 điểm, (1) có 2 nghiệm.

       +)   \(m + 1 > 3 ⇔ m > 2\) : (d) cắt (C) tại 1 điểm, (1) có 1 nghiệm.

Bài 6 trang 44 sách sgk giải tích 12

Cho hàm số  \(y = {{mx - 1} \over {2x + m}}\) .

         a) Chứng minh rằng với mọi giá trị của tham số \(m\), hàm số luôn đồng biến trên mỗi khoảng xác định của nó.

         b) Xác định m để tiệm cận đứng đồ thị đi qua \(A(-1 ; \sqrt2)\).

         c) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi \(m = 2\).

Giải:

a) \(y = {{mx - 1} \over {2x + m}}\).

Tập xác định: \(\mathbb R\backslash \left\{ {{{ - m} \over 2}} \right\}\)  ;

 \(y' = {{{m^2} + 2} \over {{{(2x + m)}^2}}} > 0,\forall x \ne  - {m \over 2}\)

  Do đó hàm số luôn đồng biến trên mỗi khoảng xác định của nó.

b) Tiệm cận đứng \(∆\) : \(x =  - {m \over 2}\).

          \(A(-1 ; \sqrt2) ∈ ∆\) \(⇔- {m \over 2}= -1 ⇔ m = 2\).

c) \(m = 2\) thì hàm số đã cho có phương trình là:

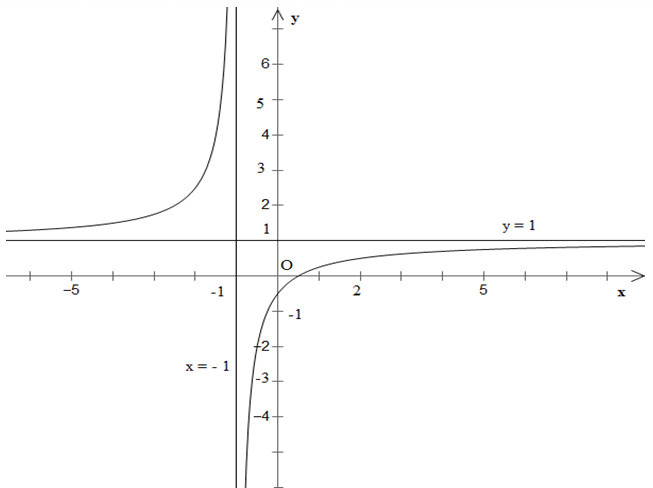
\(y = {{2x - 1} \over {2x + 2}}\).

Tập xác đinh: \(D=\mathbb R\backslash {\rm{\{ }} - 1\} \)

* Sự biến thiên:

\(y' = {6 \over {{{(2x + 2)}^2}}} > 0\forall x \in D\)

- Hàm số đồng biến trên khoảng: \((-\infty;-1)\) và \((-1;+\infty)\)

- Cực trị:

    Hàm số không có cực trị.

- Tiệm cận:

   \(\eqalign{
& \mathop {\lim y}\limits_{x \to \pm \infty } = 1 \cr 
& \mathop {\lim y}\limits_{x \to - {1^ - }} = + \infty \cr 
& \mathop {\lim y}\limits_{x \to - {1^ + }} = - \infty \cr} \)

Tiệm cận đứng là \(x=-1\), tiệm cận ngang là: \(y=1\)

- Bảng biến thiên

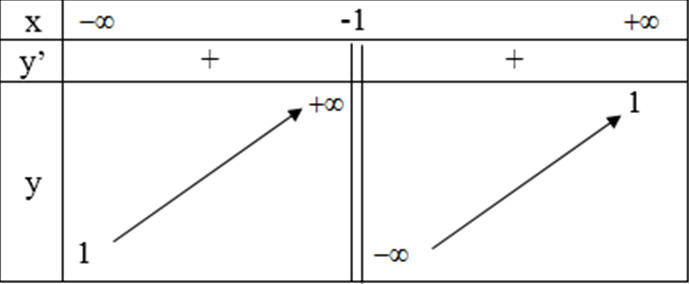
* Đồ thị

Đồ thị hàm số giao \(Ox\) tại điểm \(({1\over 2};0)\), giao \(Oy\) tại điểm \((0;{-1\over 2})\).

Đồ thị hàm số nhận điểm \(I(-1;1)\) làm tâm đối xứng.

Giaibaitap.me