Bài 4 trang 10 sách sgk giải tích 12
Chứng minh rằng hàm số \(y=\sqrt {2x - {x^2}}\) đồng biến trên khoảng \((0 ; 1)\) và nghịch biến trên các khoảng \((1 ; 2)\).
Giải:
Tập xác định : \(D = [0 ; 2]\); \(y' = \frac{1-x}{^{\sqrt{2x-x^{2}}}}\), \(\forall x \in (0;2)\); \(y' = 0 \)\(\Leftrightarrow x=1\)
Bảng biến thiên :
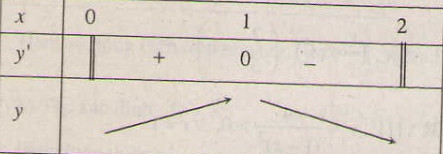
Vậy hàm số đồng biến trên khoảng \((0 ; 1)\) và nghịch biến trên khoảng \((1 ; 2)\).
Bài 5 trang 10 sách sgk giải tích 12
Chứng minh các bất đẳng thức sau:
a) \(tanx > x\) \((0 < x < \frac{\pi }{2})\);
b) \(tanx > x + \frac{x^{3}}{3} (0 < x < \frac{\pi }{2})\).
Giải:
a) Xét hàm số \(y = f(x) = tanx – x\) với \(x ∈ (0 ; \frac{\pi }{2})\).
Ta có : \(y’\) = \(\frac{1}{cos^{2}x} - 1 ≥ 0\), \(x ∈ (0 ; \frac{\pi }{2})\); \(y’ = 0 ⇔ x = 0\). Vậy hàm số luôn đồng biến trên \((0 ; \frac{\pi }{2})\).
Từ đó \(∀x ∈ (0 ; \frac{\pi }{2})\) thì \(f(x) > f(0)\)
\(⇔ tanx – x > tan0 – 0 = 0\) hay \(tanx > x\).
b) Xét hàm số \(y = g(x) = tanx – x\) - \(\frac{x^{3}}{3}\). với \(x ∈ (0 ; \frac{\pi }{2})\).
Ta có : \(y’ = \frac{1}{cos^{2}x} - 1 -x^2\)=\(1 + {\tan ^2}x - 1 - {x^2} = (ta{n^2}x - {x^2})\)
= \((tanx - x)(tanx + x)\), \(∀x ∈ (0 ;\frac{\pi }{2} )\).
Vì \(∀x ∈ (0 ; \frac{\pi }{2})\) nên \(tanx +x ≥ 0\) và \(tanx - x >0\) (theo câu a).
Do đó \(y' ≥ 0, ∀x ∈ (0 ;\frac{\pi }{2})\).
Dễ thấy \(y' = 0 ⇔ x = 0\). Vậy hàm số luôn đồng biến trên (0 ; \(\frac{\pi }{2}\)). Từ đó : \(∀x ∈ (0 ; \frac{\pi }{2})\) thì \(g(x) > g(0) \)\(⇔ tanx – x - \frac{x^{3}}{3}\) \(> tan0 - 0 - 0 = 0\) hay \( tanx > x + \frac{x^{3}}{3}\).
Giaibaitap.me
Giải bài tập trang 18 bài 2 cực trị của hàm số SGK Giải tích 12. Câu 1: Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm số sau:...
Giải bài tập trang 18 bài 2 cực trị của hàm số SGK Giải tích 12. Câu 4: Chứng minh rằng với mọi giá trị của tham số, hàm số sau luôn luôn có một điểm cực đại và một điểm cực tiểu....
Giải bải tập trang 23, 24 bài 3 giá trị lớn nhất và giá trị nhỏ nhất của hàm số SGK Giải tích 12. Câu 1: Tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:...
Giải bài tập trang 24 bài 3 giá trị lớn nhất và giá trị nhỏ nhất của hàm số SGK Giải tích 12. Câu 4: Tính giá trị lớn nhất của các hàm số sau...
