Bài 2.33 trang 125 Sách bài tập (SBT) Giải tích 12

Giải các phương trình logarit sau:

a) \(\log x + \log {x^2} = \log 9x\)

b) \(\log {x^4} + \log 4x = 2 + \log {x^3}$\)

c) \({\log _4}{\rm{[}}(x + 2)(x + 3){\rm{]}} + {\log _4}\frac{{x - 2}}{{x + 3}} = 2\)

d) \({\log _{\sqrt 3 }}(x - 2){\log _5}x = 2{\log _3}(x - 2)\)

Hướng dẫn làm bài:

a) Với điều kiện x > 0, ta có

\(\log x + 2\log x = \log 9 + \log x\)

\(\Leftrightarrow \log x = \log 3  \Leftrightarrow  x = 3\)

b) Với điều kiện  x > 0, ta có

\(4\log x + \log 4 + \log x = 2\log 10 + 3\log x\)

\( \Leftrightarrow \log x = \log 5 \Leftrightarrow x = 5\)

c) Ta có điều kiện của phương trình đã cho là:

\(\left\{ {\matrix{{(x + 2)(x + 3) > 0} \cr {{{x - 2} \over {x + 3}} > 0} \cr} } \right. \Leftrightarrow \left\{ {\matrix{{\left[ {\matrix{{x < - 3} \cr {x > - 2} \cr} } \right.} \cr {\left[ {\matrix{{x < - 3} \cr {x > 2} \cr} } \right.} \cr} } \right. \Leftrightarrow \left[ {\matrix{{x < - 3} \cr {x > 2} \cr} (1)} \right.\)

Khi đó, phương trình đã cho tương đương với:

\({\log _4}{\rm{[}}(x + 2)(x + 3)\frac{{x - 2}}{{x + 3}}{\rm{]}}\)

\(= {\log _4}16  \Leftrightarrow {x^2} - 4 = 16 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x = 2\sqrt 5 }\\
{x = - 2\sqrt 5 }
\end{array}} \right.\)             

Cả hai nghiệm trên đều thỏa mãn điều kiện (1).

d) Với điều kiện  x > 2, ta có phương trình

\(2{\log _3}(x - 2)({\log _5}x - 1) = 0\)

\(  \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{{{\log }_3}(x - 2) = 0}\\
{{{\log }_5}x - 1 = 0}
\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x = 3}\\
{x = 5}
\end{array}} \right.} \right.\)                    

Cả hai giá trị này đều thỏa mãn điều kiện x > 2.

Bài 2.34 trang 125 Sách bài tập (SBT) Giải tích 12

Giải các phương trình sau bằng phương pháp đồ thị:

a) \({\log _{\frac{1}{3}}}x = 3x\)                                                                      

b) \({\log _3}x =  - x + 11\)

c) \({\log _4}x = \frac{4}{x}\)                                                                       

d) \({16^x} = {\log _{\frac{1}{2}}}x\)

Hướng dẫn làm bài:

a) Vẽ đồ thị của hàm số \({\log _{\frac{1}{3}}}x = 3x\)    và đường thẳng y = 3x trên cùng một hệ trục tọa độ (H.61), ta thấy chúng cắt nhau tại điểm có hoành độ \(x = \frac{1}{3}\)

Thử lại, ta thấy giá trị này thỏa mãn phương trình đã cho. Mặt khác, hàm số \(y = {\log _{\frac{1}{3}}}x\) luôn nghịch biến, hàm số  y = 3x luôn đồng biến. Vậy \(x = \frac{1}{3}\) là nghiệm duy nhất của phương trình đã cho.

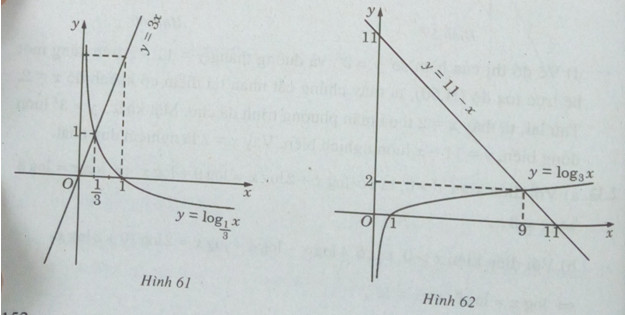
b) Vẽ đồ thị của hàm số \(y = {\log _3}x\) và đường thẳng y = - x + 11 trên cùng một hệ trục tọa độ (H.62) , ta thấy chúng cắt nhau tại điểm có hoành độ x = 9. Lập luận tương tự câu a), ta cũng có đây là nghiệm duy nhất của phương trình đã cho.

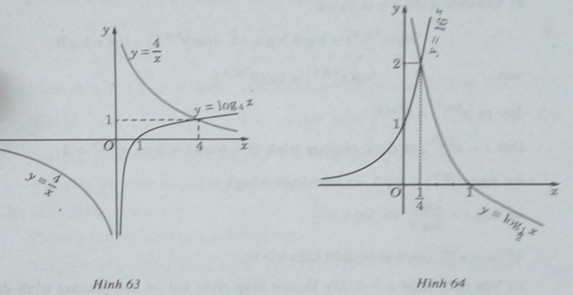
c) Vẽ đồ thị của các hàm số \(y = {\log _4}x\) và \(y = \frac{4}{x}\) trên cùng một hệ trục tọa độ (H.63), ta thấy chúng cắt nhau tại điểm có hoành độ x = 4. Ta cũng có hàm số \(y = {\log _3}x\) luôn đồng biến, hàm số \(y = \frac{4}{x}\) luôn nghịch biến trên \((0; + \infty )\) . Do đó, x = 4 là nghiệm duy nhất.

 6

d) Vẽ đồ thị của các hàm số \(y = {16^x}\) và \(y = {\log _{\frac{1}{2}}}x\) trên cùng một hệ trục tọa độ (H.64), ta thấy chúng cắt nhau tại điểm có hoành độ \(x = \frac{1}{4}\) . Thử lại, ta thấy \(x = \frac{1}{4}\) thỏa mãn phương trình đã cho. Mặt khác, hàm số  luôn đồng biến, hàm số  luôn nghịch biến.

Vậy \(x = \frac{1}{4}\) là nghiệm duy nhất của phương trình.

Bài 2.35 trang 125 Sách bài tập (SBT) Giải tích 12

Giải các phương trình logarit :

a) \({\log _2}({2^x} + 1).{\log _2}({2^{x + 1}} + 2) = 2\)

b) \({x^{\log 9}} + {9^{\log x}} = 6\)

c) \({x^{3{{\log }^3}x - \frac{2}{3}\log x}} = 100\sqrt[3]{{10}}\)                                                          

d) \(1 + 2{\log _{x + 2}}5 = {\log _5}(x + 2)\)

Hướng dẫn làm bài:

a) \({\log _2}({2^x} + 1).{\log _2}{\rm{[}}2({2^x} + 1){\rm{]}} = 2\)

\( \Leftrightarrow {\log _2}({2^x} + 1).{\rm{[}}1 + {\log _2}({2^x} + 1){\rm{]}} = 2\)

Đặt \(t = {\log _2}({2^x} + 1)\) , ta có phương trình  

\(t(1 + t) = 2 ⇔ {t^2} + t – 2 = 0\)

\(\eqalign{& \Leftrightarrow \left[ {\matrix{{t = 1} \cr {t = - 2} \cr} } \right. \Leftrightarrow \left[ {\matrix{{{{\log }_2}({2^x} + 1) = 1} \cr {{{\log }_2}({2^x} + 1) = - 2} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{{2^x} + 1 = 2} \cr {{2^x} + 1 = {1 \over 4}} \cr} } \right. \Leftrightarrow \left[ {\matrix{{{2^x} = 1} \cr {{2^x} = - {3 \over 4}(l)} \cr} } \right. \Leftrightarrow x = 0 \cr} \)

b) Với điều kiện x > 0, ta có: \(\log ({x^{\log 9}}) = \log ({9^{\log x}})\)

\(\log ({x^{\log 9}}) = \log 9.\log x\)  và \(\log ({9^{\log x}}) = \log x.\log 9\)

Nên \(\log ({x^{\log 9}}) = \log ({9^{\log x}})\)   

Suy ra:

\({t^4} + 14{t^2} - 32t + 17 = 0\)

\( \Leftrightarrow {(t - 1)^2}({t^2} + 2t + 17) = 0 \Leftrightarrow t = 1\)  \({x^{\log 9}} = {9^{\log x}}\)

Đặt \(t = {x^{\log 9}}\)  , ta được phương trình \(2t = 6 ⇔ t = 3 ⇔ {x^{\log 9}} = 3\) 

\(\eqalign{
& \Leftrightarrow \log ({x^{\log 9}}) = \log 3 \cr 
& \Leftrightarrow \log 9.\log x = \log 3 \cr 
& \Leftrightarrow \log x = {{\log 3} \over {\log 9}} \cr 
& \Leftrightarrow \log x = {1 \over 2} \cr}\)

\(\Leftrightarrow x = \sqrt {10} \) (thỏa mãn điều kiện x > 0)

c) Với điều kiện x > 0, lấy logarit thập phân hai vế của phương trình đã cho, ta được:

    \((3{\log ^3}x - \frac{2}{3}\log x).\log x = \frac{7}{3}\)               

Đặt \(t = \log x\) , ta được phương trình \(3{t^4} - \frac{2}{3}{t^2} - \frac{7}{3} = 0\)

\(\eqalign{
& \Leftrightarrow 9{t^4} - 2{t^2} - 7 = 0 \Leftrightarrow \left[ \matrix{
{t^2} = 1 \hfill \cr 
{t^2} = - {7 \over 9}\left( {loại} \right) \hfill \cr} \right.\left[ \matrix{
t = 1 \hfill \cr 
t = - 1 \hfill \cr} \right. \cr 
& \Leftrightarrow \left[ \matrix{
\log x = 1 \hfill \cr 
\log x = - 1 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
x = 10 \hfill \cr 
x = {1 \over {10}} \hfill \cr} \right. \cr} \)

d) Đặt \(t = {\log _5}(x + 2)\) với điều kiện \(x + 2{\rm{ }} > 0,\,\,x + 2 \ne 1\) , ta có:

\(\eqalign{& 1 + {2 \over t} = t \Leftrightarrow {t^2} - t - 2 = 0,t \ne 0 \cr & \Leftrightarrow \left[ {\matrix{{t = - 1} \cr {t = 2} \cr} } \right. \Leftrightarrow \left[ {\matrix{{{{\log }_5}(x + 2) = - 1} \cr {{{\log }_5}(x + 2) = 2} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{x + 2 = {1 \over 5}} \cr {x + 2 = 25} \cr} \Leftrightarrow \left[ {\matrix{{x = - {9 \over 5}} \cr {x = 23} \cr} } \right.} \right. \cr} \)

Giaibaitap.me