Bài 3.43 trang 131 sách bài tập (SBT) – Hình học 12

Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Bằng phương pháp tọa độ hãy tính khoảng cách giữa hai đường thẳng CA’ và  DD’.

Hướng dẫn làm bài:

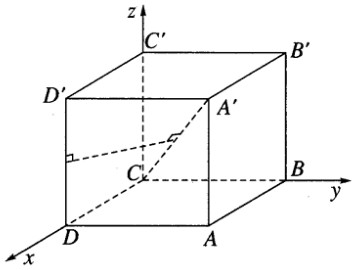
Ta chọn hệ trục tọa độ sao cho: C là gốc tọa độ,\(\overrightarrow {CD}  = a\overrightarrow i ;\overrightarrow {CB}  = a\overrightarrow j ;\overrightarrow {CC'}  = a\overrightarrow k \)

Trong hệ tọa độ vừa chọn ta có: C(0; 0; 0), A’(a; a ; a), D(a,; 0;0), D’(a; 0; a)

\(\overrightarrow {CA'}  = (a;a;a),\overrightarrow {{\rm{DD}}'}  = (0;0;a)\)

Gọi \((\alpha )\) là mặt phẳng chứa \(\overrightarrow {CA'} \) và song song với \(\overrightarrow {DD'} \) . Mặt phẳng \((\alpha )\) có vecto pháp tuyến là: \(\overrightarrow n  = \overrightarrow {CA'}  \wedge \overrightarrow {{\rm{DD}}'}  = ({a^2}; - {a^2};0)\)    hay x – y = 0

Phương trình tổng quát của \((\alpha )\) là x – y = 0.

Ta có: \(d(CA',{\rm{DD}}') = d(D,(\alpha )) = {{| - a|} \over {\sqrt {1 + 1 + 0} }} = {a \over {\sqrt 2 }}\)

Vậy khoảng cách giữa hai đường thẳng  CA’ và DD’ là  \({{a\sqrt 2 } \over 2}\)

Bài 3.44 trang 131 sách bài tập (SBT) – Hình học 12

Cho mặt phẳng \((\alpha )\) : 2x + y  +z – 1 = 0  và đường thẳng d: \({{x - 1} \over 2} = {y \over 1} = {{z + 2} \over { - 3}}\)

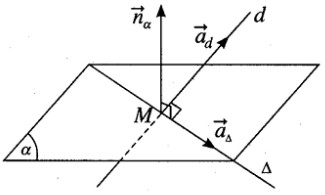
Gọi M là giao điểm của d và \((\alpha )\) , hãy viết phương trình của đường thẳng \(\Delta \) đi qua M vuông góc với d và nằm trong \((\alpha )\)

Hướng dẫn làm bài

Phương trình tham số của đường thẳng d: \(\left\{ {\matrix{{x = 1 + 2t} \cr {y = t} \cr {z = - 2 - 3t} \cr} } \right.\)

Xét phương trình:

\(2(1 + 2t) + (t) + ( - 2 – 3t) – 1 = 0  \Leftrightarrow 2t – 1 = 0 \Leftrightarrow  t = {1 \over 2}\)

Vậy đưởng thẳng d cắt mặt phẳng \((\alpha )\) tại điểm \(M(2;{1 \over 2}; - {7 \over 2})\).

Ta có vecto pháp tuyến của mặt phẳng \((\alpha )\) và vecto chỉ phương của đường thẳng d lần lượt là \(\overrightarrow {{n_\alpha }}  = (2;1;1)\)   và \(\overrightarrow {{a_d}}  = (2;1; - 3)\).

Gọi \(\overrightarrow {{a_\Delta }} \)   là vecto pháp tuyến của \(\Delta \), ta có \(\overrightarrow {{a_\Delta }}  \bot \overrightarrow {{n_\alpha }} \)  và \(\overrightarrow {{a_\Delta }}  \bot \overrightarrow {{a_d}} \).

Suy ra \(\overrightarrow {{a_\Delta }}  = \overrightarrow {{n_\alpha }}  \wedge \overrightarrow {{n_d}}  = ( - 4;8;0)\)  hay \(\overrightarrow {{a_\Delta }}  = (1; - 2;0)\)

Vậy phương trình tham số của \(\Delta \) là  \(\left\{ {\matrix{{x = 2 + t} \cr {y = {1 \over 2} - 2t} \cr {z = - {7 \over 2}} \cr} } \right.\)

Bài 3.45 trang 131 sách bài tập (SBT) – Hình học 12

Cho hai đường thẳng  d₁:  \({{x - 1} \over 2} = {{y + 2} \over { - 3}} = {{z - 5} \over 4}\)  và d₂: \(\left\{ {\matrix{{x = 7 + 3t} \cr {y = 2 + 2t} \cr {z = 1 - 2t} \cr} } \right.\)

a) Chứng minh rằng d₁ và d₂ cùng nằm trong một mặt phẳng \((\alpha )\).

b) Viết phương trình của \((\alpha )\).

Hướng dẫn làm bài:

a) Ta có  \(\overrightarrow {{a_{{d_1}}}}  = (2; - 3;4)\)  và \(\overrightarrow {{a_{{d_2}}}}  = (3;2; - 2)\)

\(\overrightarrow n  = \overrightarrow {{a_{{d_1}}}}  \wedge \overrightarrow {{a_{{d_2}}}}  = ( - 2;16;13)\)

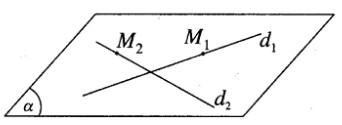
Lấy điểm M₁(1; -2; 5) trên d₁ và điểm M₂(7;2;1) trên d₂.

Ta có \(\overrightarrow {{M_1}{M_2}}  = (6;4; - 4)\)

     \(\overrightarrow n .\overrightarrow {{M_1}{M_2}}  =  - 12 + 64 - 52 = 0\)

Suy ra d1 và d2 cùng nằm trong mặt phẳng \((\alpha )\)

b) Mặt phẳng \((\alpha )\) chứa M1 và có vecto pháp tuyến là  \(\overrightarrow n \), vậy phương trình của \((\alpha )\) là:

\(– 2(x – 1)  +16(y + 2) + 13(z – 5) = 0\) hay \(2x – 16y – 13z + 31 = 0\)

Giaibaitap.me