Bài 1.26 trang 20 Sách bài tập (SBT) Giải tích 12
Tìm hai số có hiệu là 13 sao cho tích của chúng là bé nhất.
Hướng dẫn làm bài:
Gọi một trong hai số phải tìm là x, ta có số kia là x + 13
Xét tích:
\(\eqalign{
& p(x) = x(x + 13) = {x^2} + 13x \cr
& p'(x) = 2x + 13;p'(x) = 0 < = > x = - {{13} \over 2} \cr} \)
Bảng biến thiên:
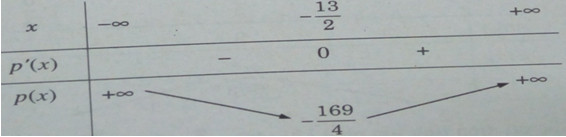
Vậy tích hai số bé nhất khi một số là \( - {{13} \over 2}\) và số kia là \({{13} \over 2}\).
Bài 1.27 trang 20 Sách bài tập (SBT) Giải tích 12
Một chất điểm chuyển động theo quy luật s = 6t2 – t3 . Tính thời điểm t (giây) tại đó vận tốc v (m/s) của chuyển động đạt giá trị lớn nhất.
Hướng dẫn làm bài:
\(s = 6{t^2} - {t^3},t > 0\)
Vận tốc chuyển động là v = s’ , tức là v = 12t – 3t2
Ta có: v’ = 12 – 6t
v’ = 0 ⇔ t = 2
Hàm số v đồng biến trên khoảng (0;2) và nghịch biến trên khoảng \((2; + \infty )\) .
Vận tốc đạt giá trị lớn nhất khi t = 2. Khi đó \(\mathop {\max }\limits_{(0; + \infty )} V = {V_{CD}} = v(2) = 12(m/s)\).
Bài 1.28 trang 20 Sách bài tập (SBT) Giải tích 12
Hãy tìm tam giác vuông có diện tích lớn nhất nếu tổng của một cạnh góc vuông và cạnh huyền bằng hằng số a (a > 0).
Hướng dẫn làm bài:
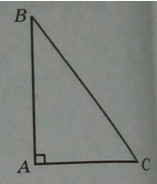
Kí hiệu cạnh góc vuông AB là x, \(0 < x < {a \over 2}\)
Khi đó, cạnh huyền BC = a – x , cạnh góc vuông kia là:
\(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{(a - x)}^2} - {x^2}} \)
Hay \(AC = \sqrt {{a^2} - 2ax} \)
Diện tích tam giác ABC là:
\(\eqalign{
& S(x) = {1 \over 2}x\sqrt {{a^2} - 2ax} \cr
& S'(x) = {1 \over 2}\sqrt {{a^2} - 2ax} - {1 \over 2}{{ax} \over {\sqrt {{a^2} - 2ax} }} = {{a(a - 3x)} \over {2\sqrt {{a^2} - 2ax} }} \cr
& S'(x) = 0 < = > x = {a \over 3} \cr} \)
Bảng biến thiên:

Tam giác có diện tích lớn nhất khi \(AB = {a \over 3};BC = {{2a} \over 3}\)
Giaibaitap.me
Giải bài tập trang 22, 23 bài 4 đường tiệm cận Sách bài tập (SBT) Giải tích 12. Câu 1: Tìm các tiệm cận đường và ngang của đồ thị mỗi hàm số sau...
Giải bài tập trang 33, 34 Sách bài tập (SBT) Giải tích 12 bài 5 khảo sát sự biến thiên và vẽ đồ thị của hàm số. Câu 1.34: Tìm m để hàm số...
Giải bài tập trang 34 Sách bài tập (SBT) Giải tích 12 bài 5 khảo sát sự biến thiên và vẽ đồ thị của hàm số. Câu 1.38: Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho...
Giải bài tập trang 35 Sách bài tập (SBT) Giải tích 12 bài 5 khảo sát sự biến thiên và vẽ đồ thị của hàm số. Câu 1.42: Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1)...
