Bài 1.14 trang 15 Sách bài tập (SBT) Giải tích 12

Tìm cực trị của các hàm số sau:

a) \(y = \sin 2x\)                                                             

b) \(y = \cos x - \sin x\)

c) \(y = {\sin ^2}x\)

Hướng dẫn làm bài:

a) \(y = \sin 2x\)               

Hàm số có chu kỳ \(T = \pi \)

Xét hàm số \(y = \sin 2x\) trên đoạn \({\rm{[}}0;\pi {\rm{]}}\) , ta có:

\(y' = 2\cos 2x\)

\(y = 0 \Leftrightarrow \left[ \matrix{
x = {\pi \over 4} \hfill \cr 
x = {{3\pi } \over 4} \hfill \cr} \right.\)

Bảng biến thiên:

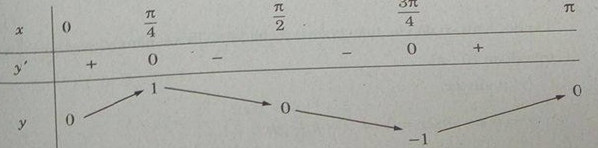
Do đó trên đoạn \({\rm{[}}0;\pi {\rm{]}}\) , hàm số đạt cực đại  tại \({\pi  \over 4}\) , đạt cực tiểu tại \({{3\pi } \over 4}\) và \({y_{CD}} = y({\pi  \over 4}) = 1;\,\,{y_{CT}} = y({{3\pi } \over 4}) =  - 1\)       

Vậy trên R ta có:

\({y_{CĐ}} = y({\pi  \over 4} + k\pi ) = 1;\)

\({y_{CT}} = y({{3\pi } \over 4} + k\pi ) =  - 1,k \in Z\)          

b)

Hàm số tuần hoàn chu kỳ  nên ta xét trên đoạn \({\rm{[}} - \pi ;\pi {\rm{]}}\).

\(\eqalign{
& y' = - \sin x - \cos x \cr 
& y' = 0 < => \tan x = - 1 < = > x = - {\pi \over 4} + k\pi ,k \in Z \cr} \)

 Lập bảng biến thiên trên đoạn \({\rm{[}} - \pi ;\pi {\rm{]}}\)

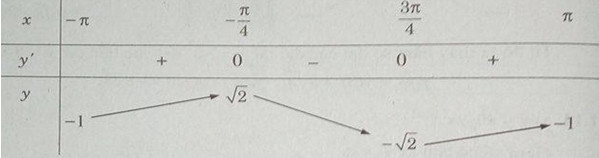
Hàm số đạt cực đại tại \(x =  - {\pi  \over 4} + k2\pi \) , đạt cực tiểu tại \(x = {{3\pi } \over 4} + k2\pi (k \in Z)\) và

 \({y_{CĐ}} = y( - {\pi  \over 4} + k2\pi ) = \sqrt 2\) ;

\({y_{CT}} = y({{3\pi } \over 4} + k2\pi ) =  - \sqrt 2 (k \in Z)\)       

c) Ta có: \(y = {\sin ^2}x = {{1 - \cos 2x} \over 2}\)

Do đó, hàm số đã cho tuần hoàn với chu kỳ \(\pi \). Ta xét hàm số \(y = {1 \over 2} - {1 \over 2}\cos 2x\) trên đoạn \({\rm{[}}0;\pi {\rm{]}}\) .

\(\eqalign{
& y' = \sin 2x \cr 
& y' = 0 < = > \sin 2x = 0 < = > x = k.{\pi \over 2}(k \in Z) \cr} \) 

Lập bảng biến thiên trên đoạn \(\left[ {0,\pi } \right]\)

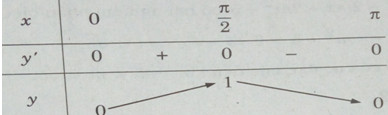
Từ đó, ta thấy hàm số đạt cực tiểu tại \(x = k.{\pi  \over 2}\) với k chẵn, đạt cực đại tại \(x = k.{\pi  \over 2}\) với k lẻ, và  

\({y_{CT}} = y(2m\pi ) = 0;\)

\({y_{CĐ}} = y((2m + 1){\pi  \over 2}) = 1(m \in Z)\)

Bài 1.15 trang 15 Sách bài tập (SBT) Giải tích 12

Xác định giá trị của m để hàm số sau có cực trị:

a) \(y = {x^3} - 3{x^2} + mx - 5\)

b) \(y = {x^3} + 2m{x^2} + mx - 1\)

c) \(y = {{{x^2} - 2mx + 5} \over {x - m}}\)

Hướng dẫn làm bài:

a) TXĐ:  D = R

  \(y' = 3{x^2} - 6x + m\)

Hàm số có cực trị khi và chỉ khi y’ đổi dấu trên R.

⇔ 3x² – 6x + m  có hai nghiệm phân biệt.

⇔ ∆’ = 9 – 3m > 0  ⇔ 3m < 9 ⇔ m < 3.

Vậy hàm số đã cho có cực trị khi m < 3.

b) TXĐ: D = R

y’ = 3x² + 4mx + m

Hàm số có cực trị khi và chỉ khi y’ đổi dấu trên R.

⇔  3x² + 4mx + m có hai nghiệm phân biệt.

⇔ ∆’ = 4m² -3m > 0   ó m(4m – 3) > 0

\( \Leftrightarrow \left[ \matrix{
m < 0 \hfill \cr 
m > {3 \over 4} \hfill \cr} \right.\)

Vậy hàm số đã cho có cực đại, cực tiểu khi m < 0 hoặc \(m > {3 \over 4}\) .

c) TXĐ:  D = R\{m}

\(y' = {{{x^2} - 2mx + 2{m^2} - 5} \over {{{(x - m)}^2}}}\) 

 Hàm số có cực trị khi và chỉ khi y’ đổi dấu trên D

⇔ x² – 2mx + 2m² – 5  có hai nghiệm phân biệt.

⇔  ∆’ = - m² + 5 > 0 ⇔  \( - \sqrt 5  < m < \sqrt 5 \)

Bài 1.16 trang 15 Sách bài tập (SBT) Giải tích 12

Xác định giá trị của tham số m để hàm số y = x³ – 2x² + mx + 1  đạt cực tiểu tại x = 1.

(Đề thi tốt nghiệp THPT năm 2011)

Hướng dẫn làm bài:

TXĐ:  D = R

       y’ = 3x² – 4x + m   ; y’ = 0 ⇔ 3x² – 4x + m = 0

Phương trình trên có hai nghiệm phân biệt khi:

       ∆’ = 4 – 3m   > 0 ⇔ \(m < {4 \over 3}\)             (*)

Hàm số có cực trị tại x = 1 thì :

      y’(1) = 3 – 4 + m = 0  => m = 1  (thỏa mãn điều kiện (*) )

Mặt khác, vì:

       y’’ = 6x – 4    => y’’(1) = 6 – 4 = 2 > 0

cho nên tại x = 1, hàm số đạt cực tiểu.

Vậy với m = 1, hàm số đã cho đạt cực tiểu tại x = 1

Giaibaitap.me